坐标系中的45角问题,方法归纳与总结
文档属性
| 名称 | 坐标系中的45角问题,方法归纳与总结 |
|
|
| 格式 | zip | ||
| 文件大小 | 320.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览


文档简介
坐标系中的45°角,方法归纳总结
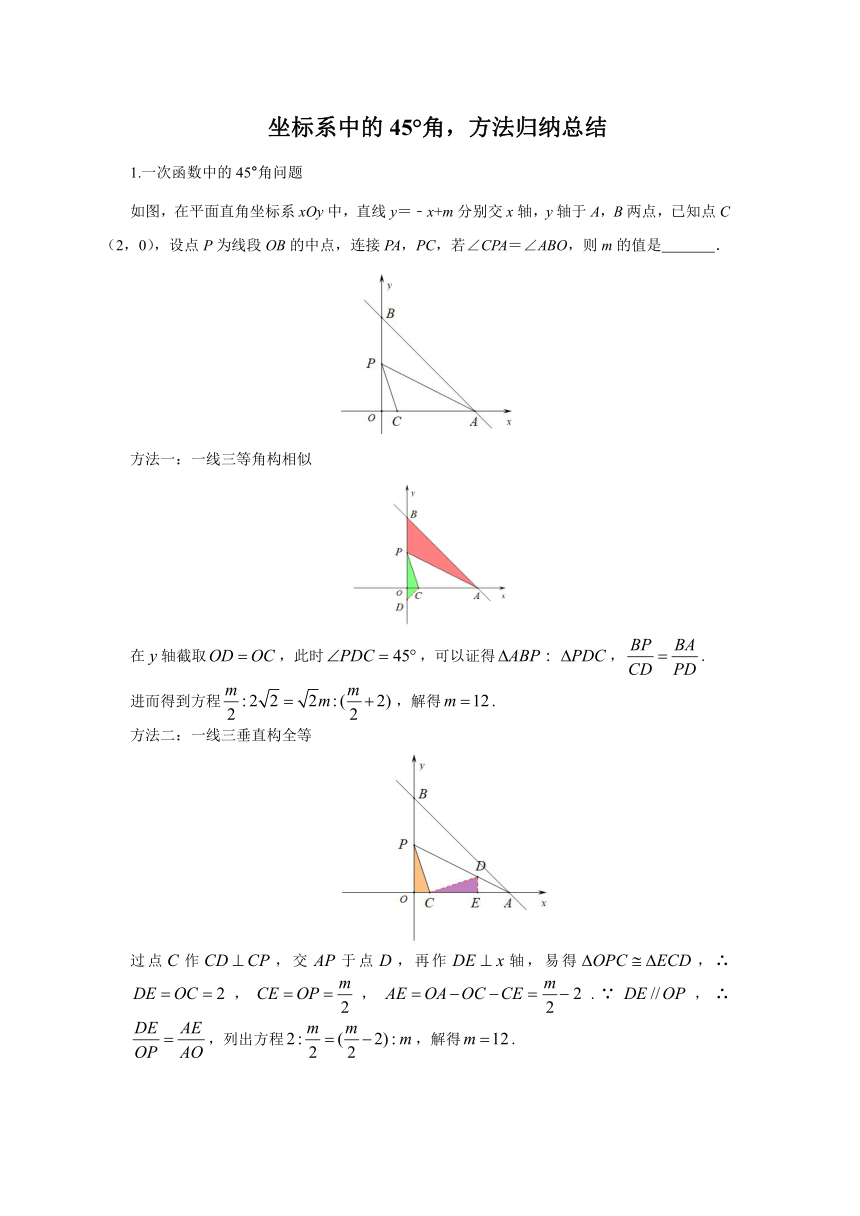
1.一次函数中的45°角问题
如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0),设点P为线段OB的中点,连接PA,PC,若∠CPA=∠ABO,则m的值是 .
方法一:一线三等角构相似
在轴截取,此时,可以证得,.
进而得到方程,解得.
方法二:一线三垂直构全等
过点作,交于点,再作轴,易得,∴,,.∵,∴,列出方程,解得.
方法三:角平分线定理
过点作.∵,所以为的角平分线,∴’
∵,并且求出的坐标,可得,解得.
方法四:半角模型
过点构造正方形.,,根据预备知识得到.又∵,在中有,解得.
方法五:勾股定理
作,可知为等腰直角三角形.由, ,易得,.在中,利用勾股定理,得,解得.
方法六:四点共圆
以为直角边构造等腰直角.∵,所以、、、四点共圆,且以为直径,为圆心.∵,,,
根据,可得,解得.
2.反比例函数中的45°角问题
如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为 .
方法一:构造相似三角形
过点作等腰直角,作,连结,易得,.
设,可以证得,得,∴,解得,∴求出的解析式为,再与联列方程,得到点坐标为.
方法二:
过点作,构造如图所示的辅助线,易得.设的坐标为,可得,.因为点在直线上,可以求得点的坐标为,进而求得,.∵,
∴,列出方程2:,解得(舍去).
所以点的坐标为.
方法三:利用角平分线定理
过点A作AD AB交x轴于点D,由A(2,3)B(0,2)得AB:y=x+2,AD:y=-2x+7得D(,0),F(-4,0),AF=3,AD=,由角平线可知,得E(1,0),AE:y=3x-3得C(-1,-6)
方法四:半角模型
∵,∴,.设点为,则,.利用预备知识,可得.在直角中,,解得,得到.
方法五:直角三角形
作(后面计算可得和重合).设,则,,.又∵,得到,∴,∴.
方法六:共圆
引入过A、F、E三点的圆,设E(a,0)则EF=a+4,H(-4,a+4),G(,),点G在直线y=-x+a,代入可得a=1,即E(1,0)AE:y=3x-3得C(-1,-6)
1.一次函数中的45°角问题
如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0),设点P为线段OB的中点,连接PA,PC,若∠CPA=∠ABO,则m的值是 .
方法一:一线三等角构相似
在轴截取,此时,可以证得,.
进而得到方程,解得.
方法二:一线三垂直构全等
过点作,交于点,再作轴,易得,∴,,.∵,∴,列出方程,解得.
方法三:角平分线定理
过点作.∵,所以为的角平分线,∴’
∵,并且求出的坐标,可得,解得.
方法四:半角模型
过点构造正方形.,,根据预备知识得到.又∵,在中有,解得.
方法五:勾股定理
作,可知为等腰直角三角形.由, ,易得,.在中,利用勾股定理,得,解得.
方法六:四点共圆
以为直角边构造等腰直角.∵,所以、、、四点共圆,且以为直径,为圆心.∵,,,
根据,可得,解得.
2.反比例函数中的45°角问题
如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为 .
方法一:构造相似三角形
过点作等腰直角,作,连结,易得,.
设,可以证得,得,∴,解得,∴求出的解析式为,再与联列方程,得到点坐标为.
方法二:
过点作,构造如图所示的辅助线,易得.设的坐标为,可得,.因为点在直线上,可以求得点的坐标为,进而求得,.∵,
∴,列出方程2:,解得(舍去).
所以点的坐标为.
方法三:利用角平分线定理
过点A作AD AB交x轴于点D,由A(2,3)B(0,2)得AB:y=x+2,AD:y=-2x+7得D(,0),F(-4,0),AF=3,AD=,由角平线可知,得E(1,0),AE:y=3x-3得C(-1,-6)
方法四:半角模型
∵,∴,.设点为,则,.利用预备知识,可得.在直角中,,解得,得到.
方法五:直角三角形
作(后面计算可得和重合).设,则,,.又∵,得到,∴,∴.
方法六:共圆
引入过A、F、E三点的圆,设E(a,0)则EF=a+4,H(-4,a+4),G(,),点G在直线y=-x+a,代入可得a=1,即E(1,0)AE:y=3x-3得C(-1,-6)
