沪科版数学八年级下册 18.1 勾股定理-课件(共29张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理-课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
从一个故事开始…
1955年希腊发行了一张邮票,这张邮票的背后有一段动人的故事,你想听吗?
1955年希腊发行
黑白相间的地砖
毕达哥拉斯(公元前572—前497年),古希腊著名的哲学家、数学家、天文学家.
A
B
A
B
C
C
18.1 勾股定理
s1
s2
s3
a
b
c
探究:如图是行距、列距都是1的方格网
S1、S2、S3的值各是多少?它们之间有什么关系?
图(1)
看一看,想一想
b
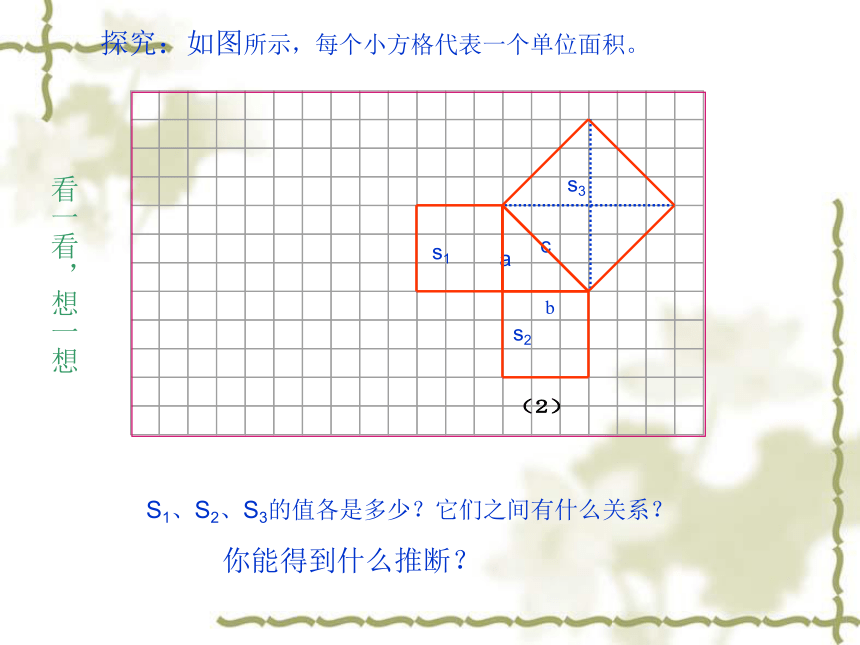
探究:如图所示,每个小方格代表一个单位面积。
S1、S2、S3的值各是多少?它们之间有什么关系?
你能得到什么推断?
a
c
s1
s2
s3
看一看,想一想
A
B
C
S1
S2
S3
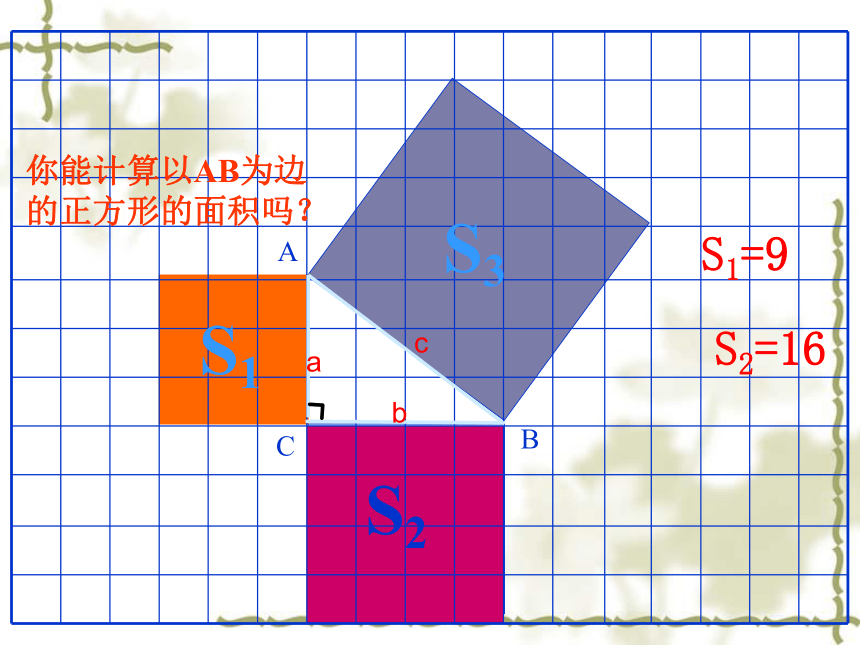
你能计算以AB为边
的正方形的面积吗?
S1=9
S2=16
a
b
c
这是用“补”的方法
A
B
C
s1
s2
s3
S3 =25
这是用“割”的方法
s1
s2
s3
A
B
C
S3 =25
根据上述探究填表
S1的面积(单位 面积) S2的面积(单位 面积) S3的面积(单位 面积)
图1
图2
图3
S1、S2、S3 面积 关系
用直角三角形的边表示
1
1
2
9
9
18
9
16
25
S1+S2=S3
a2+b2=c2
a
c
b
如果直角三角形的两直角边长分别为a、b,
斜边长为c,那么
a2+b2=c2
猜一猜
∟
a
b
c
用这样的四个全等的直角三角形拼一拼、摆一摆,看看是否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?并与同伴交流。
拼一拼
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4× ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 ab/2-(b- a)2
证一证
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4 ab/2
证一证
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理耶!
商高
《周髀算经》
商高定理
勾股史话
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中.
赵爽:东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。
赵爽的这个证明可谓别具匠心,极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系。
勾股史话
刘徽
九章算术
青朱出入图
勾股史话
定理拓展
A
C
B
a 勾
股
c 弦
b
c=
a=
b=
勾股定理:直角三角形两直角边的平方和等于斜边的平方。a2 + b2 = c2
变式:
勾股定理应用注意
1、适用范围(条件):直角三角形。
2、分清直角边与斜边。
A
B
C
a
b
c
几何语言表述: ∵∠C=90
∴a2+b2=c2
例 求出下列直角三角形中未知边的长度
6
8
x
5
x
13
解:(1)由勾股定理得:
x2 =36+64
x2 =100
x2=62+82
x=10
∵ x2+52=132
∴ x2=132-52
x2=169-25
x2=144
x=12
(2)由勾股定理得:
如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
试一试
1. ABC的边a=6,b=8,则c=10 ( )
判断正误
2 .直角三角形ABC中,∠B =90 ,a=3,b=4,那么c=5 ( )
试一试
×
×
5
已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
4
3
A
C
B
4
3
C
A
B
或
试一试
使用勾股定理有哪些要注意的呢?
1、适用范围(条件):直角三角形。
2、分清谁是直角边、谁是斜边,必 要时须分类讨论。
注意:
总结反思,畅谈收获
本节课你有那些收获?
你最感兴趣的地方是什么?
2、(选做)如图,已知四边形ABCD中,∠DAB=∠DBC=90
AD=3,AB=4,DC=13
求:BC的长。
B
C
D
A
第1题图
第2题图
作业
1、(必做)下列阴影部分是一正方形,求此正方形的 面积。
15厘米
17厘米
再见
从一个故事开始…
1955年希腊发行了一张邮票,这张邮票的背后有一段动人的故事,你想听吗?
1955年希腊发行
黑白相间的地砖
毕达哥拉斯(公元前572—前497年),古希腊著名的哲学家、数学家、天文学家.
A
B
A
B
C
C
18.1 勾股定理
s1
s2
s3
a
b
c
探究:如图是行距、列距都是1的方格网
S1、S2、S3的值各是多少?它们之间有什么关系?
图(1)
看一看,想一想
b
探究:如图所示,每个小方格代表一个单位面积。
S1、S2、S3的值各是多少?它们之间有什么关系?
你能得到什么推断?
a
c
s1
s2
s3
看一看,想一想
A
B
C
S1
S2
S3
你能计算以AB为边
的正方形的面积吗?
S1=9
S2=16
a
b
c
这是用“补”的方法
A
B
C
s1
s2
s3
S3 =25
这是用“割”的方法
s1
s2
s3
A
B
C
S3 =25
根据上述探究填表
S1的面积(单位 面积) S2的面积(单位 面积) S3的面积(单位 面积)
图1
图2
图3
S1、S2、S3 面积 关系
用直角三角形的边表示
1
1
2
9
9
18
9
16
25
S1+S2=S3
a2+b2=c2
a
c
b
如果直角三角形的两直角边长分别为a、b,
斜边长为c,那么
a2+b2=c2
猜一猜
∟
a
b
c
用这样的四个全等的直角三角形拼一拼、摆一摆,看看是否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?并与同伴交流。
拼一拼
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4× ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 ab/2-(b- a)2
证一证
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4 ab/2
证一证
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理耶!
商高
《周髀算经》
商高定理
勾股史话
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中.
赵爽:东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。
赵爽的这个证明可谓别具匠心,极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系。
勾股史话
刘徽
九章算术
青朱出入图
勾股史话
定理拓展
A
C
B
a 勾
股
c 弦
b
c=
a=
b=
勾股定理:直角三角形两直角边的平方和等于斜边的平方。a2 + b2 = c2
变式:
勾股定理应用注意
1、适用范围(条件):直角三角形。
2、分清直角边与斜边。
A
B
C
a
b
c
几何语言表述: ∵∠C=90
∴a2+b2=c2
例 求出下列直角三角形中未知边的长度
6
8
x
5
x
13
解:(1)由勾股定理得:
x2 =36+64
x2 =100
x2=62+82
x=10
∵ x2+52=132
∴ x2=132-52
x2=169-25
x2=144
x=12
(2)由勾股定理得:
如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
试一试
1. ABC的边a=6,b=8,则c=10 ( )
判断正误
2 .直角三角形ABC中,∠B =90 ,a=3,b=4,那么c=5 ( )
试一试
×
×
5
已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
4
3
A
C
B
4
3
C
A
B
或
试一试
使用勾股定理有哪些要注意的呢?
1、适用范围(条件):直角三角形。
2、分清谁是直角边、谁是斜边,必 要时须分类讨论。
注意:
总结反思,畅谈收获
本节课你有那些收获?
你最感兴趣的地方是什么?
2、(选做)如图,已知四边形ABCD中,∠DAB=∠DBC=90
AD=3,AB=4,DC=13
求:BC的长。
B
C
D
A
第1题图
第2题图
作业
1、(必做)下列阴影部分是一正方形,求此正方形的 面积。
15厘米
17厘米
再见
