苏教版六年级上学期数学 7整理与复习 课件(共17张PPT)
文档属性
| 名称 | 苏教版六年级上学期数学 7整理与复习 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
整理与复习
应用广角
解决问题的策略
假设
运用数学知识解决生活中的问题
简单的分数乘、除问题的特点:
有一个具体数量和分率,数量与分率对应或数量与问题对应
抓住含有分率的关键句子,确定单位“1”,写出数量关系式,
单位“1”×几分之几=与几分之几对应的数量
比的问题:求出一份的量,数量÷对应的份数=一份的数量
我们常用的长度单位、面积单位、体积单位有哪些?
单位名称 常用的各有哪些单位?相邻两个单位间的进率是多少
长度单位
面积单位
体积单位
千米
米
分米
厘米
毫米
平方千米
平方分米
平方厘米
平方米
公顷
立方米
立方分米
立方厘米
升
毫升
1000
10
10
10
100
10000
100
100
1000
1000
1000
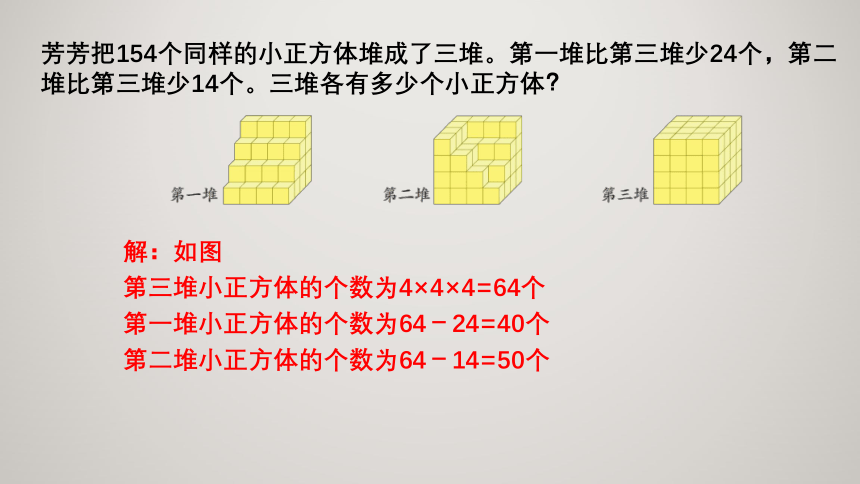
芳芳把154个同样的小正方体堆成了三堆。第一堆比第三堆少24个,第二堆比第三堆少14个。三堆各有多少个小正方体?
解:如图
第三堆小正方体的个数为4×4×4=64个
第一堆小正方体的个数为64-24=40个
第二堆小正方体的个数为64-14=50个
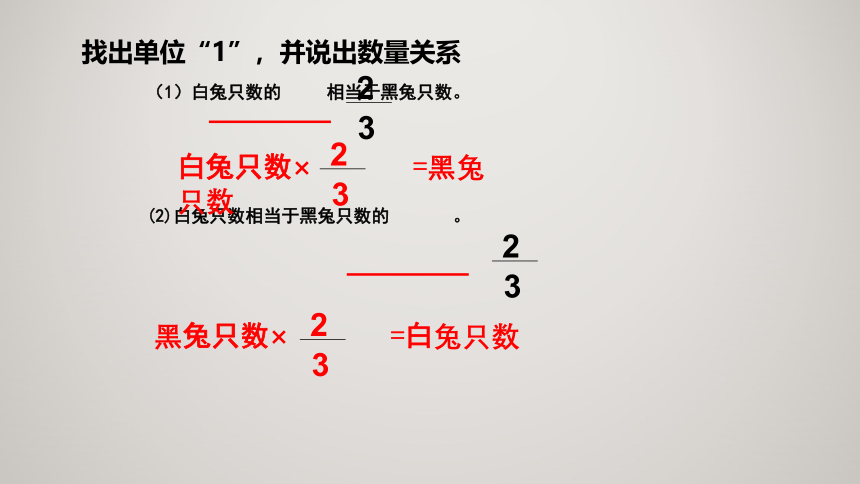
找出单位“1”,并说出数量关系
(1)白兔只数的 相当于黑兔只数。
(2)白兔只数相当于黑兔只数的 。
2
3
2
3
白兔只数
白兔只数× =黑兔只数
2
3
黑兔只数× =白兔只数
2
3
二月份产量比一月份增产 。
一件上衣原来90元,现在降价 。
1
5
1
5
一月份产量× =增产的产量
1
5
上衣原价× =降价的
1
5
(1) 米的 是( )米,
(2) ( )的 是 米,
(3) ( )是 米的 ,
(4) 米是 米的( )
(5) 米的( ) 是 米。
(6) ( )米的 是 米的 。
1
4
1
4
1
4
3
5
1
4
2
3
2
3
2
3
2
5
1
4
2
5
1
4
2
5
1
6
8
3
米
1
6
米
8
5
5
8
1
6
口头列式解答
典型题型:长方体和正方体的体积
思路导引:
这道题可以从不同角度思考。方法一:要求水面上升的高度,就要先求出水面上升部分水的体积,而水面上升部分水的体积就是正方体铁块的体积,用正方体铁块的体积÷长方体玻璃缸的底面积,即可求出水面上升的高度。方法二:正方体铁块放入水中后,水面会上升,水面上升后的高度=(水的体积+正方体铁块的体积)÷长方体玻璃缸的底面积,水的体积可以根据“长方体的体积=长×宽×高(缸内水深)”求出,正方体铁块的体积可以根据体积计算公式求出,长方体玻璃缸的长和宽已知,因此水面上升后的高度就能求出。用水面上升后的高度减去水面原来的高度,就能求出水面上升的高度。
【例题】一个长方体玻璃缸,从里面量时,长9分米,宽4分米,高7分米,缸内水深4分米。如果在水中放入一个棱长是3分米的正方体铁块(水未溢出,且铁块浸没),那么水面上升多少分米?
典型题型:商品销售中的问题
【例题】一种商品第一次降价10%,第二次又降价20%,要想恢复原价,应在第二次降价的基础上提价几分之几?
思路导引:
“第一次降价10%”是把原价看成单位“1”,而“第二次又降价20%”是把第一次降价后的价格看成单位“1”,后来“要想恢复原价”是把第二次降价之后的价格看成单位“1”。
点评苑
本题中涉及的三个单位“1”各不相同,这也是本题在解题过程中最容易出错的地方。其实在降价或提价之后,如果再发生变化,那么都是把降价或提价之后的价格看成单位“1”。
完全解答:
(1-10%)×(1-20%)=72%
(1-72%)÷72%=
答:应在第二次降价的基础上提价 。
(路程÷时间=1分钟行的路程)
(时间÷路程=行1千米要的时间)
×
=
典型题型:长方体(正方体)的底面积、表面积、体积和容积的综合应用特征
【例题】奥体游泳馆新建了一个长方体游泳池,从里面量得长100米,宽80米,高2米。
⑴这个游泳池的占地面积是多少?
⑵建这个游泳池需要挖土多少立方米?
⑶给游泳池的低面和侧面贴瓷砖,如果每平方米瓷砖的价格是30元,那么一共需要多少元?
⑷如果每立方米水重1吨,那么在游泳池中注入多少吨水,才能使水深1.5米?
思路导引:
⑴求这个游泳池的占地面积,就是求长方体的低面积,游泳池的长和宽的积就是长方体的低面积。⑵求建这个游泳池需要挖土多少立方米,就是求游泳池的容积,根据“长方体的容积=长×宽×高”求解。⑶求给游泳池贴瓷砖需要多少元,就要先求出贴瓷砖的面积,也就是长方体的低面积和侧面积的和。再用每平方米瓷砖的价格乘贴瓷砖的面积,就可以求出贴瓷砖一共需要多少钱。⑷求注入水的质量,就要先求出注入水的体积,求注入水的体积要用游泳池的底在面积乘水的深度(不是游泳池的高度),再根据“每立方米的水重1吨”,求出注入水的质量。
典型题型:稍复杂的利润问题
【例题】一种商品按30%的利润率定价,为了提高销量,按定价打八折,结果每件商品仍获利4元。这种商品的成本是多少元?
思路导引:
“按30%的利润率定价”,是把商品的成本看作单位“1”,利润是成本的30%,即定价是成本的1+30%=130%。“按定价打八折”,这时候的定价就是成本的130%×80%=104%,求出此时的利润率,进而求出成本。
点评苑
与利润相关的实际问题,通常成本是一个不变量,可以将它看作单位“1”。观察题目中其它相关量的变化情况,以数量关系“利润=成本×利润率”作为基本关系,找出其中隐藏的其它数量关系进行解答。
完全解答:
1+30%=130%
104%-1=4%
答:这种商品的成本是100元。
130%×80%=104%
4÷4%=100(元)
(1)南门小学买来皮球个数60个,足球个数比皮球多 ,足球比皮球多多少个?
2
5
(2)南门小学买来足球个数比皮球多 ,正好多24个,学校买来皮球多少个?
2
5
对比训练
皮球个数× =足球比皮球多的个数
60× =
2
5
皮球个数× =足球比皮球多的个数
24÷ =
2
5
2
5
2
5
典型题型:比较复杂的表面积问题
【例题】如右图,一个棱长是4厘米的正方体,从正方体上面正中间向下挖一个棱长是2厘米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长是1厘米的正方体小洞,最后得到的物体的表面积是多少平方厘米?
思路导引:
把棱长是1厘米的正方体的底面和棱长是2厘米的正方体的剩余底面合并向上平移,会得到一个完整的面(边长为2厘米的正方形),从而得到一个棱长是4厘米的正方体的表面积(原来边长为4厘米的正方体的表面积);从棱长是4厘米的正方体中挖挖掉两个正方体小洞后,表面积比原来增加了棱长是2厘米的正方体四个侧面与棱长是1厘米的正方体四个侧面的面积之和。
点评苑
从物体中挖去比它更小的图形,表面积的变化是不确定的,计算表面积时,要观察哪些面不变,哪些面在变,又是怎样变化的,找出其中的关系,再解答。
完全解答:
4×4×6+2×2×4+1×1×4=116(平方厘米)
答:最后得到的物体的表面积是116平方厘米.
思维拓展
1.行一段路程,去时用了8小时,回来时少用了2小时,去时比回来慢了百分之几?
2. A、B两种商品的价格比是5:3,如果它们的价格分别下跌30元,它们的价格比是2:1,这两种商品的价格原来各是多少元?
回来用的时间=8-2=6(小时)
8
1
6
1
( — )÷ =25%
6
1
原: A价格:B价格=5:3
后: A价格:B价格=2:1=4:2
差不变
30÷(5-4)=30(元)
30×5=150(元)→A
30×3=90(元)→B
谢谢
整理与复习
应用广角
解决问题的策略
假设
运用数学知识解决生活中的问题
简单的分数乘、除问题的特点:
有一个具体数量和分率,数量与分率对应或数量与问题对应
抓住含有分率的关键句子,确定单位“1”,写出数量关系式,
单位“1”×几分之几=与几分之几对应的数量
比的问题:求出一份的量,数量÷对应的份数=一份的数量
我们常用的长度单位、面积单位、体积单位有哪些?
单位名称 常用的各有哪些单位?相邻两个单位间的进率是多少
长度单位
面积单位
体积单位
千米
米
分米
厘米
毫米
平方千米
平方分米
平方厘米
平方米
公顷
立方米
立方分米
立方厘米
升
毫升
1000
10
10
10
100
10000
100
100
1000
1000
1000
芳芳把154个同样的小正方体堆成了三堆。第一堆比第三堆少24个,第二堆比第三堆少14个。三堆各有多少个小正方体?
解:如图
第三堆小正方体的个数为4×4×4=64个
第一堆小正方体的个数为64-24=40个
第二堆小正方体的个数为64-14=50个
找出单位“1”,并说出数量关系
(1)白兔只数的 相当于黑兔只数。
(2)白兔只数相当于黑兔只数的 。
2
3
2
3
白兔只数
白兔只数× =黑兔只数
2
3
黑兔只数× =白兔只数
2
3
二月份产量比一月份增产 。
一件上衣原来90元,现在降价 。
1
5
1
5
一月份产量× =增产的产量
1
5
上衣原价× =降价的
1
5
(1) 米的 是( )米,
(2) ( )的 是 米,
(3) ( )是 米的 ,
(4) 米是 米的( )
(5) 米的( ) 是 米。
(6) ( )米的 是 米的 。
1
4
1
4
1
4
3
5
1
4
2
3
2
3
2
3
2
5
1
4
2
5
1
4
2
5
1
6
8
3
米
1
6
米
8
5
5
8
1
6
口头列式解答
典型题型:长方体和正方体的体积
思路导引:
这道题可以从不同角度思考。方法一:要求水面上升的高度,就要先求出水面上升部分水的体积,而水面上升部分水的体积就是正方体铁块的体积,用正方体铁块的体积÷长方体玻璃缸的底面积,即可求出水面上升的高度。方法二:正方体铁块放入水中后,水面会上升,水面上升后的高度=(水的体积+正方体铁块的体积)÷长方体玻璃缸的底面积,水的体积可以根据“长方体的体积=长×宽×高(缸内水深)”求出,正方体铁块的体积可以根据体积计算公式求出,长方体玻璃缸的长和宽已知,因此水面上升后的高度就能求出。用水面上升后的高度减去水面原来的高度,就能求出水面上升的高度。
【例题】一个长方体玻璃缸,从里面量时,长9分米,宽4分米,高7分米,缸内水深4分米。如果在水中放入一个棱长是3分米的正方体铁块(水未溢出,且铁块浸没),那么水面上升多少分米?
典型题型:商品销售中的问题
【例题】一种商品第一次降价10%,第二次又降价20%,要想恢复原价,应在第二次降价的基础上提价几分之几?
思路导引:
“第一次降价10%”是把原价看成单位“1”,而“第二次又降价20%”是把第一次降价后的价格看成单位“1”,后来“要想恢复原价”是把第二次降价之后的价格看成单位“1”。
点评苑
本题中涉及的三个单位“1”各不相同,这也是本题在解题过程中最容易出错的地方。其实在降价或提价之后,如果再发生变化,那么都是把降价或提价之后的价格看成单位“1”。
完全解答:
(1-10%)×(1-20%)=72%
(1-72%)÷72%=
答:应在第二次降价的基础上提价 。
(路程÷时间=1分钟行的路程)
(时间÷路程=行1千米要的时间)
×
=
典型题型:长方体(正方体)的底面积、表面积、体积和容积的综合应用特征
【例题】奥体游泳馆新建了一个长方体游泳池,从里面量得长100米,宽80米,高2米。
⑴这个游泳池的占地面积是多少?
⑵建这个游泳池需要挖土多少立方米?
⑶给游泳池的低面和侧面贴瓷砖,如果每平方米瓷砖的价格是30元,那么一共需要多少元?
⑷如果每立方米水重1吨,那么在游泳池中注入多少吨水,才能使水深1.5米?
思路导引:
⑴求这个游泳池的占地面积,就是求长方体的低面积,游泳池的长和宽的积就是长方体的低面积。⑵求建这个游泳池需要挖土多少立方米,就是求游泳池的容积,根据“长方体的容积=长×宽×高”求解。⑶求给游泳池贴瓷砖需要多少元,就要先求出贴瓷砖的面积,也就是长方体的低面积和侧面积的和。再用每平方米瓷砖的价格乘贴瓷砖的面积,就可以求出贴瓷砖一共需要多少钱。⑷求注入水的质量,就要先求出注入水的体积,求注入水的体积要用游泳池的底在面积乘水的深度(不是游泳池的高度),再根据“每立方米的水重1吨”,求出注入水的质量。
典型题型:稍复杂的利润问题
【例题】一种商品按30%的利润率定价,为了提高销量,按定价打八折,结果每件商品仍获利4元。这种商品的成本是多少元?
思路导引:
“按30%的利润率定价”,是把商品的成本看作单位“1”,利润是成本的30%,即定价是成本的1+30%=130%。“按定价打八折”,这时候的定价就是成本的130%×80%=104%,求出此时的利润率,进而求出成本。
点评苑
与利润相关的实际问题,通常成本是一个不变量,可以将它看作单位“1”。观察题目中其它相关量的变化情况,以数量关系“利润=成本×利润率”作为基本关系,找出其中隐藏的其它数量关系进行解答。
完全解答:
1+30%=130%
104%-1=4%
答:这种商品的成本是100元。
130%×80%=104%
4÷4%=100(元)
(1)南门小学买来皮球个数60个,足球个数比皮球多 ,足球比皮球多多少个?
2
5
(2)南门小学买来足球个数比皮球多 ,正好多24个,学校买来皮球多少个?
2
5
对比训练
皮球个数× =足球比皮球多的个数
60× =
2
5
皮球个数× =足球比皮球多的个数
24÷ =
2
5
2
5
2
5
典型题型:比较复杂的表面积问题
【例题】如右图,一个棱长是4厘米的正方体,从正方体上面正中间向下挖一个棱长是2厘米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长是1厘米的正方体小洞,最后得到的物体的表面积是多少平方厘米?
思路导引:
把棱长是1厘米的正方体的底面和棱长是2厘米的正方体的剩余底面合并向上平移,会得到一个完整的面(边长为2厘米的正方形),从而得到一个棱长是4厘米的正方体的表面积(原来边长为4厘米的正方体的表面积);从棱长是4厘米的正方体中挖挖掉两个正方体小洞后,表面积比原来增加了棱长是2厘米的正方体四个侧面与棱长是1厘米的正方体四个侧面的面积之和。
点评苑
从物体中挖去比它更小的图形,表面积的变化是不确定的,计算表面积时,要观察哪些面不变,哪些面在变,又是怎样变化的,找出其中的关系,再解答。
完全解答:
4×4×6+2×2×4+1×1×4=116(平方厘米)
答:最后得到的物体的表面积是116平方厘米.
思维拓展
1.行一段路程,去时用了8小时,回来时少用了2小时,去时比回来慢了百分之几?
2. A、B两种商品的价格比是5:3,如果它们的价格分别下跌30元,它们的价格比是2:1,这两种商品的价格原来各是多少元?
回来用的时间=8-2=6(小时)
8
1
6
1
( — )÷ =25%
6
1
原: A价格:B价格=5:3
后: A价格:B价格=2:1=4:2
差不变
30÷(5-4)=30(元)
30×5=150(元)→A
30×3=90(元)→B
谢谢
