山西省山大附中2012-2013学年高二下学期期中数学理试题
文档属性
| 名称 | 山西省山大附中2012-2013学年高二下学期期中数学理试题 | 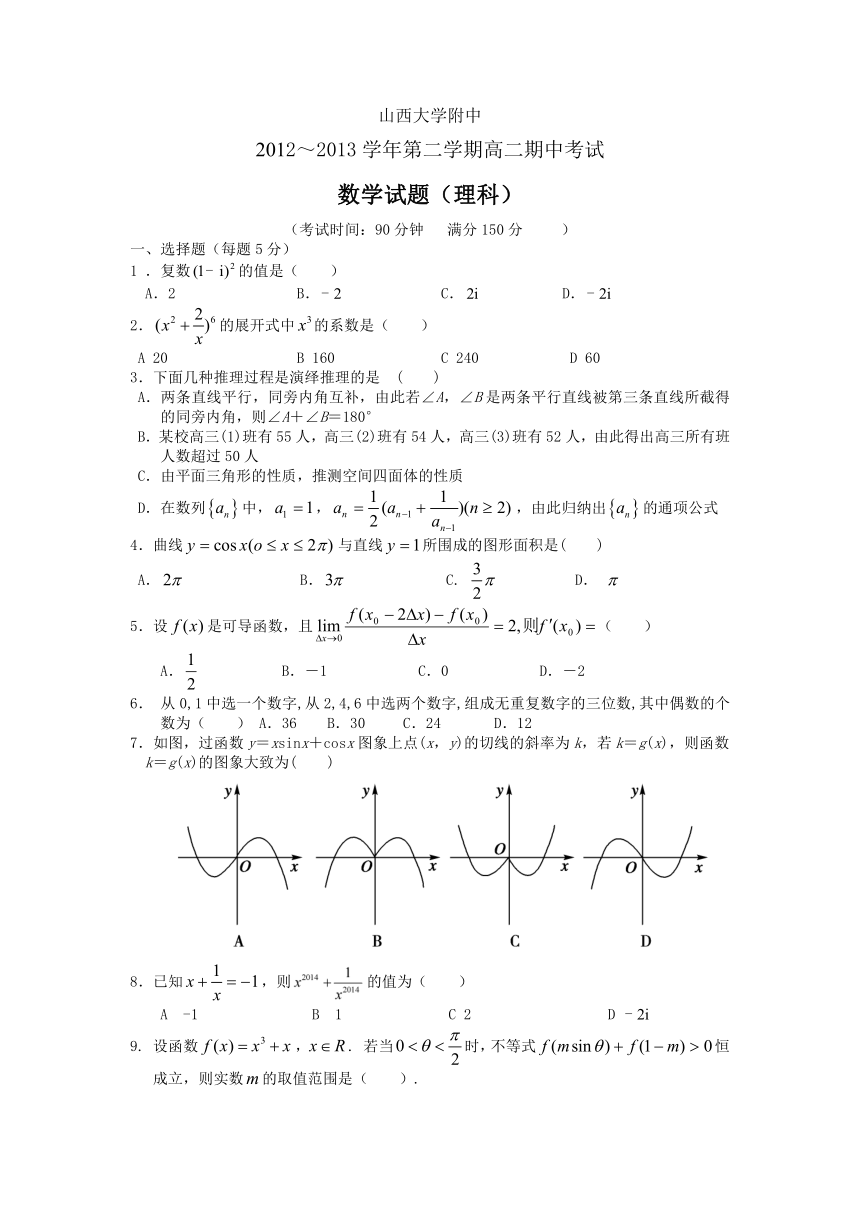 | |
| 格式 | zip | ||
| 文件大小 | 186.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-04 10:19:23 | ||
图片预览




文档简介
山西大学附中
2012~2013学年第二学期高二期中考试
数学试题(理科)
(考试时间:90分钟 满分150分 )
一、选择题(每题5分)
1 .复数的值是( )
A.2 B. C. D.
2.的展开式中的系数是( )
A 20 B 160 C 240 D 60
3.下面几种推理过程是演绎推理的是 ( )
A.两条直线平行,同旁内角互补,由此若∠A,∠B是两条平行直线被第三条直线所截得的同旁内角,则∠A+∠B=180°
B.某校高三(1)班有55人,高三(2)班有54人,高三(3)班有52人,由此得出高三所有班人数超过50人
C.由平面三角形的性质,推测空间四面体的性质
D.在数列中,,,由此归纳出的通项公式
4.曲线与直线所围成的图形面积是( )
A. B. C. D.
5.设是可导函数,且( )
A. B.-1 C.0 D.-2
6. 从0,1中选一个数字,从2,4,6中选两个数字,组成无重复数字的三位数,其中偶数的个数为( ) A.36 B.30 C.24 D.12
7.如图,过函数y=xsinx+cosx图象上点(x,y)的切线的斜率为k,若k=g(x),则函数k=g(x)的图象大致为( )
8.已知,则的值为( )
A -1 B 1 C 2 D
9. 设函数,. 若当时,不等式恒成立,则实数的取值范围是( ).
A. B. C. D.
10.已知f(x)是偶函数,当.x∈[0,]时,f(x)=xsinx,若a =f(cos1),b =f(cos2) ,
c =f(cos3),则 a,b,c 的大小关系为( )
A. a < b < c B. b < a < c C. c < b < a D. b < c < a
11.已知在处取最大值,以下各式正确的序号为( )
① ② ③ ④ ⑤
A.①④ B.②⑤ C.②④ D.③⑤
12. 设函数在上有定义.对于给定的正数,定义函数,取函数.若对于任意的恒有,则 ( )
A. 的最小值为 B. 的最大值为 C.的最小值为2 D.的最大值为2
二、填空题(每题6分)
13.设函数,若,则 .
14.已知的展开式中第三项与第五项的系数之比为,则展开式中常数项是______ .
15.在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数, 那么就称它们为一个逆序.一个排列中逆序的总数就称作这个排列的逆序数.如排列 1,3,5, 4,2中,3,2 ; 5,4 ; 5,2 ; 4,2为逆序,逆序数是4.现有从1?101 这101个自然数的排列:1,3,5,7,…,99 ,101 ,100, 98,…,6,4,2 ,则此排列的逆序数是______ .
16.已知函数,则下列命题正确的是______ .
① ②; ③;
④; ⑤
山西大学附中
2012~2013学年第二学期高二期中考试
数学试题答卷纸(理科)
(考试时间:90分钟 满分150分 命题人:张耀军)
选择题 (每小题5分, 共60 分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每题 6分, 共 24 分)
13. 14.
15. 16.
三、解答题 (共66 分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
(1)计算(6分)
(2)已知复数z1满足(1+i)z 1=-1+5i, z 2=a-2-i, 其中i为虚数单位,a∈R,
若<|z1|,求a的取值范围.(6分)
18.(本小题满分12分)
在一次抽奖活动中,有甲、乙等6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获奖1000元,再从余下的4人中随机抽取1人获奖600元,最后还从这4人中随机抽取1人获奖400元。
(Ⅰ)求甲和乙都不获奖的概率;
(Ⅱ )设X是甲获奖的金额,求X的分布列。
19.(本小题满分12分)
已知数列{}满足+=2n+1
(1)求出,,的值;
(2)由(1)猜想出数列{}的通项公式;并用数学归纳法证明。
20.(本小题满分14分)
已知函数.
(Ⅰ)当时,求函数的单调区间和极值;
(Ⅱ)若在区间上是单调递减函数,求实数的取值范围.
21. (本小题满分16分)
已知函数,且在处的切线方程为
(1)求的解析式;
(2)证明:当时,恒有
(3)证明:若且则
山西大学附中
2012~2013学年第二学期高二期中考试
数学试题参考答案(理科)
(考试时间:90分钟 满分150分 )
一、选择题(每题5分)
1、D 2、B 3、A 4、 A 5、 B 6、C
7、 A 8 、A 9 、A 10、B 11、B 12、A
二、填空题(每题6分)
13、 3 14、 45
15、 2500 16、 ④⑤
三、解答题
17、(满分12分)
解:(1)
………………6分
(2)解:由题意得 z1==2+3i,
于是==,=.
<,
得a2-8a+7<0,118、(满分12分)
解:(Ⅰ)设“甲和乙都不获奖”为事件A , ………………………………1分
则P(A)=,
答:甲和乙都不获奖的概率为. ……………………………………5分
(Ⅱ)X的所有可能的取值为0,400,600,1000,…………………………………6分
P(X=0)=, P(X=400)= , P(X=600)= ,
P(X=1000)= , …………………………………………10分
∴X的分布列为
X
0
400
600
1000
P
……12分
19、(满分12分)
解:(1)=,=,=…………… 3分
(2)猜想= (n)…………5分
证明:(1)当n=1时,显然成立
(2) 假设n=k(k)时成立,即=,……………7分
则当n=k+1时,由
得
化简得
即当n=k+1时亦成立
所以=即对成立。……………12分
20、(满分14分)
解(Ⅰ)函数的定义域为(0,+∞). ………………1分
当时, ……………………3分
当变化时,的变化情况如下:
-
0
+
极小值
21、(满分16分)
解(1),切线斜率,
在处的切线方程为,即 (4分)
(2)令
当时,;时,
故即.(10分)
(3)先求在处的切线方程,由(1)知,
2012~2013学年第二学期高二期中考试
数学试题(理科)
(考试时间:90分钟 满分150分 )
一、选择题(每题5分)
1 .复数的值是( )
A.2 B. C. D.
2.的展开式中的系数是( )
A 20 B 160 C 240 D 60
3.下面几种推理过程是演绎推理的是 ( )
A.两条直线平行,同旁内角互补,由此若∠A,∠B是两条平行直线被第三条直线所截得的同旁内角,则∠A+∠B=180°
B.某校高三(1)班有55人,高三(2)班有54人,高三(3)班有52人,由此得出高三所有班人数超过50人
C.由平面三角形的性质,推测空间四面体的性质
D.在数列中,,,由此归纳出的通项公式
4.曲线与直线所围成的图形面积是( )
A. B. C. D.
5.设是可导函数,且( )
A. B.-1 C.0 D.-2
6. 从0,1中选一个数字,从2,4,6中选两个数字,组成无重复数字的三位数,其中偶数的个数为( ) A.36 B.30 C.24 D.12
7.如图,过函数y=xsinx+cosx图象上点(x,y)的切线的斜率为k,若k=g(x),则函数k=g(x)的图象大致为( )
8.已知,则的值为( )
A -1 B 1 C 2 D
9. 设函数,. 若当时,不等式恒成立,则实数的取值范围是( ).
A. B. C. D.
10.已知f(x)是偶函数,当.x∈[0,]时,f(x)=xsinx,若a =f(cos1),b =f(cos2) ,
c =f(cos3),则 a,b,c 的大小关系为( )
A. a < b < c B. b < a < c C. c < b < a D. b < c < a
11.已知在处取最大值,以下各式正确的序号为( )
① ② ③ ④ ⑤
A.①④ B.②⑤ C.②④ D.③⑤
12. 设函数在上有定义.对于给定的正数,定义函数,取函数.若对于任意的恒有,则 ( )
A. 的最小值为 B. 的最大值为 C.的最小值为2 D.的最大值为2
二、填空题(每题6分)
13.设函数,若,则 .
14.已知的展开式中第三项与第五项的系数之比为,则展开式中常数项是______ .
15.在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数, 那么就称它们为一个逆序.一个排列中逆序的总数就称作这个排列的逆序数.如排列 1,3,5, 4,2中,3,2 ; 5,4 ; 5,2 ; 4,2为逆序,逆序数是4.现有从1?101 这101个自然数的排列:1,3,5,7,…,99 ,101 ,100, 98,…,6,4,2 ,则此排列的逆序数是______ .
16.已知函数,则下列命题正确的是______ .
① ②; ③;
④; ⑤
山西大学附中
2012~2013学年第二学期高二期中考试
数学试题答卷纸(理科)
(考试时间:90分钟 满分150分 命题人:张耀军)
选择题 (每小题5分, 共60 分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每题 6分, 共 24 分)
13. 14.
15. 16.
三、解答题 (共66 分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
(1)计算(6分)
(2)已知复数z1满足(1+i)z 1=-1+5i, z 2=a-2-i, 其中i为虚数单位,a∈R,
若<|z1|,求a的取值范围.(6分)
18.(本小题满分12分)
在一次抽奖活动中,有甲、乙等6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获奖1000元,再从余下的4人中随机抽取1人获奖600元,最后还从这4人中随机抽取1人获奖400元。
(Ⅰ)求甲和乙都不获奖的概率;
(Ⅱ )设X是甲获奖的金额,求X的分布列。
19.(本小题满分12分)
已知数列{}满足+=2n+1
(1)求出,,的值;
(2)由(1)猜想出数列{}的通项公式;并用数学归纳法证明。
20.(本小题满分14分)
已知函数.
(Ⅰ)当时,求函数的单调区间和极值;
(Ⅱ)若在区间上是单调递减函数,求实数的取值范围.
21. (本小题满分16分)
已知函数,且在处的切线方程为
(1)求的解析式;
(2)证明:当时,恒有
(3)证明:若且则
山西大学附中
2012~2013学年第二学期高二期中考试
数学试题参考答案(理科)
(考试时间:90分钟 满分150分 )
一、选择题(每题5分)
1、D 2、B 3、A 4、 A 5、 B 6、C
7、 A 8 、A 9 、A 10、B 11、B 12、A
二、填空题(每题6分)
13、 3 14、 45
15、 2500 16、 ④⑤
三、解答题
17、(满分12分)
解:(1)
………………6分
(2)解:由题意得 z1==2+3i,
于是==,=.
<,
得a2-8a+7<0,1
解:(Ⅰ)设“甲和乙都不获奖”为事件A , ………………………………1分
则P(A)=,
答:甲和乙都不获奖的概率为. ……………………………………5分
(Ⅱ)X的所有可能的取值为0,400,600,1000,…………………………………6分
P(X=0)=, P(X=400)= , P(X=600)= ,
P(X=1000)= , …………………………………………10分
∴X的分布列为
X
0
400
600
1000
P
……12分
19、(满分12分)
解:(1)=,=,=…………… 3分
(2)猜想= (n)…………5分
证明:(1)当n=1时,显然成立
(2) 假设n=k(k)时成立,即=,……………7分
则当n=k+1时,由
得
化简得
即当n=k+1时亦成立
所以=即对成立。……………12分
20、(满分14分)
解(Ⅰ)函数的定义域为(0,+∞). ………………1分
当时, ……………………3分
当变化时,的变化情况如下:
-
0
+
极小值
21、(满分16分)
解(1),切线斜率,
在处的切线方程为,即 (4分)
(2)令
当时,;时,
故即.(10分)
(3)先求在处的切线方程,由(1)知,
同课章节目录
