湖北省2021—2022学年人教版数学八年级下册第18章 平行四边形 期末考试专题练 (word版、含解析)
文档属性
| 名称 | 湖北省2021—2022学年人教版数学八年级下册第18章 平行四边形 期末考试专题练 (word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 17:07:35 | ||
图片预览



文档简介
第18章 平行四边形(1) 期末考试专题练 湖北省2021—2022学年人教版数学八年级下册
一.选择题(共14小题)
1.(2021秋 荆门期末)如图,△ABC的周长为20,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=8,则MN的长度为( )
A. B.2 C. D.3
2.(2021春 黄陂区期末)如图,在 ABCD中,BC=10,AC=8,BD=14,则△AOD的周长是( )
A.16 B.20 C.21 D.23
3.(2021春 广水市期末)如图,四边形ABCD的两条对角线相交于点O,且互相平分,添加下列条件仍不能判定四边形ABCD是菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
4.(2021春 伍家岗区期末)如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A.4 B.8 C.16 D.32
5.(2021春 伍家岗区期末)如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( )
A.6cm2 B.36cm2 C.18cm2 D.2cm2
6.(2021春 来凤县期末)如图,正方形ABCD中,点E在边AD上,点F在边CD上,若∠BEF=∠EBC,AB=3AE,则下列结论:①DF=FC;②AE+DF=EF;③∠BFE=∠BFC;④∠ABE+∠CBF=45°;⑤∠DEF+∠CBF=∠BFC;⑥DF:DE:EF=3:4:5.其中结论正确结论的个数是( )
A.6 B.5 C.4 D.3
7.(2021春 荆门期末)如图,在Rt△ABC中,∠ACB=90°,点G,E,D分别是边AB,BC,CA的中点,若DE+CG=7,则CG的长为( )
A.3 B.3.5 C.4 D.5
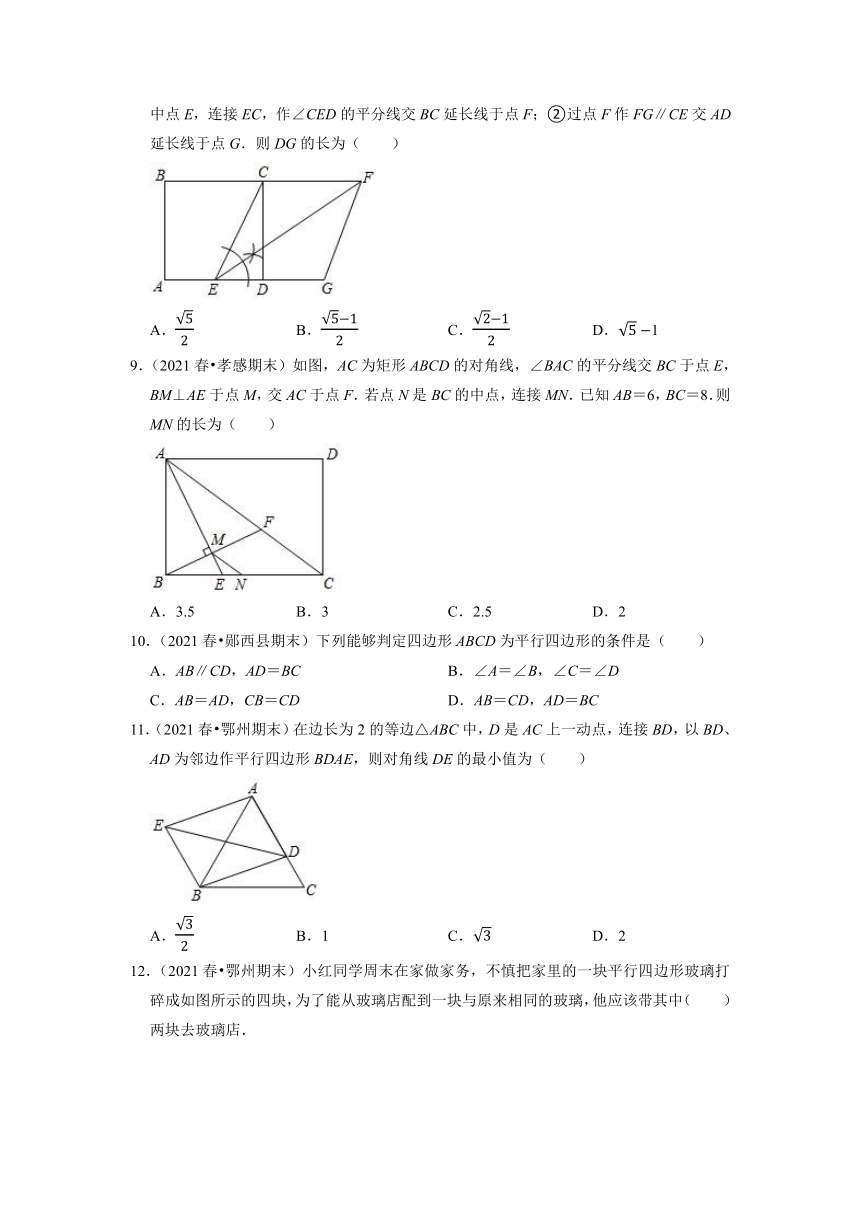
8.(2021春 孝感期末)如图,已知正方形ABCD的边长是1.进行如下操作:①取AD的中点E,连接EC,作∠CED的平分线交BC延长线于点F;②过点F作FG∥CE交AD延长线于点G.则DG的长为( )
A. B. C. D.1
9.(2021春 孝感期末)如图,AC为矩形ABCD的对角线,∠BAC的平分线交BC于点E,BM⊥AE于点M,交AC于点F.若点N是BC的中点,连接MN.已知AB=6,BC=8.则MN的长为( )
A.3.5 B.3 C.2.5 D.2
10.(2021春 郧西县期末)下列能够判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=AD,CB=CD D.AB=CD,AD=BC
11.(2021春 鄂州期末)在边长为2的等边△ABC中,D是AC上一动点,连接BD,以BD、AD为邻边作平行四边形BDAE,则对角线DE的最小值为( )
A. B.1 C. D.2
12.(2021春 鄂州期末)小红同学周末在家做家务,不慎把家里的一块平行四边形玻璃打碎成如图所示的四块,为了能从玻璃店配到一块与原来相同的玻璃,他应该带其中( )两块去玻璃店.
A.①② B.②④ C.②③ D.①③
13.(2021春 宣恩县期末)如图,菱形ABCD的边长是2,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为( )
A. B. C. D.
14.(2021春 咸安区期末)如图,在 ABCD中,AC与BD相交于O,E为CD中点,连接OE,则下列结论不一定成立的是( )
A.BO=DO B.AC=BD
C.OE∥AD且OEAD D.AB=CD
二.填空题(共8小题)
15.(2021春 通山县期末)如图,BD是 ABCD的对角线,点E在BD上,AB=BE=CE,∠A=105°,则∠CBD的大小是 .
16.(2021春 通山县期末)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为8m,则A,B间的距离为 .
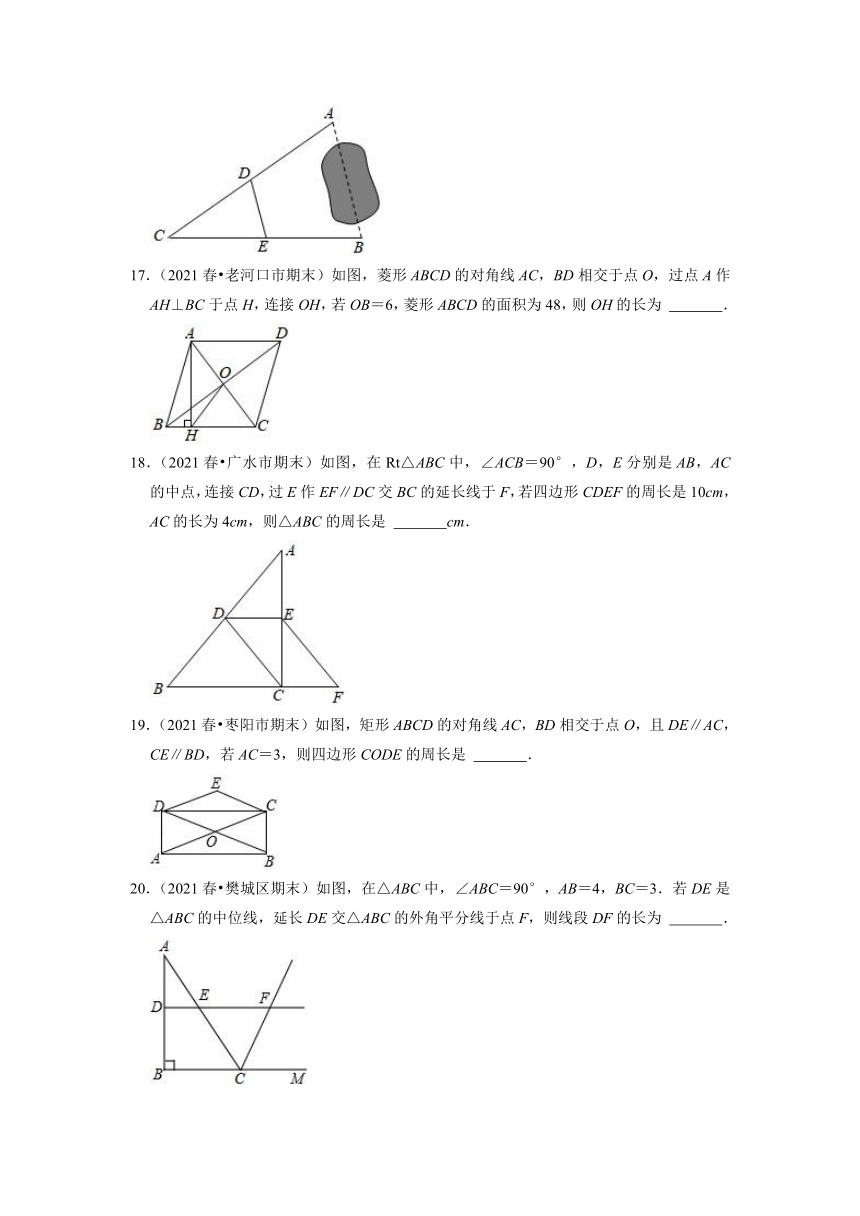
17.(2021春 老河口市期末)如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=6,菱形ABCD的面积为48,则OH的长为 .
18.(2021春 广水市期末)如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,连接CD,过E作EF∥DC交BC的延长线于F,若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是 cm.
19.(2021春 枣阳市期末)如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=3,则四边形CODE的周长是 .
20.(2021春 樊城区期末)如图,在△ABC中,∠ABC=90°,AB=4,BC=3.若DE是△ABC的中位线,延长DE交△ABC的外角平分线于点F,则线段DF的长为 .
21.(2021春 曾都区期末)如图,菱形ABCD的对角线AC,BD交于点O,AC=2,BD=6,将△ABO沿点A到点C的方向平移,得到△A'B'O',当点A'与点C重合时,点A与点B'之间的距离为 .
22.(2021春 十堰期末)如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为 .
三.解答题(共4小题)
23.(2021春 老河口市期末)如图,在 ABCD中,E,F分别是AB,CD的中点,∠BFD=100°.求∠BED的大小.
24.(2021春 黄陂区期末)如图,点O为矩形ABCD对角线的交点,过点D作DE⊥AC于点E,过点B作BF∥AC,交DE的延长线于F,在BF的延长线上取FG=OD,连接AG,OF.
(1)求证:四边形AOFG为菱形;
(2)若AD=5,DF=8,求BG的长.
25.(2021春 枣阳市期末)如图,点A,F,C,D在同一条直线上,点B,E分别在直线AD两侧,且AB=DE,∠A=∠D,AC=DF.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,EF=3,AB=4,当CD为何值时,四边形BCEF是菱形.
26.(2021春 伍家岗区期末)Rt△ABC中,∠ACB=90°,AC=1,AB=3,P为斜边AB上一动点,连接CP,E为CP的中点,连接AE并延长至点F,使EF=AE,连接PF交BC于点G,连接CF.
(1)求证:四边形ACFP为平行四边形;
(2)连接FB,求点P运动至何处时,CP∥BF?并求此时四边形ABFC的周长.
第18章 平行四边形(1) 期末考试专题练 湖北省2021—2022学年人教版数学八年级下册
参考答案与试题解析
一.选择题(共14小题)
1.【解答】解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA)
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∴DE=BE+CD﹣BC=BA+CA﹣BC=20﹣8﹣8=4,
∵AN=NE,AM=MD,
∴MNDE=2,
故选:B.
2.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD=10,AO=COAC=4,BO=DOBD=7,
∴△AOD的周长是:AD+AO+DO=10+4+7=21,
故选:C.
3.【解答】解:∵四边形ABCD的两条对角线相交于点O,且互相平分,
∴四边形ABCD是平行四边形,
∴AD∥BC,
当AB=AD或AC⊥BD时,均可判定四边形ABCD是菱形;
当AC=BD时,可判定四边形ABCD是矩形;
当∠ABD=∠CBD时,
由AD∥BC得:∠CBD=∠ADB,
∴∠ABD=∠ADB,
∴AB=AD,
∴四边形ABCD是菱形;
故选:C.
4.【解答】解:∵四边形ABCD是正方形,
∴∠BDC=45°,
∴EG=DG,
∵四边形EFCG为矩形,
∴EF=GC,
∴EF+EG=GC+DG=DC=4,
故选:A.
5.【解答】解:如图所示:
∵△ABE是直角三角形,AE=8cm,BE=10cm,
∴AB(cm),
∵四边形ABCD是正方形,
∴正方形ABCD的面积=AB2=36(cm2),
故选:B.
6.【解答】解:如图,过点B作BH⊥EF于H.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=∠ABC=90°,AB=AD=CD=BC,AD∥CB,
∴∠AEB=∠EBC,
∵∠FEB=∠EBC,
∴∠AEB=∠BEF,
∵BA⊥AE,BH⊥EF,
∴AB=BH=BC,
∵∠A=∠BHE=∠BHF=∠C=90°,BE=BE,BF=BF,
∴Rt△ABE≌Rt△HBE(HL),Rt△BFH≌Rt△BFC(HL),
∴AE=EH,FH=CF,∠BFE=∠BFC,故③正确,
∴AE+CF=EH+HF=EF,
∴∠ABE=∠HBE,∠FBH=∠FBC,
∴∠ABE+∠CBF=45°,故④正确,
∵∠DEF+∠AEH=180°,∠AEH+∠ABH=180°,
∴∠DEF=∠ABH,
∴∠DEF+∠FBC=∠ABH+∠FBH=∠ABF,
∵AB∥CD,
∴∠ABF=∠BFC,
∴∠DEF+∠CBF=∠BFC,故⑤正确,
∵AB=3AE,
∴可以假设AE=a,则AB=AD=CD=3a,DE=2a,设DF=x,则FH=CF=3a﹣x,EF=a+3a﹣x=4a﹣x,
∵EF2=DE2+DF2,
∴(4a﹣x)2=(2a)2+x2
解得xa,
∴DF=CF,故①正确,
∴AE+DF=EF,故②正确,
∴DFa,DE=2a,EFa,
∴DF:DE:EF=3:4:5,故⑥正确.
故选:A.
7.【解答】解:在Rt△ABC中,∠ACB=90°,点G是边AB的中点,
∴CGAB,
∵点E,D分别是边BC,CA的中点,
∴DE是△ABC的中位线,
∴DEAB,
∴DE=CG,
∵DE+CG=7,
∴CG=DE=3.5,
故选:B.
8.【解答】解:∵四边形ABCD为正方形,
∴∠CDE=90°,BC∥AD,
∴∠CFE=∠FEG,
∵FG∥EC,
∴四边形EGFC为平行四边形,
∵EF平分∠CEG,
∴∠CEF=∠FEG,
∴∠CEF=∠CFE,
∴CE=CF,
∴ EGFC为菱形,
∴CE=EG,
∵E为AD中点,
∴ED,
在Rt△CDE中,由勾股定理得,
CE,
∴EG,
∴DG,
故选:B.
9.【解答】解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=6,BC=8,
∴AC,
∵∠BAC的平分线交BC于点E,BM⊥AE于点M,
∴△ABF是等腰三角形,
∴BM=MF,AB=AF,
∴FC=AC﹣AF=AC﹣AB=10﹣6=4,
∵点N是BC的中点,
∴MN是△BFC的中位线,
∴2MN=FC=4,
∴MN=2,
故选:D.
10.【解答】解:如图所示:
A、∵AB∥CD,AD=BC,不符合“一组对边平行且相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
B、∵∠A=∠B,∠C=∠D,不符合“两组对角分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
C、∵AB=AD,CB=CD,不符合“两组对边分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
D、∵AB=CD,AD=BC,符合“两组对边分别相等的四边形是平行四边形”,
∴四边形ABCD是平行四边形,故本选项符合题意,
故选:D.
11.【解答】解:如图,AB与DE相交于点O,
在△ABC中,∠BAC=60°,
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB.
∴当OD取最小值时,线段DE最短,此时OD⊥AC.
∵点O是AB的中点,
∴OAAB=1,
∵∠ODA=90°,OA=1,∠BAC=60°,
∴OD,
∴ED=2OD,
故选:C.
12.【解答】解:只有②④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②④两块碎玻璃,就可以确定平行四边形的大小.
故选:B.
13.【解答】解:∵四边形ABCD是菱形,
∴AD=AB=2,
∵E是AB的中点,
∴AE=EB=1,
∵DE⊥AB,
∴∠AED=90°
在Rt△ADE中,DE,
∴菱形ABCD的面积=AB DE=22,
故选:B.
14.【解答】解:∵四边形ABCD是平行四边形,AC与BD相交于O,E为CD中点,
∴BO=DO,AB=CD,故A,D正确;
∴OE∥AD,且OEAD,故C正确;
故选:B.
二.填空题(共8小题)
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠BCD=105°,
∵AB=BE=CE,
∴BE=EC=CD,
∴∠DBC=∠BCE,∠CED=∠CDE,
∴∠CED=∠CDE=2∠DBC,
∵∠DBC+∠BDC+∠BCD=180°,
∴∠DBC+2∠DBC+105°=180°,
∴∠DBC=25°,
故答案为:25°.
16.【解答】解:∵点D,E是AC,BC的中点,DE=8m,
∴AB=2DE=16(m),
故答案为:16m.
17.【解答】解:∵ABCD是菱形,
∴BO=DO=6,AO=CO,S菱形ABCD,
∴AC=8,
∵AH⊥BC,AO=CO=4,
∴OHAC=4.
故答案为:4.
18.【解答】解:∵D,E分别是AB,AC的中点,
∴DEBC,DE∥BC,
∵EF∥DC,
∴四边形CDEF为平行四边形,
∵四边形CDEF的周长是10cm,
∴DE+CD=5cm,
在Rt△ABC中,D是AB的中点,
∴CDAB,
∴AB+BC=2(DE+CD)=10cm,
∵AC的长为4cm,
∴△ABC的周长=AB+BC+AC=14(cm),
故答案为:14.
19.【解答】解:∵四边形ABCD是矩形,AC=3,
∴AO=BO=CO=DOAC,
∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∴四边形ODEC是菱形,
∴OD=DE=CE=OC,
∴四边形CODE的周长=4OC=6,
故答案为:6.
20.【解答】解:在△ABC中,∠ABC=90°,AB=4,BC=3,由勾股定理得到:AC5,
∵DE是△ABC的中位线,
∴DEBC=1.5,DE∥BC,ECAC=2.5,
∴∠EFC=∠FCM,
∵CF是∠ACM的平分线,
∴∠ECF=∠FCM,
∴∠EFC=∠ECF,
∴EF=EC=2.5,
∴DF=DE+EF=1.5+2.5=4,
故答案是:4.
21.【解答】解:连接AB',如图所示:
∵四边形ABCD是菱形,AC=2,BD=6,
∴AC⊥BD,AO=OCAC,OB=ODBD=3,
∵△ABO沿点A到点C的方向平移,得到△A'B'O',点A'与点C重合,
∴O'C=OA,O'B'=OB=3,∠CO'B'=90°,
∴AO'=AC+O'C=3,
∴AB'3,
故答案为:.
22.【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=55°,
∴∠OAB=∠DAB﹣∠OAD=35°,
故答案为:35°.
三.解答题(共4小题)
23.【解答】解:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∵E,F分别是AB,CD的中点,
∴BEAB,DFCD,
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∴∠BED=∠BFD=100°.
24.【解答】证明:(1)∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵DE⊥AC,BF∥AC,
∴OF=OD=OA,
∵FG=OD,
∴FG=OA,
∵FG∥OA,
∴四边形AOFG为菱形;
(2)∵AD=5,DF=8,
∴DE=EF=4,AE=3,
在Rt△DEO中,设OE=x,由勾股定理得:(x+3)2﹣42=x2,
解得:x,
∴OD,OE,
∴BF=2OE,FG=OD,
∴BG=GF+BF.
25.【解答】解:(1)在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形;
(2)当时,四边形BCEF是菱形.
理由如下:
连接BE,交CF与点H,
∵AC=DF,
∴AC﹣FC=DF﹣FC,
即AF=CD,
若四边形BCEF是菱形时,
∴BE⊥CF,,EF=BC=3.
在Rt△ABC中,AB=4,BC=3,
∴.
∵,
即.
在Rt△BCH中,,BC=3,
∴.
∴,
∴,
∴当时,四边形BCEF是菱形.
26.【解答】(1)证明:∵E为CP的中点,
∴CE=PE,
∵EF=AE,
∴四边形ACFP为平行四边形;
(2)解:点P运动至AB的中点时,CP∥BF,理由如下:
由(1)得:四边形ACFP为平行四边形,
∴CF∥AP,CF=AP,
∵点P是AB的中点,
∴BP=AP,
∴CF=BP,
∴四边形BPCF是平行四边形,
∴CP∥BF,BF=CP,
∵∠ACB=90°,P是AB的中点,
∴CPAB=BP=AP,
∴CF=BF,
∴四边形ABFC的周长=AB+AC+CF+BF=3+17.
一.选择题(共14小题)
1.(2021秋 荆门期末)如图,△ABC的周长为20,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=8,则MN的长度为( )
A. B.2 C. D.3
2.(2021春 黄陂区期末)如图,在 ABCD中,BC=10,AC=8,BD=14,则△AOD的周长是( )
A.16 B.20 C.21 D.23
3.(2021春 广水市期末)如图,四边形ABCD的两条对角线相交于点O,且互相平分,添加下列条件仍不能判定四边形ABCD是菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
4.(2021春 伍家岗区期末)如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A.4 B.8 C.16 D.32
5.(2021春 伍家岗区期末)如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( )
A.6cm2 B.36cm2 C.18cm2 D.2cm2
6.(2021春 来凤县期末)如图,正方形ABCD中,点E在边AD上,点F在边CD上,若∠BEF=∠EBC,AB=3AE,则下列结论:①DF=FC;②AE+DF=EF;③∠BFE=∠BFC;④∠ABE+∠CBF=45°;⑤∠DEF+∠CBF=∠BFC;⑥DF:DE:EF=3:4:5.其中结论正确结论的个数是( )
A.6 B.5 C.4 D.3
7.(2021春 荆门期末)如图,在Rt△ABC中,∠ACB=90°,点G,E,D分别是边AB,BC,CA的中点,若DE+CG=7,则CG的长为( )
A.3 B.3.5 C.4 D.5
8.(2021春 孝感期末)如图,已知正方形ABCD的边长是1.进行如下操作:①取AD的中点E,连接EC,作∠CED的平分线交BC延长线于点F;②过点F作FG∥CE交AD延长线于点G.则DG的长为( )
A. B. C. D.1
9.(2021春 孝感期末)如图,AC为矩形ABCD的对角线,∠BAC的平分线交BC于点E,BM⊥AE于点M,交AC于点F.若点N是BC的中点,连接MN.已知AB=6,BC=8.则MN的长为( )
A.3.5 B.3 C.2.5 D.2
10.(2021春 郧西县期末)下列能够判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=AD,CB=CD D.AB=CD,AD=BC
11.(2021春 鄂州期末)在边长为2的等边△ABC中,D是AC上一动点,连接BD,以BD、AD为邻边作平行四边形BDAE,则对角线DE的最小值为( )
A. B.1 C. D.2
12.(2021春 鄂州期末)小红同学周末在家做家务,不慎把家里的一块平行四边形玻璃打碎成如图所示的四块,为了能从玻璃店配到一块与原来相同的玻璃,他应该带其中( )两块去玻璃店.
A.①② B.②④ C.②③ D.①③
13.(2021春 宣恩县期末)如图,菱形ABCD的边长是2,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为( )
A. B. C. D.
14.(2021春 咸安区期末)如图,在 ABCD中,AC与BD相交于O,E为CD中点,连接OE,则下列结论不一定成立的是( )
A.BO=DO B.AC=BD
C.OE∥AD且OEAD D.AB=CD
二.填空题(共8小题)
15.(2021春 通山县期末)如图,BD是 ABCD的对角线,点E在BD上,AB=BE=CE,∠A=105°,则∠CBD的大小是 .
16.(2021春 通山县期末)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为8m,则A,B间的距离为 .
17.(2021春 老河口市期末)如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=6,菱形ABCD的面积为48,则OH的长为 .
18.(2021春 广水市期末)如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,连接CD,过E作EF∥DC交BC的延长线于F,若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是 cm.
19.(2021春 枣阳市期末)如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=3,则四边形CODE的周长是 .
20.(2021春 樊城区期末)如图,在△ABC中,∠ABC=90°,AB=4,BC=3.若DE是△ABC的中位线,延长DE交△ABC的外角平分线于点F,则线段DF的长为 .
21.(2021春 曾都区期末)如图,菱形ABCD的对角线AC,BD交于点O,AC=2,BD=6,将△ABO沿点A到点C的方向平移,得到△A'B'O',当点A'与点C重合时,点A与点B'之间的距离为 .
22.(2021春 十堰期末)如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为 .
三.解答题(共4小题)
23.(2021春 老河口市期末)如图,在 ABCD中,E,F分别是AB,CD的中点,∠BFD=100°.求∠BED的大小.
24.(2021春 黄陂区期末)如图,点O为矩形ABCD对角线的交点,过点D作DE⊥AC于点E,过点B作BF∥AC,交DE的延长线于F,在BF的延长线上取FG=OD,连接AG,OF.
(1)求证:四边形AOFG为菱形;
(2)若AD=5,DF=8,求BG的长.
25.(2021春 枣阳市期末)如图,点A,F,C,D在同一条直线上,点B,E分别在直线AD两侧,且AB=DE,∠A=∠D,AC=DF.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,EF=3,AB=4,当CD为何值时,四边形BCEF是菱形.
26.(2021春 伍家岗区期末)Rt△ABC中,∠ACB=90°,AC=1,AB=3,P为斜边AB上一动点,连接CP,E为CP的中点,连接AE并延长至点F,使EF=AE,连接PF交BC于点G,连接CF.
(1)求证:四边形ACFP为平行四边形;
(2)连接FB,求点P运动至何处时,CP∥BF?并求此时四边形ABFC的周长.
第18章 平行四边形(1) 期末考试专题练 湖北省2021—2022学年人教版数学八年级下册
参考答案与试题解析
一.选择题(共14小题)
1.【解答】解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA)
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∴DE=BE+CD﹣BC=BA+CA﹣BC=20﹣8﹣8=4,
∵AN=NE,AM=MD,
∴MNDE=2,
故选:B.
2.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD=10,AO=COAC=4,BO=DOBD=7,
∴△AOD的周长是:AD+AO+DO=10+4+7=21,
故选:C.
3.【解答】解:∵四边形ABCD的两条对角线相交于点O,且互相平分,
∴四边形ABCD是平行四边形,
∴AD∥BC,
当AB=AD或AC⊥BD时,均可判定四边形ABCD是菱形;
当AC=BD时,可判定四边形ABCD是矩形;
当∠ABD=∠CBD时,
由AD∥BC得:∠CBD=∠ADB,
∴∠ABD=∠ADB,
∴AB=AD,
∴四边形ABCD是菱形;
故选:C.
4.【解答】解:∵四边形ABCD是正方形,
∴∠BDC=45°,
∴EG=DG,
∵四边形EFCG为矩形,
∴EF=GC,
∴EF+EG=GC+DG=DC=4,
故选:A.
5.【解答】解:如图所示:
∵△ABE是直角三角形,AE=8cm,BE=10cm,
∴AB(cm),
∵四边形ABCD是正方形,
∴正方形ABCD的面积=AB2=36(cm2),
故选:B.
6.【解答】解:如图,过点B作BH⊥EF于H.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=∠ABC=90°,AB=AD=CD=BC,AD∥CB,
∴∠AEB=∠EBC,
∵∠FEB=∠EBC,
∴∠AEB=∠BEF,
∵BA⊥AE,BH⊥EF,
∴AB=BH=BC,
∵∠A=∠BHE=∠BHF=∠C=90°,BE=BE,BF=BF,
∴Rt△ABE≌Rt△HBE(HL),Rt△BFH≌Rt△BFC(HL),
∴AE=EH,FH=CF,∠BFE=∠BFC,故③正确,
∴AE+CF=EH+HF=EF,
∴∠ABE=∠HBE,∠FBH=∠FBC,
∴∠ABE+∠CBF=45°,故④正确,
∵∠DEF+∠AEH=180°,∠AEH+∠ABH=180°,
∴∠DEF=∠ABH,
∴∠DEF+∠FBC=∠ABH+∠FBH=∠ABF,
∵AB∥CD,
∴∠ABF=∠BFC,
∴∠DEF+∠CBF=∠BFC,故⑤正确,
∵AB=3AE,
∴可以假设AE=a,则AB=AD=CD=3a,DE=2a,设DF=x,则FH=CF=3a﹣x,EF=a+3a﹣x=4a﹣x,
∵EF2=DE2+DF2,
∴(4a﹣x)2=(2a)2+x2
解得xa,
∴DF=CF,故①正确,
∴AE+DF=EF,故②正确,
∴DFa,DE=2a,EFa,
∴DF:DE:EF=3:4:5,故⑥正确.
故选:A.
7.【解答】解:在Rt△ABC中,∠ACB=90°,点G是边AB的中点,
∴CGAB,
∵点E,D分别是边BC,CA的中点,
∴DE是△ABC的中位线,
∴DEAB,
∴DE=CG,
∵DE+CG=7,
∴CG=DE=3.5,
故选:B.
8.【解答】解:∵四边形ABCD为正方形,
∴∠CDE=90°,BC∥AD,
∴∠CFE=∠FEG,
∵FG∥EC,
∴四边形EGFC为平行四边形,
∵EF平分∠CEG,
∴∠CEF=∠FEG,
∴∠CEF=∠CFE,
∴CE=CF,
∴ EGFC为菱形,
∴CE=EG,
∵E为AD中点,
∴ED,
在Rt△CDE中,由勾股定理得,
CE,
∴EG,
∴DG,
故选:B.
9.【解答】解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=6,BC=8,
∴AC,
∵∠BAC的平分线交BC于点E,BM⊥AE于点M,
∴△ABF是等腰三角形,
∴BM=MF,AB=AF,
∴FC=AC﹣AF=AC﹣AB=10﹣6=4,
∵点N是BC的中点,
∴MN是△BFC的中位线,
∴2MN=FC=4,
∴MN=2,
故选:D.
10.【解答】解:如图所示:
A、∵AB∥CD,AD=BC,不符合“一组对边平行且相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
B、∵∠A=∠B,∠C=∠D,不符合“两组对角分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
C、∵AB=AD,CB=CD,不符合“两组对边分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
D、∵AB=CD,AD=BC,符合“两组对边分别相等的四边形是平行四边形”,
∴四边形ABCD是平行四边形,故本选项符合题意,
故选:D.
11.【解答】解:如图,AB与DE相交于点O,
在△ABC中,∠BAC=60°,
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB.
∴当OD取最小值时,线段DE最短,此时OD⊥AC.
∵点O是AB的中点,
∴OAAB=1,
∵∠ODA=90°,OA=1,∠BAC=60°,
∴OD,
∴ED=2OD,
故选:C.
12.【解答】解:只有②④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②④两块碎玻璃,就可以确定平行四边形的大小.
故选:B.
13.【解答】解:∵四边形ABCD是菱形,
∴AD=AB=2,
∵E是AB的中点,
∴AE=EB=1,
∵DE⊥AB,
∴∠AED=90°
在Rt△ADE中,DE,
∴菱形ABCD的面积=AB DE=22,
故选:B.
14.【解答】解:∵四边形ABCD是平行四边形,AC与BD相交于O,E为CD中点,
∴BO=DO,AB=CD,故A,D正确;
∴OE∥AD,且OEAD,故C正确;
故选:B.
二.填空题(共8小题)
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠BCD=105°,
∵AB=BE=CE,
∴BE=EC=CD,
∴∠DBC=∠BCE,∠CED=∠CDE,
∴∠CED=∠CDE=2∠DBC,
∵∠DBC+∠BDC+∠BCD=180°,
∴∠DBC+2∠DBC+105°=180°,
∴∠DBC=25°,
故答案为:25°.
16.【解答】解:∵点D,E是AC,BC的中点,DE=8m,
∴AB=2DE=16(m),
故答案为:16m.
17.【解答】解:∵ABCD是菱形,
∴BO=DO=6,AO=CO,S菱形ABCD,
∴AC=8,
∵AH⊥BC,AO=CO=4,
∴OHAC=4.
故答案为:4.
18.【解答】解:∵D,E分别是AB,AC的中点,
∴DEBC,DE∥BC,
∵EF∥DC,
∴四边形CDEF为平行四边形,
∵四边形CDEF的周长是10cm,
∴DE+CD=5cm,
在Rt△ABC中,D是AB的中点,
∴CDAB,
∴AB+BC=2(DE+CD)=10cm,
∵AC的长为4cm,
∴△ABC的周长=AB+BC+AC=14(cm),
故答案为:14.
19.【解答】解:∵四边形ABCD是矩形,AC=3,
∴AO=BO=CO=DOAC,
∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∴四边形ODEC是菱形,
∴OD=DE=CE=OC,
∴四边形CODE的周长=4OC=6,
故答案为:6.
20.【解答】解:在△ABC中,∠ABC=90°,AB=4,BC=3,由勾股定理得到:AC5,
∵DE是△ABC的中位线,
∴DEBC=1.5,DE∥BC,ECAC=2.5,
∴∠EFC=∠FCM,
∵CF是∠ACM的平分线,
∴∠ECF=∠FCM,
∴∠EFC=∠ECF,
∴EF=EC=2.5,
∴DF=DE+EF=1.5+2.5=4,
故答案是:4.
21.【解答】解:连接AB',如图所示:
∵四边形ABCD是菱形,AC=2,BD=6,
∴AC⊥BD,AO=OCAC,OB=ODBD=3,
∵△ABO沿点A到点C的方向平移,得到△A'B'O',点A'与点C重合,
∴O'C=OA,O'B'=OB=3,∠CO'B'=90°,
∴AO'=AC+O'C=3,
∴AB'3,
故答案为:.
22.【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=55°,
∴∠OAB=∠DAB﹣∠OAD=35°,
故答案为:35°.
三.解答题(共4小题)
23.【解答】解:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∵E,F分别是AB,CD的中点,
∴BEAB,DFCD,
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∴∠BED=∠BFD=100°.
24.【解答】证明:(1)∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵DE⊥AC,BF∥AC,
∴OF=OD=OA,
∵FG=OD,
∴FG=OA,
∵FG∥OA,
∴四边形AOFG为菱形;
(2)∵AD=5,DF=8,
∴DE=EF=4,AE=3,
在Rt△DEO中,设OE=x,由勾股定理得:(x+3)2﹣42=x2,
解得:x,
∴OD,OE,
∴BF=2OE,FG=OD,
∴BG=GF+BF.
25.【解答】解:(1)在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形;
(2)当时,四边形BCEF是菱形.
理由如下:
连接BE,交CF与点H,
∵AC=DF,
∴AC﹣FC=DF﹣FC,
即AF=CD,
若四边形BCEF是菱形时,
∴BE⊥CF,,EF=BC=3.
在Rt△ABC中,AB=4,BC=3,
∴.
∵,
即.
在Rt△BCH中,,BC=3,
∴.
∴,
∴,
∴当时,四边形BCEF是菱形.
26.【解答】(1)证明:∵E为CP的中点,
∴CE=PE,
∵EF=AE,
∴四边形ACFP为平行四边形;
(2)解:点P运动至AB的中点时,CP∥BF,理由如下:
由(1)得:四边形ACFP为平行四边形,
∴CF∥AP,CF=AP,
∵点P是AB的中点,
∴BP=AP,
∴CF=BP,
∴四边形BPCF是平行四边形,
∴CP∥BF,BF=CP,
∵∠ACB=90°,P是AB的中点,
∴CPAB=BP=AP,
∴CF=BF,
∴四边形ABFC的周长=AB+AC+CF+BF=3+17.
