青岛版(六三)数学六年级下册 用不同的策略解决“鸡兔同笼”问题课件(24张ppt)
文档属性
| 名称 | 青岛版(六三)数学六年级下册 用不同的策略解决“鸡兔同笼”问题课件(24张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 18:43:46 | ||
图片预览






文档简介
(共25张PPT)
用不同的策略解决
“鸡兔同笼”问题
1、结合生活情境,在运用一一列举策略解决问题的过程中,发现规律并学会运用假设的策略解决问题,建立数学模型。
2、经历探索、交流、反思、建模、运用的数学学习过程,体验不同的解决策略的价值,培养创新意识。
3、在积极参与解决问题的过程中,进一步积累解决问题的经验,体验获得成功的乐趣,树立自信心。
学习目标
一个停车场里停有四轮小汽车和两轮摩托车共24辆,这些车共有86个轮子。
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
小汽车4个轮
摩托车2个轮
共86个轮
停车场里有几辆小汽车和几辆摩托车?
共24辆车
情景导入
停车场里有几辆小汽车和几辆摩托车?
探索新知
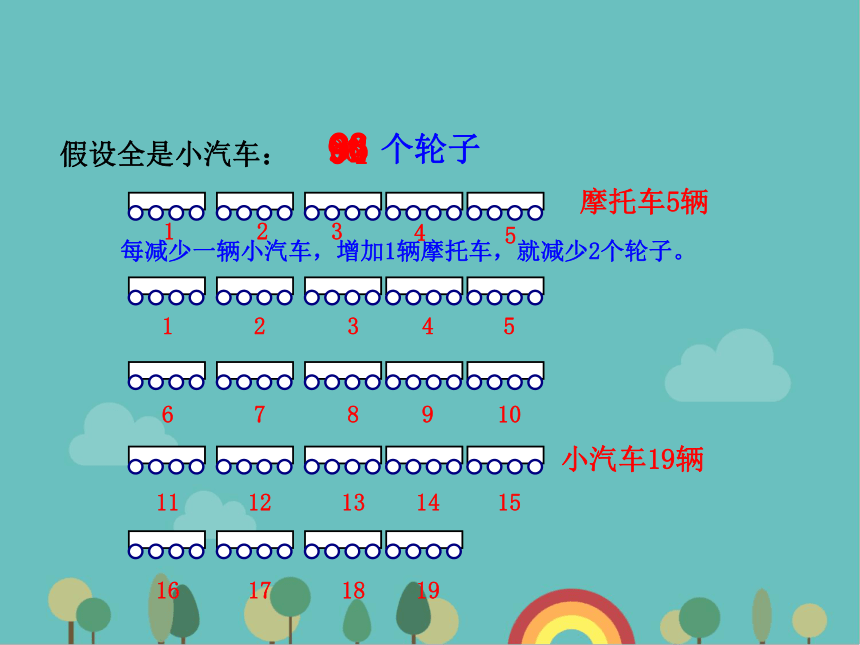
用画图的方法试一试。
车体用长方形表示,车轮用圆表示。
96
94
92
90
88
86
每减少一辆小汽车,增加1辆摩托车,就减少2个轮子。
假设全是小汽车:
摩托车5辆
小汽车19辆
1
2
3
4
5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
个轮子
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
82
84
86
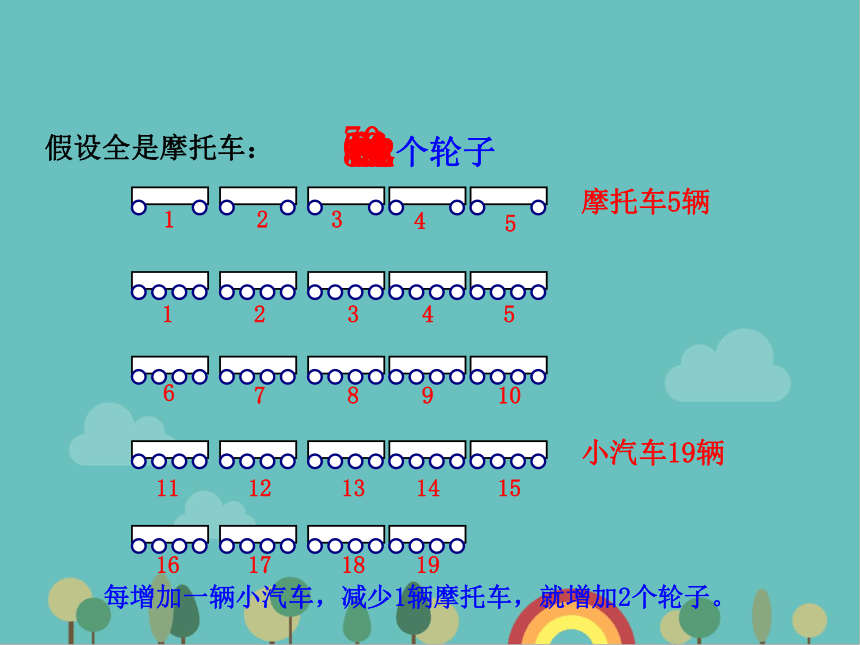
每增加一辆小汽车,减少1辆摩托车,就增加2个轮子。
假设全是摩托车:
个轮子
摩托车5辆
小汽车19辆
1
2
3
4
5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
轮子数
摩托车数
小汽车数
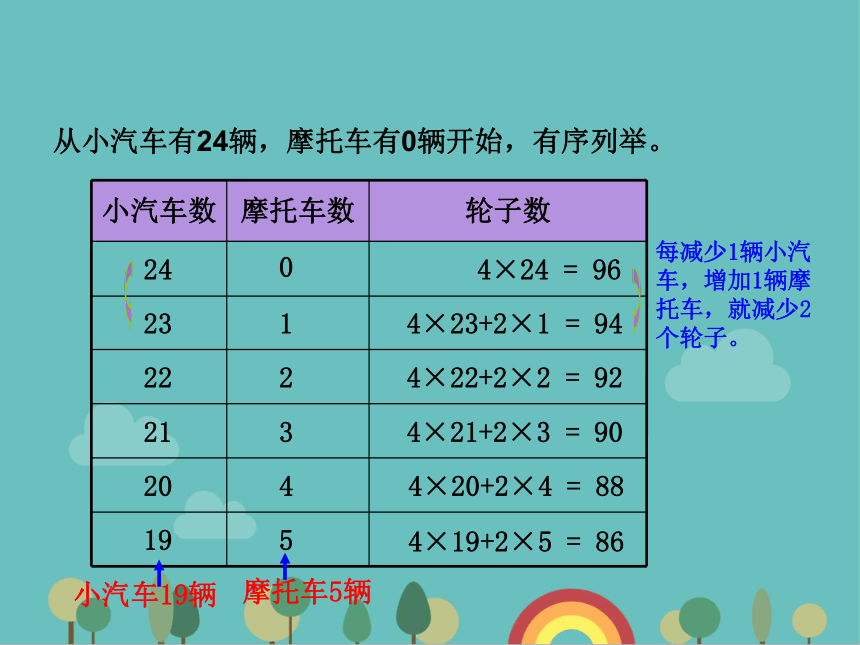
用列举的方法试一试。
轮子数
摩托车数
小汽车数
24
23
22
21
20
19
1
0
2
3
4
5
4×24 = 96
4×23+2×1 = 94
4×22+2×2 = 92
4×21+2×3 = 90
4×20+2×4 = 88
4×19+2×5 = 86
每减少1辆小汽车,增加1辆摩托车,就减少2个轮子。
从小汽车有24辆,摩托车有0辆开始,有序列举。
摩托车5辆
小汽车19辆
0
1
2
3
…
23
24
22
21
…
2×24=48
4×1+2×23=50
4×2+2×22=52
4×3+2×21=54
…
每增加1辆小汽车,减少1辆摩托车,就增加2个轮子。
轮子数
摩托车数
小汽车数
19
5
4×19+2×5=86
从小汽车有0辆,摩托车有24辆开始,有序列举。
摩托车5辆
小汽车19辆
12
13
14
15
…
11
12
10
9
…
4×12+2×12=72
4×13+2×11=74
4×14+2×10=76
4×15+2× 9=78
…
轮子数
摩托车数
小汽车数
19
5
4×19+2×5=86
从小汽车和摩托车各有一半开始,有序列举。
每增加1辆小汽车,减少1辆摩托车,就增加2个轮子。
摩托车5辆
小汽车19辆
用假设的方法试一试。
答:有19辆小汽车和5辆摩托车。
96- 86=10(个)
4 × 24 = 96(个)
4-2=2(个)
10÷2=5(辆)
24-5=19(辆)
假设全部是小汽车。
每辆小汽车有4个轮子,因为都看作是小汽车,轮子总数应是:
比实际多算的轮子数是:
每辆小汽车比摩托车多的轮子数:
每辆摩托车多算2个轮子,所以摩托车的辆数是:
小汽车的辆数是:
列综合算式是:
(4×24-86)÷(4-2)
= (96-86)÷2
= 10 ÷ 2
= 5(辆)
24-5 = 19(辆)
答:有19辆小汽车和5辆摩托车。
86-48 = 38(个)
2 × 24 = 48(个)
4-2=2(个)
38÷2 = 19(辆)
24-19 = 5(辆)
假设全部是摩托车。
每辆摩托车有2个轮子,因为都看作是摩托车,轮子总数应是:
比实际少算的轮子数是:
每辆小汽车比摩托车多的轮子数:
每辆小汽车少算了2个轮子,所以小汽车的辆数是:
摩托车的辆数是:
列综合算式是:
(86-2×24)÷(4-2)
= (86-48)÷2
= 38÷2
= 19(辆)
24-19 = 5( 辆)
列举法
画图法
假设法
想一想,以上我们是怎样一步步解决问题的?
假设
比较
调整
归纳
1.
一只蛐蛐6条腿,一只蜘蛛8条腿。现有蛐蛐和蜘蛛共10只,共有68条腿。蛐蛐和蜘蛛各有几只?
80-68 = 12(条)
8×10 = 80(条)
8-6 = 2(条)
12÷2 = 6(只)
10-6 = 4(只)
答:蛐蛐有6只,蜘蛛有4只。
68-60 = 8(条)
6×10 = 60(条)
8-6 = 2(条)
8÷2 = 4(只)
10-4 = 6(只)
假设10只全是蜘蛛。
假设10只全是蛐蛐。
蛐蛐:
蜘蛛:
蛐蛐:
蜘蛛:
典题精讲
2.
100-82 = 18(元)
5×20 = 100(元)
5-2 = 3(元)
18÷3 = 6(张)
20-6 = 14(张)
答:5元的人民币有14张,2元的有6张。
82-40 =42(元)
2×20 = 40(元)
5-2 = 3(元)
42÷3 = 14(张)
20-14 = 6(张)
王丽有20张5元和2元的人民币,面值一共是82元。5元和2元的人民币各有多少张?
2元:
5元:
2元:
5元:
假设20张全是5元的。
假设20张全是2元的。
安全知识竞赛中共有20道题,每答对一道得5分,答错一道倒扣2分。王亮做了所有的题,共得了79分,他做对了几道题?
答:他做对了13道题。
假设所有的题全做对,得分:20×5=100(分)
实际相差的分数:100-79=21(分)
每做错一道相差的分数:5-2=3(分)
做错的题数:21÷3=7(道)
做对的题数:20-7=13(道)
误区
易错提醒
安全知识竞赛中共有20道题,每答对一道得5分,答错一道倒扣2分。王亮做了所有的题,共得了79分,他做对了几道题?
错解分析:此题错在答对和答错一道题相差的分数不是3分,而是5+2=7(分)。
错解改正:假设所有的题全做对。
做错的题数:(20×5-79)÷(5+2)
=(100-79)÷7
=21÷7
=3(道)
做对的题数:20-3=17(道)
答:他做对了17道题。
安全知识竞赛中共有20道题,每答对一道得5分,答错一道扣2分。王亮做了所有的题,共得了79分,他做对了几道题?
在用“假设法”解答“鸡兔同笼”类型的问题时,要注意假设前后两个数量之间的相差数,有时相差数是两数之和,有时相差数是两数之差。
1.
答:学生票有20张,成人票有30张。
学校买来50张电影票,一部分是4元一张的学生票,一部分是6元一张的成人票,总票价是260元。两种票各买了多少张?
(6×50 - 260)÷(4-2)
= (300 -260)÷2
= 40 ÷ 2
= 20(张)
50-20 = 30(张)
(260 - 4×50)÷(4-2)
= (260 -200)÷2
= 60÷ 2
= 30(张)
50-30 = 20(张)
假设50张票全是6元一张的。
假设50张票全是4元一张的。
4元:
6元:
6元:
4元:
学以致用
2.
答:有14把椅子和4个凳子。
(4×18 - 68)÷(4-3)
= (72 -68)÷1
= 4 ÷ 1
= 4(个)
18-4 = 14(把)
(68 - 3×18)÷(4-3)
= (68 -54)÷1
= 14÷ 1
= 14(把)
18-14 = 4(个)
一个房间里有4条腿的椅子和3条腿的凳子共18个。如果椅子腿和凳子腿加起来共有68条,那么有几把椅子和几个凳子?
凳子:
假设18个全是椅子的。
椅子:
假设18个全是凳子的。
凳子:
椅子:
3.
“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这是我国古代数学著作《孙子算经》中的一道题目,把它翻译成现代汉语是:现在有一些鸡和兔子被关在同一个笼子里,鸡和兔共35个头、94只脚。问鸡和兔各有多少只?
答:鸡有23只,兔子有12只。
(4×35 - 94)÷(4-2)
= (140 -94)÷2
= 46÷ 2
= 23(只)
35-23 =12(只)
假设35只全是兔子。
兔子:
鸡:
画图、列举、假设都是解决问题的有效策略。
分析和解决同一个问题,可以用不同的策略。
要学会根据具体问题,灵活选择策略。
课堂小结
用不同的策略解决
“鸡兔同笼”问题
1、结合生活情境,在运用一一列举策略解决问题的过程中,发现规律并学会运用假设的策略解决问题,建立数学模型。
2、经历探索、交流、反思、建模、运用的数学学习过程,体验不同的解决策略的价值,培养创新意识。
3、在积极参与解决问题的过程中,进一步积累解决问题的经验,体验获得成功的乐趣,树立自信心。
学习目标
一个停车场里停有四轮小汽车和两轮摩托车共24辆,这些车共有86个轮子。
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
小汽车4个轮
摩托车2个轮
共86个轮
停车场里有几辆小汽车和几辆摩托车?
共24辆车
情景导入
停车场里有几辆小汽车和几辆摩托车?
探索新知
用画图的方法试一试。
车体用长方形表示,车轮用圆表示。
96
94
92
90
88
86
每减少一辆小汽车,增加1辆摩托车,就减少2个轮子。
假设全是小汽车:
摩托车5辆
小汽车19辆
1
2
3
4
5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
个轮子
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
82
84
86
每增加一辆小汽车,减少1辆摩托车,就增加2个轮子。
假设全是摩托车:
个轮子
摩托车5辆
小汽车19辆
1
2
3
4
5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
轮子数
摩托车数
小汽车数
用列举的方法试一试。
轮子数
摩托车数
小汽车数
24
23
22
21
20
19
1
0
2
3
4
5
4×24 = 96
4×23+2×1 = 94
4×22+2×2 = 92
4×21+2×3 = 90
4×20+2×4 = 88
4×19+2×5 = 86
每减少1辆小汽车,增加1辆摩托车,就减少2个轮子。
从小汽车有24辆,摩托车有0辆开始,有序列举。
摩托车5辆
小汽车19辆
0
1
2
3
…
23
24
22
21
…
2×24=48
4×1+2×23=50
4×2+2×22=52
4×3+2×21=54
…
每增加1辆小汽车,减少1辆摩托车,就增加2个轮子。
轮子数
摩托车数
小汽车数
19
5
4×19+2×5=86
从小汽车有0辆,摩托车有24辆开始,有序列举。
摩托车5辆
小汽车19辆
12
13
14
15
…
11
12
10
9
…
4×12+2×12=72
4×13+2×11=74
4×14+2×10=76
4×15+2× 9=78
…
轮子数
摩托车数
小汽车数
19
5
4×19+2×5=86
从小汽车和摩托车各有一半开始,有序列举。
每增加1辆小汽车,减少1辆摩托车,就增加2个轮子。
摩托车5辆
小汽车19辆
用假设的方法试一试。
答:有19辆小汽车和5辆摩托车。
96- 86=10(个)
4 × 24 = 96(个)
4-2=2(个)
10÷2=5(辆)
24-5=19(辆)
假设全部是小汽车。
每辆小汽车有4个轮子,因为都看作是小汽车,轮子总数应是:
比实际多算的轮子数是:
每辆小汽车比摩托车多的轮子数:
每辆摩托车多算2个轮子,所以摩托车的辆数是:
小汽车的辆数是:
列综合算式是:
(4×24-86)÷(4-2)
= (96-86)÷2
= 10 ÷ 2
= 5(辆)
24-5 = 19(辆)
答:有19辆小汽车和5辆摩托车。
86-48 = 38(个)
2 × 24 = 48(个)
4-2=2(个)
38÷2 = 19(辆)
24-19 = 5(辆)
假设全部是摩托车。
每辆摩托车有2个轮子,因为都看作是摩托车,轮子总数应是:
比实际少算的轮子数是:
每辆小汽车比摩托车多的轮子数:
每辆小汽车少算了2个轮子,所以小汽车的辆数是:
摩托车的辆数是:
列综合算式是:
(86-2×24)÷(4-2)
= (86-48)÷2
= 38÷2
= 19(辆)
24-19 = 5( 辆)
列举法
画图法
假设法
想一想,以上我们是怎样一步步解决问题的?
假设
比较
调整
归纳
1.
一只蛐蛐6条腿,一只蜘蛛8条腿。现有蛐蛐和蜘蛛共10只,共有68条腿。蛐蛐和蜘蛛各有几只?
80-68 = 12(条)
8×10 = 80(条)
8-6 = 2(条)
12÷2 = 6(只)
10-6 = 4(只)
答:蛐蛐有6只,蜘蛛有4只。
68-60 = 8(条)
6×10 = 60(条)
8-6 = 2(条)
8÷2 = 4(只)
10-4 = 6(只)
假设10只全是蜘蛛。
假设10只全是蛐蛐。
蛐蛐:
蜘蛛:
蛐蛐:
蜘蛛:
典题精讲
2.
100-82 = 18(元)
5×20 = 100(元)
5-2 = 3(元)
18÷3 = 6(张)
20-6 = 14(张)
答:5元的人民币有14张,2元的有6张。
82-40 =42(元)
2×20 = 40(元)
5-2 = 3(元)
42÷3 = 14(张)
20-14 = 6(张)
王丽有20张5元和2元的人民币,面值一共是82元。5元和2元的人民币各有多少张?
2元:
5元:
2元:
5元:
假设20张全是5元的。
假设20张全是2元的。
安全知识竞赛中共有20道题,每答对一道得5分,答错一道倒扣2分。王亮做了所有的题,共得了79分,他做对了几道题?
答:他做对了13道题。
假设所有的题全做对,得分:20×5=100(分)
实际相差的分数:100-79=21(分)
每做错一道相差的分数:5-2=3(分)
做错的题数:21÷3=7(道)
做对的题数:20-7=13(道)
误区
易错提醒
安全知识竞赛中共有20道题,每答对一道得5分,答错一道倒扣2分。王亮做了所有的题,共得了79分,他做对了几道题?
错解分析:此题错在答对和答错一道题相差的分数不是3分,而是5+2=7(分)。
错解改正:假设所有的题全做对。
做错的题数:(20×5-79)÷(5+2)
=(100-79)÷7
=21÷7
=3(道)
做对的题数:20-3=17(道)
答:他做对了17道题。
安全知识竞赛中共有20道题,每答对一道得5分,答错一道扣2分。王亮做了所有的题,共得了79分,他做对了几道题?
在用“假设法”解答“鸡兔同笼”类型的问题时,要注意假设前后两个数量之间的相差数,有时相差数是两数之和,有时相差数是两数之差。
1.
答:学生票有20张,成人票有30张。
学校买来50张电影票,一部分是4元一张的学生票,一部分是6元一张的成人票,总票价是260元。两种票各买了多少张?
(6×50 - 260)÷(4-2)
= (300 -260)÷2
= 40 ÷ 2
= 20(张)
50-20 = 30(张)
(260 - 4×50)÷(4-2)
= (260 -200)÷2
= 60÷ 2
= 30(张)
50-30 = 20(张)
假设50张票全是6元一张的。
假设50张票全是4元一张的。
4元:
6元:
6元:
4元:
学以致用
2.
答:有14把椅子和4个凳子。
(4×18 - 68)÷(4-3)
= (72 -68)÷1
= 4 ÷ 1
= 4(个)
18-4 = 14(把)
(68 - 3×18)÷(4-3)
= (68 -54)÷1
= 14÷ 1
= 14(把)
18-14 = 4(个)
一个房间里有4条腿的椅子和3条腿的凳子共18个。如果椅子腿和凳子腿加起来共有68条,那么有几把椅子和几个凳子?
凳子:
假设18个全是椅子的。
椅子:
假设18个全是凳子的。
凳子:
椅子:
3.
“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这是我国古代数学著作《孙子算经》中的一道题目,把它翻译成现代汉语是:现在有一些鸡和兔子被关在同一个笼子里,鸡和兔共35个头、94只脚。问鸡和兔各有多少只?
答:鸡有23只,兔子有12只。
(4×35 - 94)÷(4-2)
= (140 -94)÷2
= 46÷ 2
= 23(只)
35-23 =12(只)
假设35只全是兔子。
兔子:
鸡:
画图、列举、假设都是解决问题的有效策略。
分析和解决同一个问题,可以用不同的策略。
要学会根据具体问题,灵活选择策略。
课堂小结
