第四章 三角形单元检测题(含答案)
文档属性
| 名称 | 第四章 三角形单元检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 770.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 21:01:15 | ||
图片预览


文档简介
《第四章 三角形》章末复习
一、选择题
1.长度分别为的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4
B.5
C.6
D.7
2.在中,若,则是( )
A.等边三角形
B.锐角三角形
C.直角三角形
D.钝角三角形
3.下列说法中正确的是( )
A.面积相等的两个图形是全等图形
B.周长相等的两个图形是全等图形
C.所有正方形都是全等图形
D.能够完全重合的两个图形是全等图形
4.有四根长度分别为(为正整数)的木棒,从中任取三根,首尾顺次相接,都能组成一个三角形,则组成的三角形的周长( )
A.最小值是11
B.最小值是12
C.最大值是14
D.最大值是15
5.已知是的三边长,且,那么( )
A.
B.
C.
D.不能确定
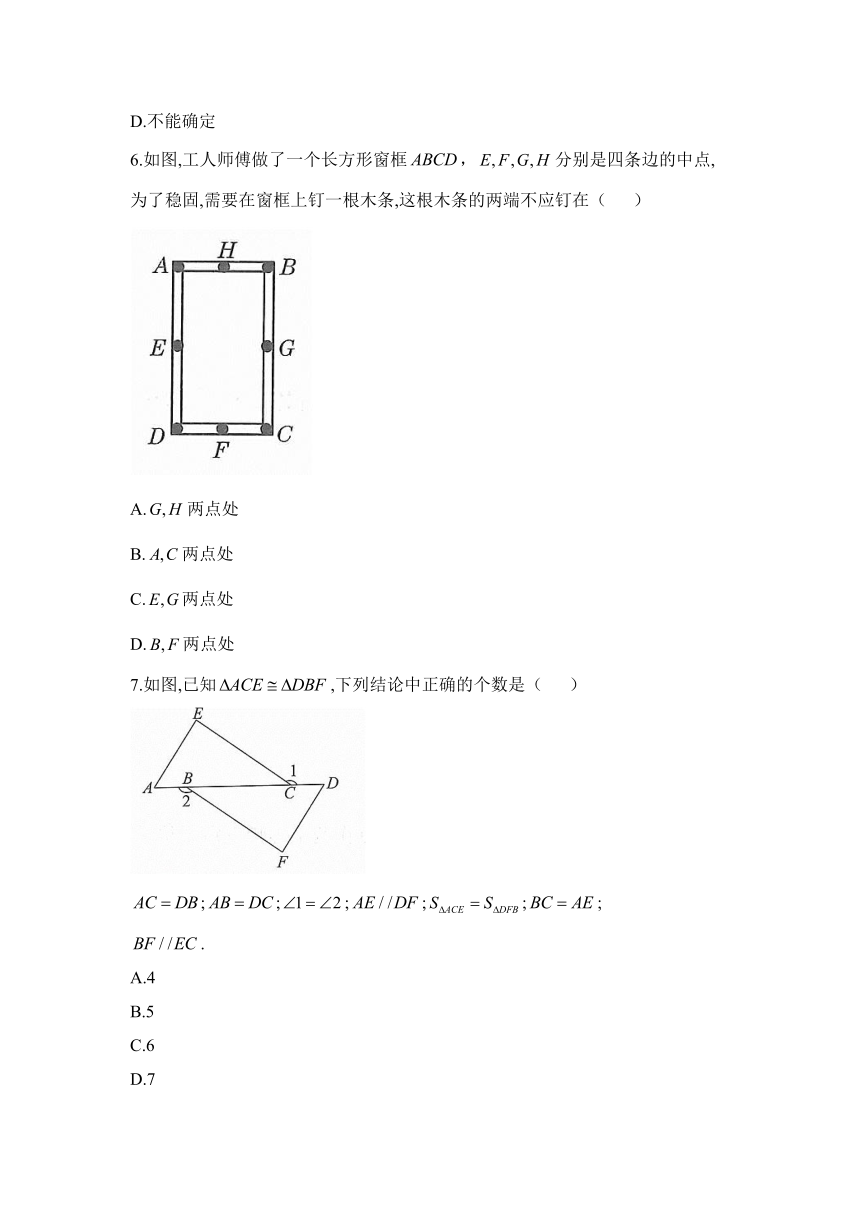
6.如图,工人师傅做了一个长方形窗框,分别是四条边的中点,为了稳固,需要在窗框上钉一根木条,这根木条的两端不应钉在( )
A.两点处
B.两点处
C.两点处
D.两点处
7.如图,已知,下列结论中正确的个数是( )
;;;;;;
.
A.4
B.5
C.6
D.7
8.如图,,则不一定能使的条件是( )
A.
B.
C.
D.
9.在和中,已知条件:;;;
;;.下列各组条件中不能判定的是( )
A.①②③
B.②③④
C.③④⑤
D.③⑤⑥
10.如图,在中,,分别平分和,则( )
A.
B.
C.
D.
二、填空题(每小题3分,共24分).
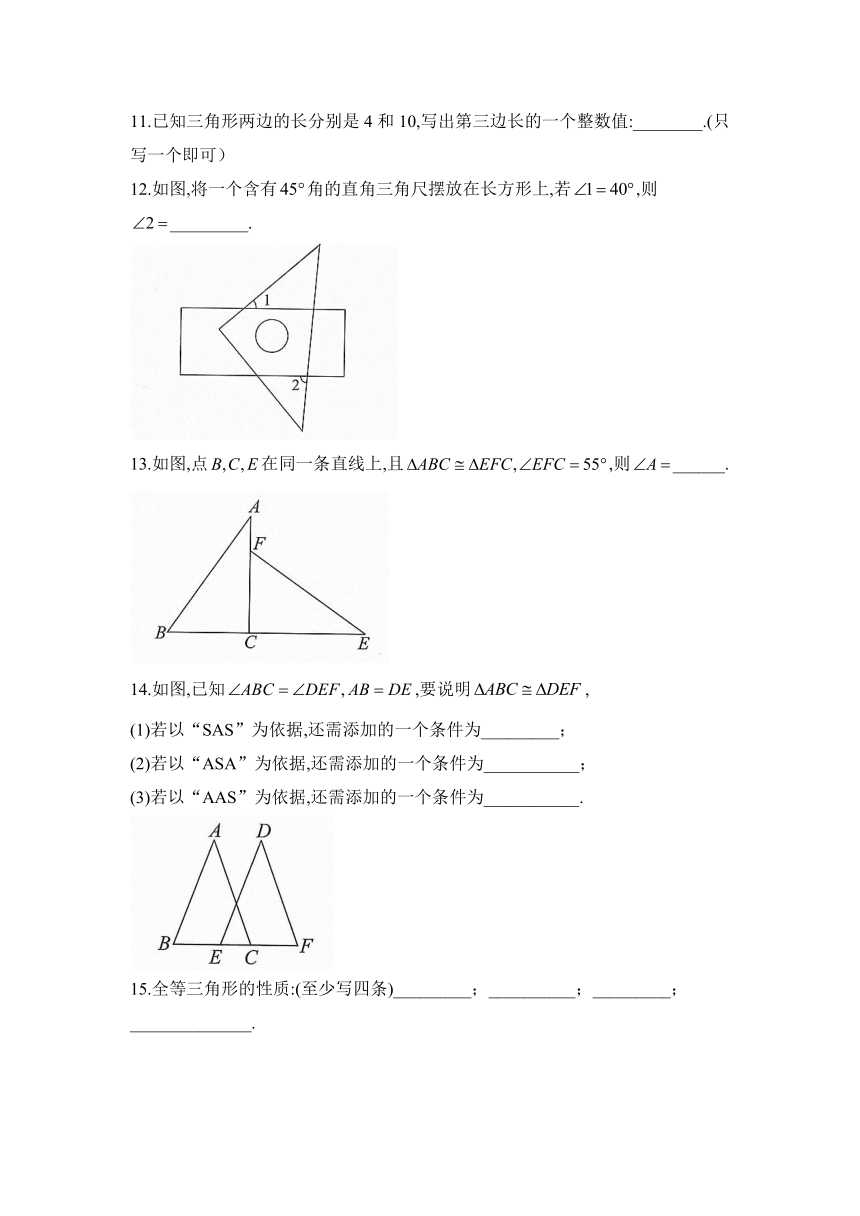
11.已知三角形两边的长分别是4和10,写出第三边长的一个整数值:________.(只写一个即可)
12.如图,将一个含有角的直角三角尺摆放在长方形上,若,则_________.
13.如图,点在同一条直线上,且,则______.
14.如图,已知,要说明,
(1)若以“SAS”为依据,还需添加的一个条件为_________;
(2)若以“ASA”为依据,还需添加的一个条件为___________;
(3)若以“AAS”为依据,还需添加的一个条件为___________.
15.全等三角形的性质:(至少写四条)_________;__________;_________;______________.
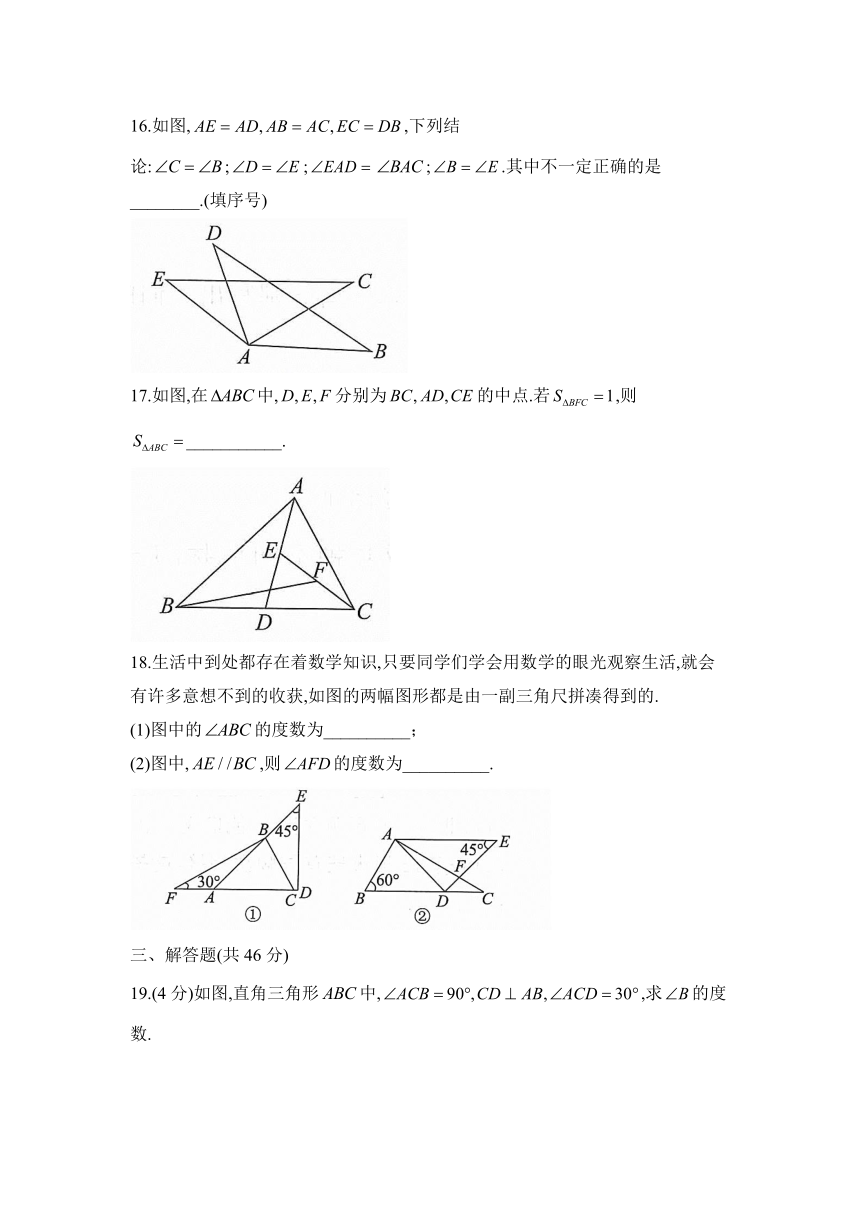
16.如图,,下列结论:;;;.其中不一定正确的是________.(填序号)
17.如图,在中,分别为的中点.若,则___________.
18.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图的两幅图形都是由一副三角尺拼凑得到的.
(1)图中的的度数为__________;
(2)图中,,则的度数为__________.
三、解答题(共46分)
19.(4分)如图,直角三角形中,,求的度数.
20.(8分)如图,在和中,点在同一条直线上,且,试说明:.
21.(8分)课堂活动上,小英用木棒在桌面上拼摆三角形,分别用3根、5根、6根火柴首尾顺次相接,能搭成一个不同形状的三角形.
(1)4根火柴首尾顺次相接,能搭成一个三角形吗
(2)8根、12根火柴首尾顺次相接,能搭成几种不同形状的三角形 请分别写出它们的边长.
22.(8分)如图,点在同一条直线上,,试说明:.
23.(8分)(2020-无锡)如图,已知.
试说明:(1);
(2).
24.(10分)以点为顶点作两个等腰直角三角形(,如图所示放置,使得一直角边重合,连接.
(1)试说明:;
(2)延长交于点,求的度数;
(3)若如图放置,上面的结论还成立旳 请简单说明理由.
参考答案
1.答案:B
2.答案:D
3.答案:D
4.答案:D
5.答案:C
6.答案:C
7.答案:C
8.答案:B
9.答案:B
10.答案:D
11.答案:9(答案不唯一)
12.答案:85°
13.答案:35°
14.答案:(1)BC=EF(或BE=CF)
(2)∠A=∠D
(3)∠ACB=∠F
15.答案:全等三角形的对应边相等
全等三角形的对应角相等
全等三角形的周长相等
全等三角形的面积相等(答案不唯一)
16.答案:④
17.答案:4
18.答案:(1)75°(2)75°
19.答案:见解析
解析:因为∠ACB=90°,∠ACD=30°,
所以∠BCD=∠ACB-∠ACD=90°-30°=60°.
因为CD⊥AB,所以∠CDB=90°,所以∠B=90°-∠BCD=90°-60°=30°.
20.答案:见解析
解析:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
所以△ABC≌△DEF(SSS),所以∠ABC=∠DEF.
21.答案:见解析
解析:(1)4根火柴不能搭成一个三角形.
(2)8根火柴能搭成一种三角形,其三边长分别为3,3,2;
12根火柴能搭成3种不同形状的三角形,其三边长分别是4,4,4或5,5,2或3,4,5.
22.答案:见解析
解析:因为BF=DE,
所以BF+EF=DE+EF,
即BE=DF.
在△ABE和△CDF中,
所以△ABE≌△CDF(SAS),
所以∠AEB=∠CFD,
所以AE∥CF.
23.答案:见解析
解析:(1)因为BE=CF,所以BE-EF=CF-EF,即BF=CE.
因为AB∥CD,所以∠B=∠C.
在△ABF和△DCE中,
以△ABF≌△DCE(SAS).
(2)因为△ABF≌△DCE,
所以∠AFB=∠DEC,所以∠AFE=∠DEF,所以AF∥DE.
24.答案:见解析
解析:(1)在△ADB和△AEC中,
所以△ADB≌△AEC(SAS),
所以BD=CE.
(2)由(1)知△ADB≌△AEC,
所以∠DBA=∠ECA,
所以∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°.
(3)BD=CE且∠BFC=90°同样成立.理由如下:
因为△ABC,△ADE是等腰直角三角形,
所以AB=AC,AD=AE,∠BAC=∠DAE=90°,
所以∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠CAE,
所以△ADB≌△AEC,
所以BD=CE,∠ABF=∠ACF.
设BD交AC于点M,因为∠AMB=∠CMF.
所以∠BFC=∠BAC=90°.
一、选择题
1.长度分别为的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4
B.5
C.6
D.7
2.在中,若,则是( )
A.等边三角形
B.锐角三角形
C.直角三角形
D.钝角三角形
3.下列说法中正确的是( )
A.面积相等的两个图形是全等图形
B.周长相等的两个图形是全等图形
C.所有正方形都是全等图形
D.能够完全重合的两个图形是全等图形
4.有四根长度分别为(为正整数)的木棒,从中任取三根,首尾顺次相接,都能组成一个三角形,则组成的三角形的周长( )
A.最小值是11
B.最小值是12
C.最大值是14
D.最大值是15
5.已知是的三边长,且,那么( )
A.
B.
C.
D.不能确定
6.如图,工人师傅做了一个长方形窗框,分别是四条边的中点,为了稳固,需要在窗框上钉一根木条,这根木条的两端不应钉在( )
A.两点处
B.两点处
C.两点处
D.两点处
7.如图,已知,下列结论中正确的个数是( )
;;;;;;
.
A.4
B.5
C.6
D.7
8.如图,,则不一定能使的条件是( )
A.
B.
C.
D.
9.在和中,已知条件:;;;
;;.下列各组条件中不能判定的是( )
A.①②③
B.②③④
C.③④⑤
D.③⑤⑥
10.如图,在中,,分别平分和,则( )
A.
B.
C.
D.
二、填空题(每小题3分,共24分).
11.已知三角形两边的长分别是4和10,写出第三边长的一个整数值:________.(只写一个即可)
12.如图,将一个含有角的直角三角尺摆放在长方形上,若,则_________.
13.如图,点在同一条直线上,且,则______.
14.如图,已知,要说明,
(1)若以“SAS”为依据,还需添加的一个条件为_________;
(2)若以“ASA”为依据,还需添加的一个条件为___________;
(3)若以“AAS”为依据,还需添加的一个条件为___________.
15.全等三角形的性质:(至少写四条)_________;__________;_________;______________.
16.如图,,下列结论:;;;.其中不一定正确的是________.(填序号)
17.如图,在中,分别为的中点.若,则___________.
18.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图的两幅图形都是由一副三角尺拼凑得到的.
(1)图中的的度数为__________;
(2)图中,,则的度数为__________.
三、解答题(共46分)
19.(4分)如图,直角三角形中,,求的度数.
20.(8分)如图,在和中,点在同一条直线上,且,试说明:.
21.(8分)课堂活动上,小英用木棒在桌面上拼摆三角形,分别用3根、5根、6根火柴首尾顺次相接,能搭成一个不同形状的三角形.
(1)4根火柴首尾顺次相接,能搭成一个三角形吗
(2)8根、12根火柴首尾顺次相接,能搭成几种不同形状的三角形 请分别写出它们的边长.
22.(8分)如图,点在同一条直线上,,试说明:.
23.(8分)(2020-无锡)如图,已知.
试说明:(1);
(2).
24.(10分)以点为顶点作两个等腰直角三角形(,如图所示放置,使得一直角边重合,连接.
(1)试说明:;
(2)延长交于点,求的度数;
(3)若如图放置,上面的结论还成立旳 请简单说明理由.
参考答案
1.答案:B
2.答案:D
3.答案:D
4.答案:D
5.答案:C
6.答案:C
7.答案:C
8.答案:B
9.答案:B
10.答案:D
11.答案:9(答案不唯一)
12.答案:85°
13.答案:35°
14.答案:(1)BC=EF(或BE=CF)
(2)∠A=∠D
(3)∠ACB=∠F
15.答案:全等三角形的对应边相等
全等三角形的对应角相等
全等三角形的周长相等
全等三角形的面积相等(答案不唯一)
16.答案:④
17.答案:4
18.答案:(1)75°(2)75°
19.答案:见解析
解析:因为∠ACB=90°,∠ACD=30°,
所以∠BCD=∠ACB-∠ACD=90°-30°=60°.
因为CD⊥AB,所以∠CDB=90°,所以∠B=90°-∠BCD=90°-60°=30°.
20.答案:见解析
解析:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
所以△ABC≌△DEF(SSS),所以∠ABC=∠DEF.
21.答案:见解析
解析:(1)4根火柴不能搭成一个三角形.
(2)8根火柴能搭成一种三角形,其三边长分别为3,3,2;
12根火柴能搭成3种不同形状的三角形,其三边长分别是4,4,4或5,5,2或3,4,5.
22.答案:见解析
解析:因为BF=DE,
所以BF+EF=DE+EF,
即BE=DF.
在△ABE和△CDF中,
所以△ABE≌△CDF(SAS),
所以∠AEB=∠CFD,
所以AE∥CF.
23.答案:见解析
解析:(1)因为BE=CF,所以BE-EF=CF-EF,即BF=CE.
因为AB∥CD,所以∠B=∠C.
在△ABF和△DCE中,
以△ABF≌△DCE(SAS).
(2)因为△ABF≌△DCE,
所以∠AFB=∠DEC,所以∠AFE=∠DEF,所以AF∥DE.
24.答案:见解析
解析:(1)在△ADB和△AEC中,
所以△ADB≌△AEC(SAS),
所以BD=CE.
(2)由(1)知△ADB≌△AEC,
所以∠DBA=∠ECA,
所以∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°.
(3)BD=CE且∠BFC=90°同样成立.理由如下:
因为△ABC,△ADE是等腰直角三角形,
所以AB=AC,AD=AE,∠BAC=∠DAE=90°,
所以∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠CAE,
所以△ADB≌△AEC,
所以BD=CE,∠ABF=∠ACF.
设BD交AC于点M,因为∠AMB=∠CMF.
所以∠BFC=∠BAC=90°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
