湘教版数学七年级下册 第4章 相交线与平行线 单元检测(word版含答案)
文档属性
| 名称 | 湘教版数学七年级下册 第4章 相交线与平行线 单元检测(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览

文档简介
第4章 相交线与平行线
学校:___________姓名:___________班级:___________考号:___________
一、选择题
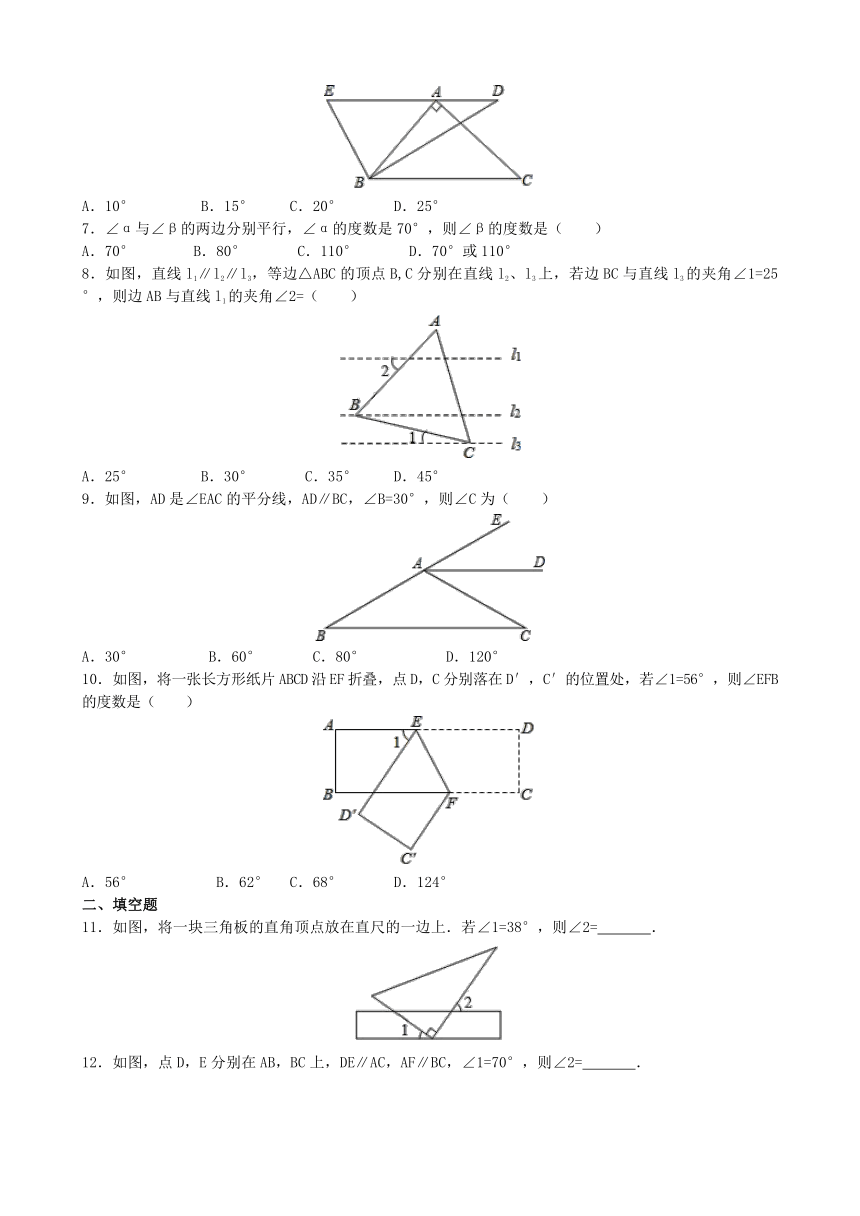
1.如图,直线a,b被直线c所截,且a∥b,下列结论不正确的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠2=∠3
2.如图,已知AC∥DE,∠B=24°,∠D=58°,则∠C=( )
A.24° B.34° C.58° D.82°
3.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,若∠1=25°,则∠2的度数是( )
A.35° B.30° C.25° D.20°
4.如图,已知AB∥CD,∠EBA=45°,那么∠E+∠D的度数为( )
A.30° B.45° C.60° D.90°
5.如图,AB∥CD,EF⊥AB于E,若∠1=60°,则∠2的度数是( )
A.35° B.30° C.25° D.20°
6.将一副三角板如图放置,使点A在DE上,BC∥DE,∠C=45°,∠D=30°,则∠ABD的度数为( )
A.10° B.15° C.20° D.25°
7.∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )
A.70° B.80° C.110° D.70°或110°
8.如图,直线l1∥l2∥l3,等边△ABC的顶点B,C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=( )
A.25° B.30° C.35° D.45°
9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
10.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在D′,C′的位置处,若∠1=56°,则∠EFB的度数是( )
A.56° B.62° C.68° D.124°
二、填空题
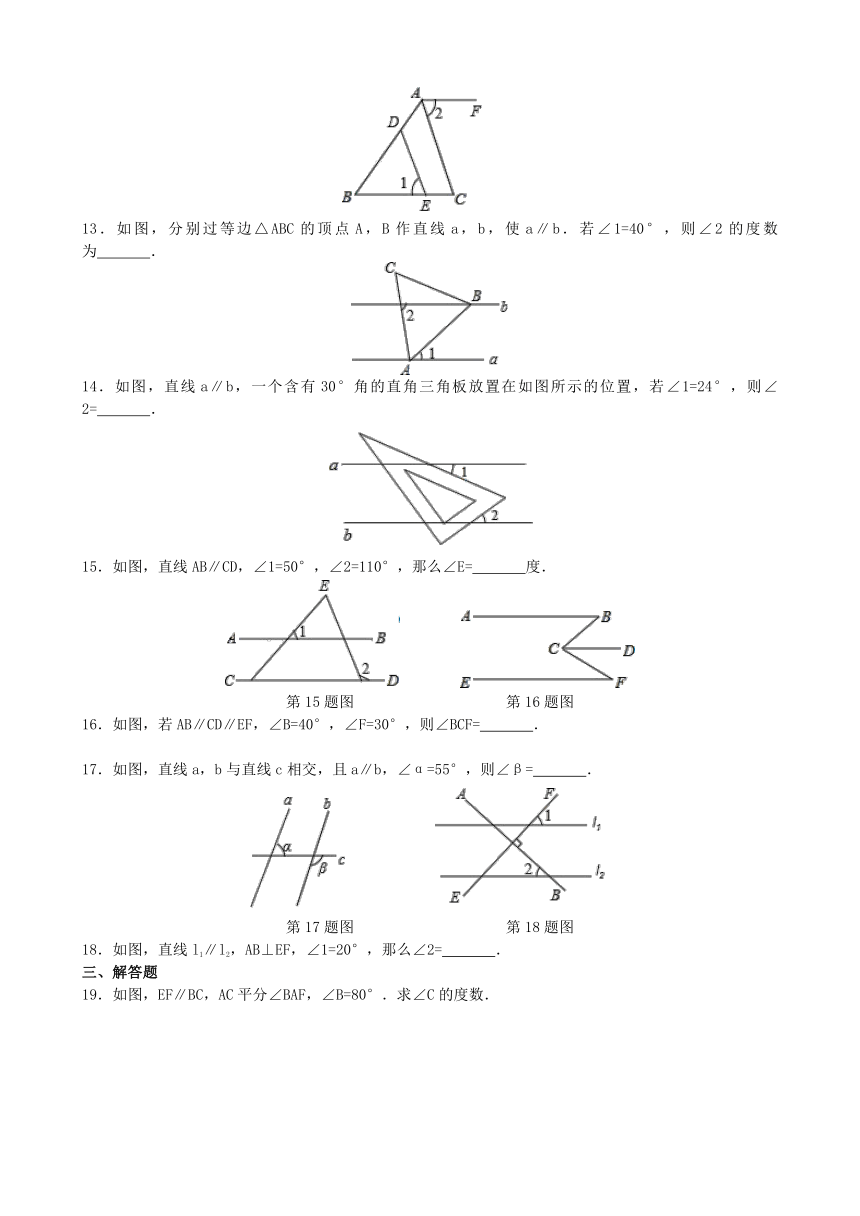
11.如图,将一块三角板的直角顶点放在直尺的一边上.若∠1=38°,则∠2= .
12.如图,点D,E分别在AB,BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= .
13.如图,分别过等边△ABC的顶点A,B作直线a,b,使a∥b.若∠1=40°,则∠2的度数为 .
14.如图,直线a∥b,一个含有30°角的直角三角板放置在如图所示的位置,若∠1=24°,则∠2= .
15.如图,直线AB∥CD,∠1=50°,∠2=110°,那么∠E= 度.
第15题图 第16题图
16.如图,若AB∥CD∥EF,∠B=40°,∠F=30°,则∠BCF= .
17.如图,直线a,b与直线c相交,且a∥b,∠α=55°,则∠β= .
第17题图 第18题图
18.如图,直线l1∥l2,AB⊥EF,∠1=20°,那么∠2= .
三、解答题
19.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
20.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
21.如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线( ),
∴∠ABD=∠DBC( ).
∵ED∥BC( ),
∴∠BDE=∠DBC( ).
∴ ( ).
又∵∠FED=∠BDE( ),
∴ ∥ ( ).
∴∠AEF=∠ABD( ).
∴∠AEF=∠DEF( ).
∴EF是∠AED的平分线( ).
22.如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
23.如图,已知平面内有两条直线AB,CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论;
(2)当点P移动到图2、图3的位置时,∠P、∠A、∠C又有怎样的关系?请分别写出你的结论.
图1 图2 图3
24.如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
参考答案
一、选择题
1.D 2.B 3.D 4.B 5.B 6.B 7.D 8.C 9.A 10.B
二、填空题
11.52° 12.70° 13.80° 14.36° 15.60
16.70° 17.125° 18.70°
三、解答题
19.解:∵EF∥BC,∴∠BAF=180°﹣∠B=100°.
∵AC平分∠BAF,∴∠CAF=∠BAF=50°.
∵EF∥BC,∴∠C=∠CAF=50°.
20.解:∵AB⊥BC,∴∠ABC=90°,
∴∠1+∠3=90°.
∵∠1=55°,∴∠3=35°.
∵a∥b,∴∠2=∠3=35°.
21.解:证明:∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线定义).
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等).
∴∠ABD=∠BDE(等量代换).
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行).
∴∠AEF=∠ABD(两直线平行,同位角相等).
∴∠AEF=∠DEF(等量代换).
∴EF是∠AED的平分线(角平分线定义).
22.解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD,CE即为所求;
(3)4
23.解:(1)∠APC=∠A+∠C.
证明:如图1,过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C.
(2)如图2,∠APC+∠A+∠C=360°,
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∴∠APC+∠A+∠C=360°;
如图3,∠APC=∠C﹣∠A.
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠C=∠CPE,∠A=∠APE,
∴∠APC=∠CPE﹣∠APE=∠C﹣∠A.
图1 图2 图3
24.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°.
∵∠A=60°,∴∠ABN=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠NBP,
∴∠CBD=∠ABN=60°;
(2)不变化,∠APB=2∠ADB.
证明:∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN.
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN.
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=(120°﹣60°)=30°,
故答案为:30°.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,直线a,b被直线c所截,且a∥b,下列结论不正确的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠2=∠3
2.如图,已知AC∥DE,∠B=24°,∠D=58°,则∠C=( )
A.24° B.34° C.58° D.82°
3.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,若∠1=25°,则∠2的度数是( )
A.35° B.30° C.25° D.20°
4.如图,已知AB∥CD,∠EBA=45°,那么∠E+∠D的度数为( )
A.30° B.45° C.60° D.90°
5.如图,AB∥CD,EF⊥AB于E,若∠1=60°,则∠2的度数是( )
A.35° B.30° C.25° D.20°
6.将一副三角板如图放置,使点A在DE上,BC∥DE,∠C=45°,∠D=30°,则∠ABD的度数为( )
A.10° B.15° C.20° D.25°
7.∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )
A.70° B.80° C.110° D.70°或110°
8.如图,直线l1∥l2∥l3,等边△ABC的顶点B,C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=( )
A.25° B.30° C.35° D.45°
9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
10.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在D′,C′的位置处,若∠1=56°,则∠EFB的度数是( )
A.56° B.62° C.68° D.124°
二、填空题
11.如图,将一块三角板的直角顶点放在直尺的一边上.若∠1=38°,则∠2= .
12.如图,点D,E分别在AB,BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= .
13.如图,分别过等边△ABC的顶点A,B作直线a,b,使a∥b.若∠1=40°,则∠2的度数为 .
14.如图,直线a∥b,一个含有30°角的直角三角板放置在如图所示的位置,若∠1=24°,则∠2= .
15.如图,直线AB∥CD,∠1=50°,∠2=110°,那么∠E= 度.
第15题图 第16题图
16.如图,若AB∥CD∥EF,∠B=40°,∠F=30°,则∠BCF= .
17.如图,直线a,b与直线c相交,且a∥b,∠α=55°,则∠β= .
第17题图 第18题图
18.如图,直线l1∥l2,AB⊥EF,∠1=20°,那么∠2= .
三、解答题
19.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
20.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
21.如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线( ),
∴∠ABD=∠DBC( ).
∵ED∥BC( ),
∴∠BDE=∠DBC( ).
∴ ( ).
又∵∠FED=∠BDE( ),
∴ ∥ ( ).
∴∠AEF=∠ABD( ).
∴∠AEF=∠DEF( ).
∴EF是∠AED的平分线( ).
22.如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
23.如图,已知平面内有两条直线AB,CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论;
(2)当点P移动到图2、图3的位置时,∠P、∠A、∠C又有怎样的关系?请分别写出你的结论.
图1 图2 图3
24.如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
参考答案
一、选择题
1.D 2.B 3.D 4.B 5.B 6.B 7.D 8.C 9.A 10.B
二、填空题
11.52° 12.70° 13.80° 14.36° 15.60
16.70° 17.125° 18.70°
三、解答题
19.解:∵EF∥BC,∴∠BAF=180°﹣∠B=100°.
∵AC平分∠BAF,∴∠CAF=∠BAF=50°.
∵EF∥BC,∴∠C=∠CAF=50°.
20.解:∵AB⊥BC,∴∠ABC=90°,
∴∠1+∠3=90°.
∵∠1=55°,∴∠3=35°.
∵a∥b,∴∠2=∠3=35°.
21.解:证明:∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线定义).
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等).
∴∠ABD=∠BDE(等量代换).
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行).
∴∠AEF=∠ABD(两直线平行,同位角相等).
∴∠AEF=∠DEF(等量代换).
∴EF是∠AED的平分线(角平分线定义).
22.解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD,CE即为所求;
(3)4
23.解:(1)∠APC=∠A+∠C.
证明:如图1,过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C.
(2)如图2,∠APC+∠A+∠C=360°,
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∴∠APC+∠A+∠C=360°;
如图3,∠APC=∠C﹣∠A.
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠C=∠CPE,∠A=∠APE,
∴∠APC=∠CPE﹣∠APE=∠C﹣∠A.
图1 图2 图3
24.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°.
∵∠A=60°,∴∠ABN=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠NBP,
∴∠CBD=∠ABN=60°;
(2)不变化,∠APB=2∠ADB.
证明:∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN.
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN.
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=(120°﹣60°)=30°,
故答案为:30°.
