第一章 三角形的证明单元测试题(含答案)
文档属性
| 名称 | 第一章 三角形的证明单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 702.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 15:55:40 | ||
图片预览


文档简介
《第一章 三角形的证明》章末复习
一、选择题
1.若要运用反证法证明“若,则”,首先应该假设( )
A.
B.
C.
D.
2.如图,是等边底边上的中线,的垂直平分线交于点,交于点,若,则的长为( )
A.1
B.
C.
D.2
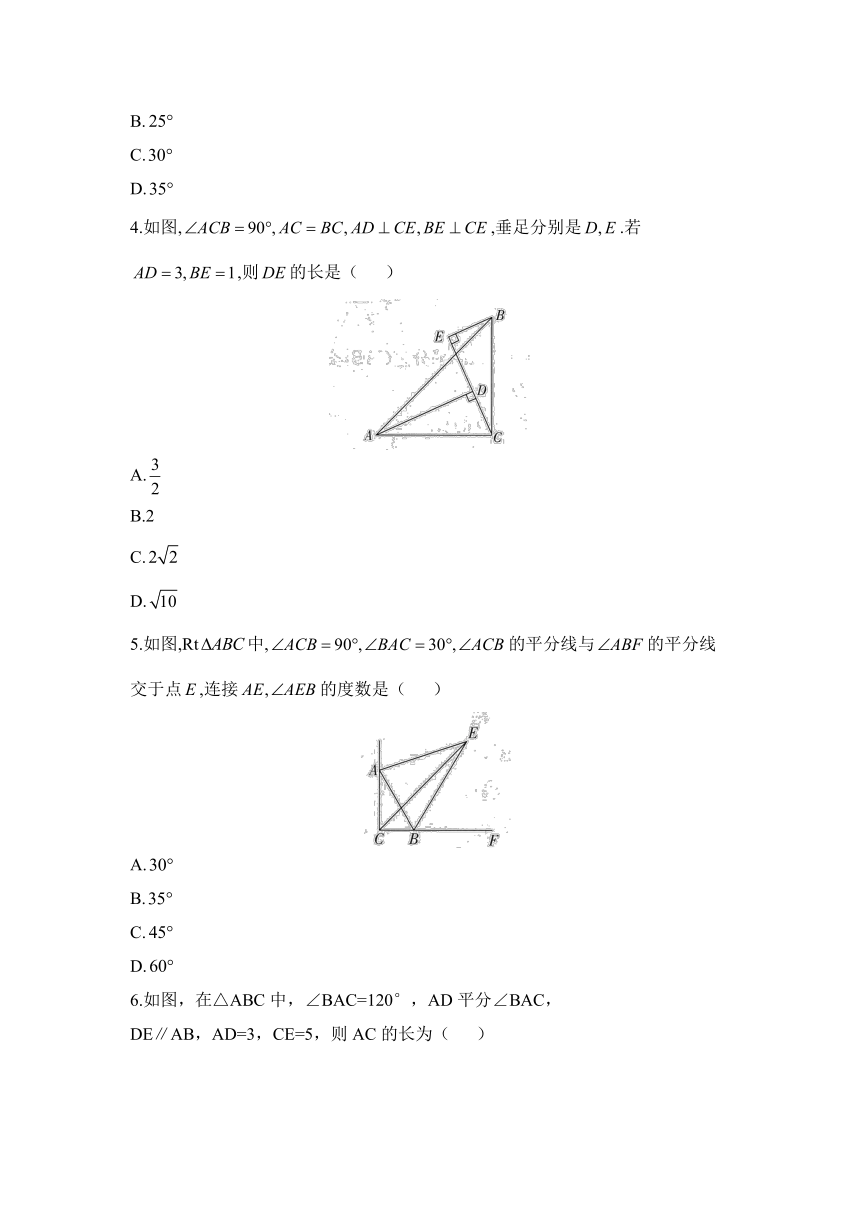
3.如图,在中,是边上的高线,点在上,且,则的度数为( )
A.
B.
C.
D.
4.如图,,垂足分别是.若,则的长是( )
A.
B.2
C.
D.
5.如图,Rt中,的平分线与的平分线交于点,连接的度数是( )
A.
B.
C.
D.
6.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,
DE∥AB,AD=3,CE=5,则AC的长为( )
A.9
B.8
C.6
D.7
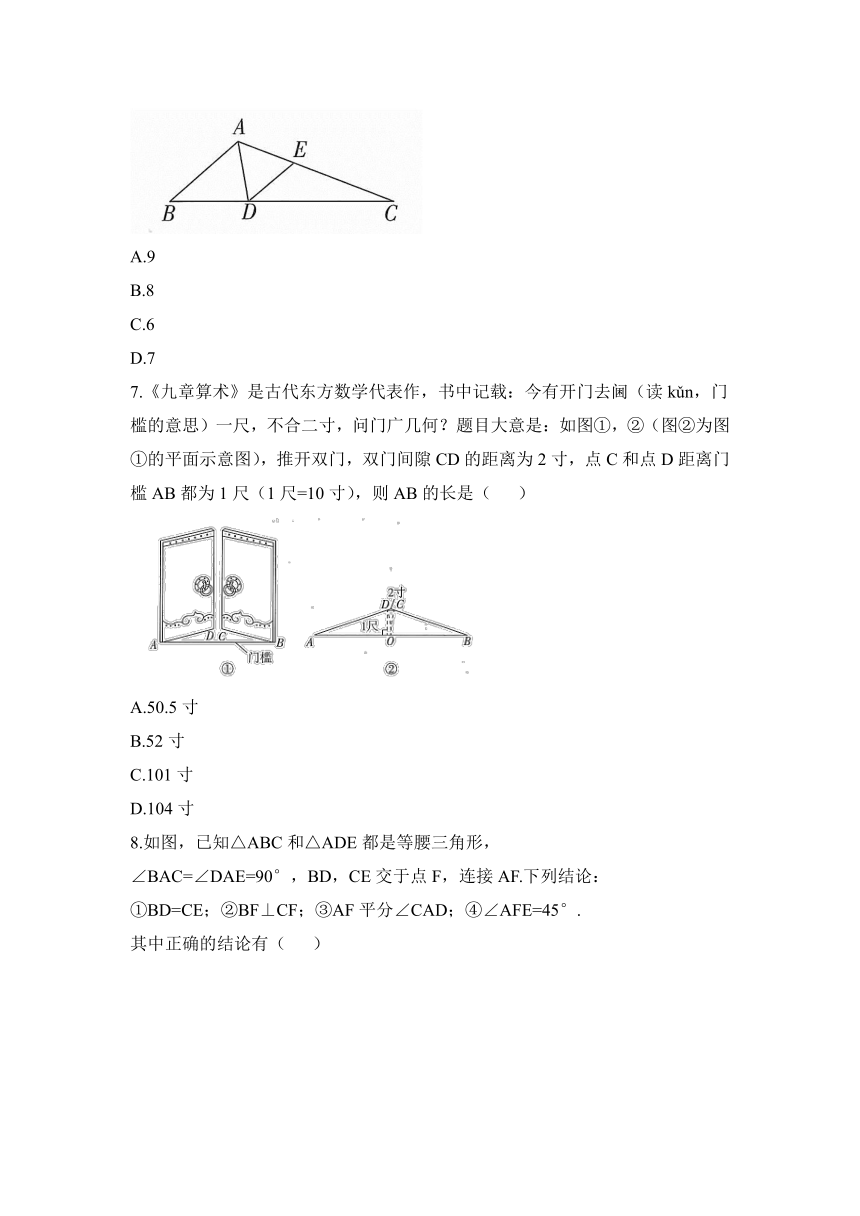
7.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①,②(图②为图①的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸
B.52寸
C.101寸
D.104寸
8.如图,已知△ABC和△ADE都是等腰三角形,
∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:
①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
9.命题“对顶角相等”的逆命题是___________.
10.等边△ABC的周长为9,则△ABC的面积为_________.
11.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F,若∠F=30°,DE=1,则BE的长是_______.
12.如图,P是△ABC的三条内角平分线的交点,连接PA,PB,PC,
设△PAB,△PBC,△PAC的面积分别为,则____(填“>”“<”或“=”)
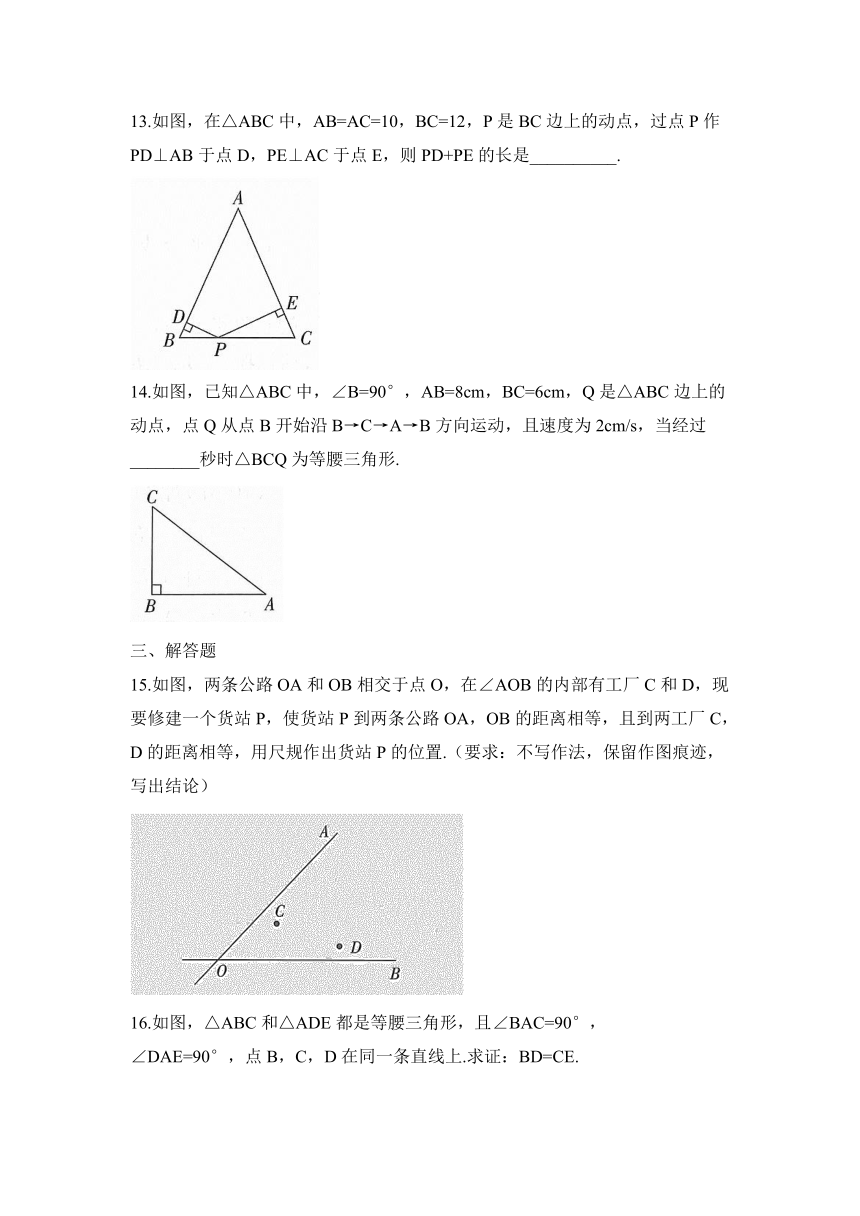
13.如图,在△ABC中,AB=AC=10,BC=12,P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是__________.
14.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,Q是△ABC边上的动点,点Q从点B开始沿B→C→A→B方向运动,且速度为2cm/s,当经过________秒时△BCQ为等腰三角形.
三、解答题
15.如图,两条公路OA和OB相交于点O,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA,OB的距离相等,且到两工厂C,D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
16.如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,
∠DAE=90°,点B,C,D在同一条直线上.求证:BD=CE.
17.如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,垂足分别为C,D,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线;
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
18.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.下面我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
________.(填“是”或“不是”)
(2)若某三角形的三边长分别为1,,2,则该三角形是不是奇异三角形?请做出判断并写出判断依据.
(3)在Rt△ABC中,两边长分别为a,c,且,则这个三角形是不是奇异三角形?请做出判断并写出判断依据.
探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,
若Rt△ABC是奇异三角形,求.
19.【发现】如图①,△ABD,△AEC都是等边三角形.易知:BE______CD,且BE与CD的夹角∠BOD=_______°.
【探究】如图②,△ABD,△AEC都是等腰直角三角形,
∠DAB=∠EAC=90°,BE,CD交于点O,判断BE与CD的关系,并说明理由.
【拓展】如图③,在平面直角坐标系中,AP=OP,点A的坐标为(0,1),点B为y轴正半轴上的一动点,点C为第一象限的一点,且BP=CP,
∠BPC=∠OPA=45°,CA的延长线交x轴于点E,当点B运动时,点E的坐标是否也随着变化?若不变,求出点E的坐标;若变化,说明理由.
参考答案
1.答案:D
2.答案:C
3.答案:B
4.答案:B
5.答案:C
6.答案:B
7.答案:C
8.答案:C
9.答案:相等的角为对顶角
10.答案:
11.答案:2
12.答案:<
13.答案:
14.答案:5.5或6或6.6或9
15.答案:见解析
解析:如答图,CD的垂直平分线与∠AOB的平分线的交点即为所求点P.
16.答案:见解析
解析:证明:∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AD=AE.
又∵∠EAC=∠EAD+∠CAD,∠DAB=∠BAC+∠CAD,
∠EAD=∠BAC=90°,
∴∠DAB=∠EAC.
在△ADB和△AEC中,
∴△ADB≌△AEC(SAS),∴BD=CE.
17.答案:见解析
解析:(1)证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE又∵OE=OE,∴Rt△ODE≌Rt△OCE,
∴OD=OC,∴OE是CD的垂直平分线.
(2)解:OE=4EF.证明如下:
∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°.
由(1)得OD=OC,
∴∠ODC=∠OCD=60°.
∵ED⊥OA,∴OE=2DE,∠EDF=30°,
∵OE是CD的垂直平分线,∴∠EFD=90°,
∴DE=2EF,∴OE=4EF.
18.答案:见解析
解析:(1)是
(2)解:该三角形是奇异三角形.
∵,
∴该三角形是奇异三角形.
(3)解:当为斜边时,,不是奇异三角形;
当为斜边时,,
∵,
∴,
∴是奇异三角形.
探究:在Rt中,,
∴
∵
∵是奇异三角形,∴,
∴
∴.
19.答案:见解析
解析:【发现】= 60
解析:∵△ABD,△AEC都是等边三角形,
∴AD=AB,AC=AE,∠BAD=60°,∠CAE=60°,
∴∠BAD=∠CAE,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴DC=BE,∠ADC=∠ABE.
∵∠ADB+∠ABD=120°,
∴∠ODB+∠ABD+∠ABE=120°,
即∠ODB+∠OBD=120°,
∴∠BOD=180°-(∠ODB+∠OBD)=60°.
【探究】BE=CD,BE⊥CD.
理由如下:∵△ABD,△AEC都是等腰直角三角形,
∴AD=AB,AC=AE,又∠DAB=∠EAC=90°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
∴∠DAC=∠BAE.
在△DAC和△BAE中,,
∴△DAC≌△BAE(SAS),
∴DC=BE,∠ADC=∠ABE.
∵∠ADB+∠ABD=90°,
∴∠ADO+∠ADB+∠OBD=90°,
即∠ODB+∠OBD=90°,
∴∠BOD=90°,
∴BE⊥CD,∴BE=CD,BE⊥CD.
【拓展】点E的坐标不变
∵AP=OP,∠OPA=45°,
∴∠PAO=∠POA=×(180°-45°)=67.5°,
同(1)的方法可得,△CAP≌△BOP,
∴∠CAP=∠BOP=67.5°,
∴∠CAB=180°-∠CAP-∠PAO=45°,
∴∠OAE=∠CAB=45°,∴OE=OA=1,
∴点E的坐标为(-1,0).
一、选择题
1.若要运用反证法证明“若,则”,首先应该假设( )
A.
B.
C.
D.
2.如图,是等边底边上的中线,的垂直平分线交于点,交于点,若,则的长为( )
A.1
B.
C.
D.2
3.如图,在中,是边上的高线,点在上,且,则的度数为( )
A.
B.
C.
D.
4.如图,,垂足分别是.若,则的长是( )
A.
B.2
C.
D.
5.如图,Rt中,的平分线与的平分线交于点,连接的度数是( )
A.
B.
C.
D.
6.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,
DE∥AB,AD=3,CE=5,则AC的长为( )
A.9
B.8
C.6
D.7
7.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①,②(图②为图①的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸
B.52寸
C.101寸
D.104寸
8.如图,已知△ABC和△ADE都是等腰三角形,
∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:
①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
9.命题“对顶角相等”的逆命题是___________.
10.等边△ABC的周长为9,则△ABC的面积为_________.
11.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F,若∠F=30°,DE=1,则BE的长是_______.
12.如图,P是△ABC的三条内角平分线的交点,连接PA,PB,PC,
设△PAB,△PBC,△PAC的面积分别为,则____(填“>”“<”或“=”)
13.如图,在△ABC中,AB=AC=10,BC=12,P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是__________.
14.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,Q是△ABC边上的动点,点Q从点B开始沿B→C→A→B方向运动,且速度为2cm/s,当经过________秒时△BCQ为等腰三角形.
三、解答题
15.如图,两条公路OA和OB相交于点O,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA,OB的距离相等,且到两工厂C,D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
16.如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,
∠DAE=90°,点B,C,D在同一条直线上.求证:BD=CE.
17.如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,垂足分别为C,D,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线;
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
18.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.下面我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
________.(填“是”或“不是”)
(2)若某三角形的三边长分别为1,,2,则该三角形是不是奇异三角形?请做出判断并写出判断依据.
(3)在Rt△ABC中,两边长分别为a,c,且,则这个三角形是不是奇异三角形?请做出判断并写出判断依据.
探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,
若Rt△ABC是奇异三角形,求.
19.【发现】如图①,△ABD,△AEC都是等边三角形.易知:BE______CD,且BE与CD的夹角∠BOD=_______°.
【探究】如图②,△ABD,△AEC都是等腰直角三角形,
∠DAB=∠EAC=90°,BE,CD交于点O,判断BE与CD的关系,并说明理由.
【拓展】如图③,在平面直角坐标系中,AP=OP,点A的坐标为(0,1),点B为y轴正半轴上的一动点,点C为第一象限的一点,且BP=CP,
∠BPC=∠OPA=45°,CA的延长线交x轴于点E,当点B运动时,点E的坐标是否也随着变化?若不变,求出点E的坐标;若变化,说明理由.
参考答案
1.答案:D
2.答案:C
3.答案:B
4.答案:B
5.答案:C
6.答案:B
7.答案:C
8.答案:C
9.答案:相等的角为对顶角
10.答案:
11.答案:2
12.答案:<
13.答案:
14.答案:5.5或6或6.6或9
15.答案:见解析
解析:如答图,CD的垂直平分线与∠AOB的平分线的交点即为所求点P.
16.答案:见解析
解析:证明:∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AD=AE.
又∵∠EAC=∠EAD+∠CAD,∠DAB=∠BAC+∠CAD,
∠EAD=∠BAC=90°,
∴∠DAB=∠EAC.
在△ADB和△AEC中,
∴△ADB≌△AEC(SAS),∴BD=CE.
17.答案:见解析
解析:(1)证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE又∵OE=OE,∴Rt△ODE≌Rt△OCE,
∴OD=OC,∴OE是CD的垂直平分线.
(2)解:OE=4EF.证明如下:
∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°.
由(1)得OD=OC,
∴∠ODC=∠OCD=60°.
∵ED⊥OA,∴OE=2DE,∠EDF=30°,
∵OE是CD的垂直平分线,∴∠EFD=90°,
∴DE=2EF,∴OE=4EF.
18.答案:见解析
解析:(1)是
(2)解:该三角形是奇异三角形.
∵,
∴该三角形是奇异三角形.
(3)解:当为斜边时,,不是奇异三角形;
当为斜边时,,
∵,
∴,
∴是奇异三角形.
探究:在Rt中,,
∴
∵
∵是奇异三角形,∴,
∴
∴.
19.答案:见解析
解析:【发现】= 60
解析:∵△ABD,△AEC都是等边三角形,
∴AD=AB,AC=AE,∠BAD=60°,∠CAE=60°,
∴∠BAD=∠CAE,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴DC=BE,∠ADC=∠ABE.
∵∠ADB+∠ABD=120°,
∴∠ODB+∠ABD+∠ABE=120°,
即∠ODB+∠OBD=120°,
∴∠BOD=180°-(∠ODB+∠OBD)=60°.
【探究】BE=CD,BE⊥CD.
理由如下:∵△ABD,△AEC都是等腰直角三角形,
∴AD=AB,AC=AE,又∠DAB=∠EAC=90°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
∴∠DAC=∠BAE.
在△DAC和△BAE中,,
∴△DAC≌△BAE(SAS),
∴DC=BE,∠ADC=∠ABE.
∵∠ADB+∠ABD=90°,
∴∠ADO+∠ADB+∠OBD=90°,
即∠ODB+∠OBD=90°,
∴∠BOD=90°,
∴BE⊥CD,∴BE=CD,BE⊥CD.
【拓展】点E的坐标不变
∵AP=OP,∠OPA=45°,
∴∠PAO=∠POA=×(180°-45°)=67.5°,
同(1)的方法可得,△CAP≌△BOP,
∴∠CAP=∠BOP=67.5°,
∴∠CAB=180°-∠CAP-∠PAO=45°,
∴∠OAE=∠CAB=45°,∴OE=OA=1,
∴点E的坐标为(-1,0).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
