北师大版八年级数学下册《第六章 平行四边形》单元检测(含答案)
文档属性
| 名称 | 北师大版八年级数学下册《第六章 平行四边形》单元检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览


文档简介
《第六章 平行四边形》章末复习
一、选择题
1.若一个正多边形的一个外角是,则该正多边形的内角和为( )
A.
B.
C.
D.
2.如图,将一副三角板在平行四边形中作如下摆放,,那么的度数为( )
A.
B.
C.
D.
3.如图,的周长为52,对角线相交于点,点是CD的中点,BD=18,则△DOE的周长是( )
A.22
B.26
C.31
D.35
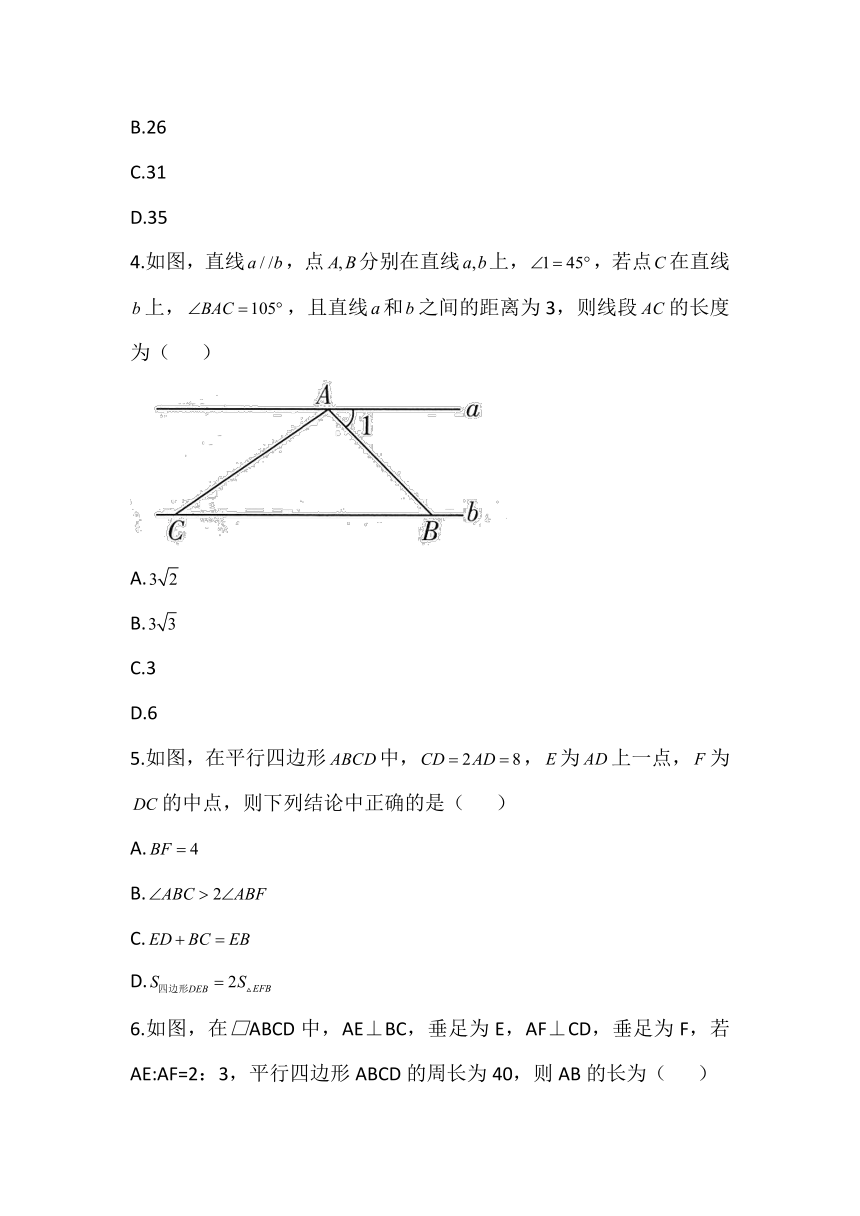
4.如图,直线,点分别在直线上,,若点在直线上,,且直线和之间的距离为3,则线段的长度为( )
A.
B.
C.3
D.6
5.如图,在平行四边形中,,为上一点,为的中点,则下列结论中正确的是( )
A.
B.
C.
D.
6.如图,在□ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2:3,平行四边形ABCD的周长为40,则AB的长为( )
A.12
B.9
C.8
D.6
7.如图,在中,,的平分线交于点,交的延长线于点,则的长为( )
A.4
B.2
C.3
D.
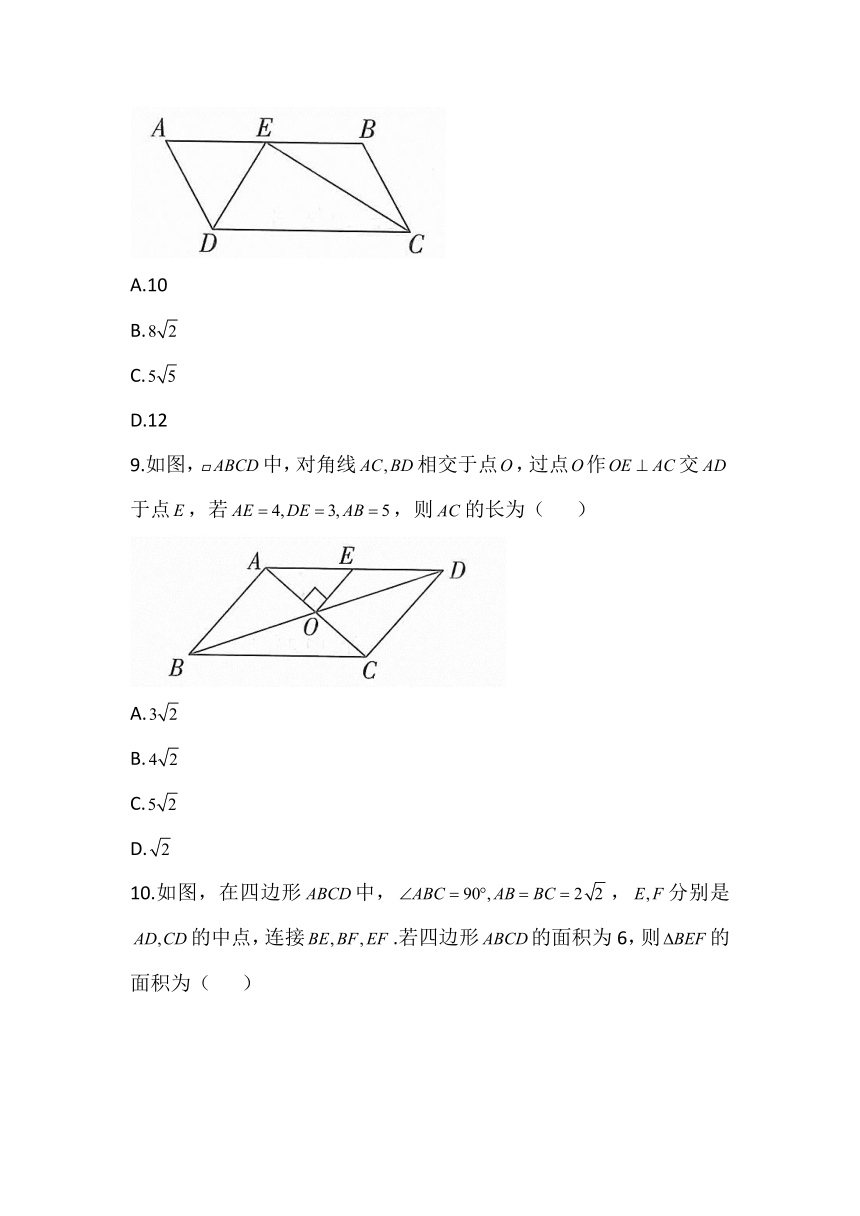
8.如图,在平行四边形中,点是边上一点,连接,.若分别是的平分线,且,则平行四边形的周长为( )
A.10
B.
C.
D.12
9.如图,中,对角线相交于点,过点作交于点,若,则的长为( )
A.
B.
C.
D.
10.如图,在四边形中,,分别是的中点,连接.若四边形的面积为6,则的面积为( )
A.2
B.
C.
D.3
二、填空题(每题2分,共20分)
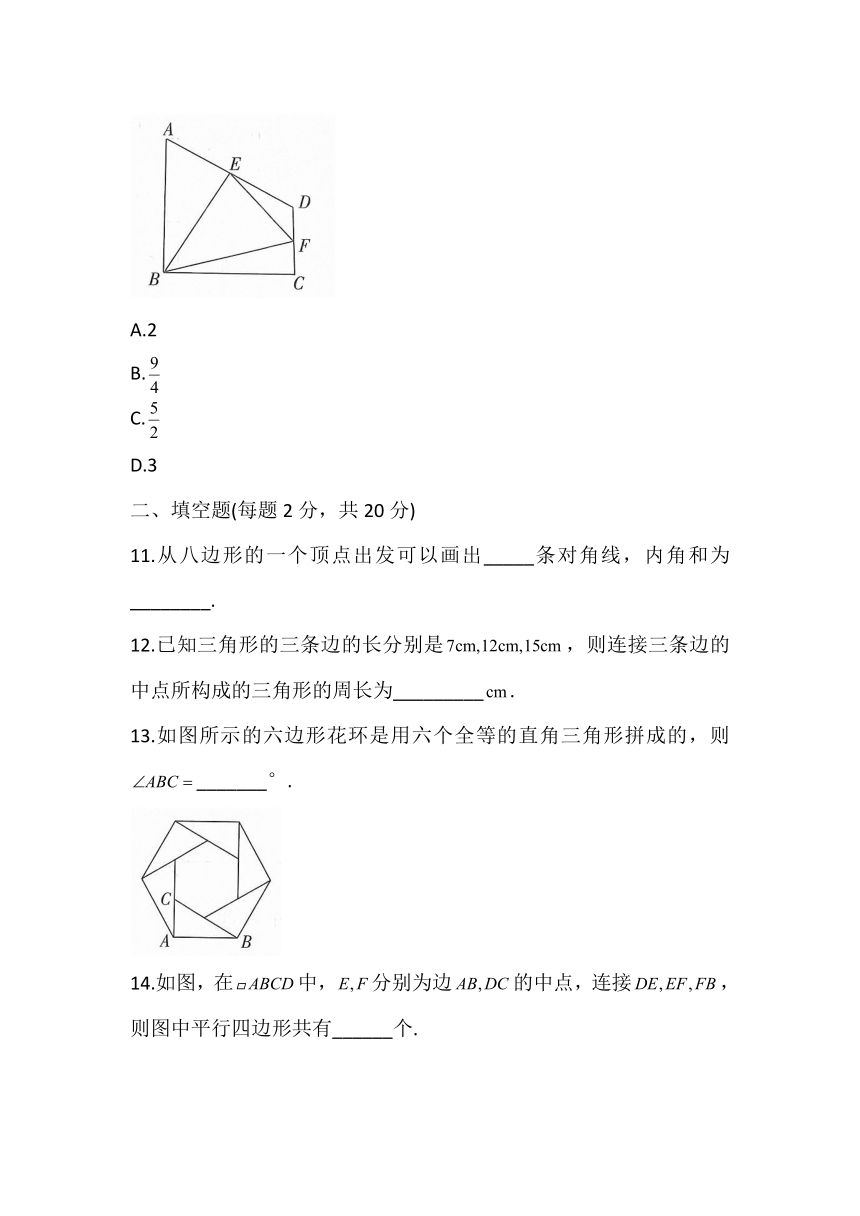
11.从八边形的一个顶点出发可以画出_____条对角线,内角和为________.
12.已知三角形的三条边的长分别是,则连接三条边的中点所构成的三角形的周长为_________.
13.如图所示的六边形花环是用六个全等的直角三角形拼成的,则_______°.
14.如图,在中,分别为边的中点,连接,则图中平行四边形共有______个.
15.如图,点分别是的边的中点,连接,过点作,交的延长线于点,若,则的长为________.
16.如图,将一张直角三角形纸片沿中位线剪开后,在平面上将绕着的中点逆时针旋转,点到了点的位置,则四边形的形状是_________.
17.已知,在中,的平分线分成和两条线段,则的周长为_________.
18.如图,在中,,于点,于点,与交于点,则的度数为________.
19.如图,在四边形中,点是对角线的中点,点分别是的中点,,则的度数是______.
20.如图,__________°.
三、解答题(共50分)
21.(9分)如图,在四边形中,和是它的两条对角线,分别为的中点,分别为的中点.求证:与互相平分.
22.(10分)如图,是的边的中点,延长交的延长线于点.
(1)求证:;
(2)若,求的长.
23.(15分)如图,在四边形中,,与交于点,点是的中点,延长到点,使,连接.
(1)求证:;
(2)求证:四边形是平行四边形;
(3)若,则四边形的面积为_________.
24.(16分)(2020 重庆沙坪坝区校级月考)如图,在平行四边形中,是对角线的中点,过点作交于点.过点作分别交于点.
(1)如图,若,求平行四边形的面积;
(2)连接,如图,若,求证:.
参考答案
1.答案:D
2.答案:C
3.答案:A
4.答案:D
5.答案:D
6.答案:C
7.答案:C
8.答案:D
9.答案:B
10.答案:C
11.答案:5 1080°
12.答案:17
13.答案:30
14.答案:4
15.答案:
16.答案:平行四边形
17.答案:22cm或20cm
18.答案:61°
19.答案:120°
20.答案:180
21.答案:见解析
解析:证明:如答图,连接GN,NH,HM,MG.
∵G,M分别为BD,AD的中点,
∴GM是△ABD的中位线,
∴GM∥AB,GM=AB.
又∵H,N分别为AC,BC的中点,
∴HN为△ABC的中位线,
∴HN∥AB,HN=AB.
∴GM∥HN,GM=HN,
∴四边形GNHM为平行四边形,
∴MN与GH互相平分.
22.答案:见解析
解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥BF,
∴∠DAE=∠F,∠D=∠ECF
∵E是CD的中点,
∴DE=CE,∴△ADE≌△FCE.
(2)解:∵△ADE≌△FCE,EF=3,
∴AE=EF=3.
∵四边形ABCD是平行四边形,∠BAF=90°,BC=5,
∴AB∥CD,AD=BC=5,
∴∠AED=∠BAF=90°
在Rt△AED中,AD=5,AE=3,由勾股定理得
∴
∴CD=2DE=8.
23.答案:见解析
解析:(1)证明:∵E是BD的中点,∴BE=DE.
∵AD∥BC,∴∠ADE=∠CBE.
在△ADE和△CBE中,
∴△ADE≌△CBE(ASA),
∴AE=CE.
(2)证明:∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CD,∴DF=AB.
又DF∥AB,
∴四边形ABDF是平行四边形.
(3)6
24.答案:见解析
解析:(1)解:连接BD,如下图.
∵四边形为平行四边形,为对角线的中
点,∴过点,且,
∴.
∵,
∴平行四边形的面积.
(2)证明:过点作,与的延长线交于点,如答图.
∵OE⊥BC,
∴∠OEG+∠GEC=∠GEC+∠CEH=90°,
∴∠OEG=∠CEH.
∵∠ACB=45°,∴∠COE=45°,
∴OE=CE.
∵四边形ABCD为平行四边形,∴AB∥CD,
又FG⊥AB,∴FG⊥CD,
∴∠EOG+∠ECG=360°-90°-90°=180°,
∵∠ECH+∠ECG=180°,
∴∠EOG=∠ECH,
∴△OEG≌△CEH(ASA),
∴OG=CH,EG=EH,
∵四边形ABCD是平行四边形,∴OA=OC.
∵AB∥CD,∴∠OAF=∠OCG,
∵∠AOF=∠COG,∴△OAF≌△OCG(ASA),
∴AF=CG,OF=OG,
∵CG+CH=GH,∴AF+OF=GH,
一、选择题
1.若一个正多边形的一个外角是,则该正多边形的内角和为( )
A.
B.
C.
D.
2.如图,将一副三角板在平行四边形中作如下摆放,,那么的度数为( )
A.
B.
C.
D.
3.如图,的周长为52,对角线相交于点,点是CD的中点,BD=18,则△DOE的周长是( )
A.22
B.26
C.31
D.35
4.如图,直线,点分别在直线上,,若点在直线上,,且直线和之间的距离为3,则线段的长度为( )
A.
B.
C.3
D.6
5.如图,在平行四边形中,,为上一点,为的中点,则下列结论中正确的是( )
A.
B.
C.
D.
6.如图,在□ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2:3,平行四边形ABCD的周长为40,则AB的长为( )
A.12
B.9
C.8
D.6
7.如图,在中,,的平分线交于点,交的延长线于点,则的长为( )
A.4
B.2
C.3
D.
8.如图,在平行四边形中,点是边上一点,连接,.若分别是的平分线,且,则平行四边形的周长为( )
A.10
B.
C.
D.12
9.如图,中,对角线相交于点,过点作交于点,若,则的长为( )
A.
B.
C.
D.
10.如图,在四边形中,,分别是的中点,连接.若四边形的面积为6,则的面积为( )
A.2
B.
C.
D.3
二、填空题(每题2分,共20分)
11.从八边形的一个顶点出发可以画出_____条对角线,内角和为________.
12.已知三角形的三条边的长分别是,则连接三条边的中点所构成的三角形的周长为_________.
13.如图所示的六边形花环是用六个全等的直角三角形拼成的,则_______°.
14.如图,在中,分别为边的中点,连接,则图中平行四边形共有______个.
15.如图,点分别是的边的中点,连接,过点作,交的延长线于点,若,则的长为________.
16.如图,将一张直角三角形纸片沿中位线剪开后,在平面上将绕着的中点逆时针旋转,点到了点的位置,则四边形的形状是_________.
17.已知,在中,的平分线分成和两条线段,则的周长为_________.
18.如图,在中,,于点,于点,与交于点,则的度数为________.
19.如图,在四边形中,点是对角线的中点,点分别是的中点,,则的度数是______.
20.如图,__________°.
三、解答题(共50分)
21.(9分)如图,在四边形中,和是它的两条对角线,分别为的中点,分别为的中点.求证:与互相平分.
22.(10分)如图,是的边的中点,延长交的延长线于点.
(1)求证:;
(2)若,求的长.
23.(15分)如图,在四边形中,,与交于点,点是的中点,延长到点,使,连接.
(1)求证:;
(2)求证:四边形是平行四边形;
(3)若,则四边形的面积为_________.
24.(16分)(2020 重庆沙坪坝区校级月考)如图,在平行四边形中,是对角线的中点,过点作交于点.过点作分别交于点.
(1)如图,若,求平行四边形的面积;
(2)连接,如图,若,求证:.
参考答案
1.答案:D
2.答案:C
3.答案:A
4.答案:D
5.答案:D
6.答案:C
7.答案:C
8.答案:D
9.答案:B
10.答案:C
11.答案:5 1080°
12.答案:17
13.答案:30
14.答案:4
15.答案:
16.答案:平行四边形
17.答案:22cm或20cm
18.答案:61°
19.答案:120°
20.答案:180
21.答案:见解析
解析:证明:如答图,连接GN,NH,HM,MG.
∵G,M分别为BD,AD的中点,
∴GM是△ABD的中位线,
∴GM∥AB,GM=AB.
又∵H,N分别为AC,BC的中点,
∴HN为△ABC的中位线,
∴HN∥AB,HN=AB.
∴GM∥HN,GM=HN,
∴四边形GNHM为平行四边形,
∴MN与GH互相平分.
22.答案:见解析
解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥BF,
∴∠DAE=∠F,∠D=∠ECF
∵E是CD的中点,
∴DE=CE,∴△ADE≌△FCE.
(2)解:∵△ADE≌△FCE,EF=3,
∴AE=EF=3.
∵四边形ABCD是平行四边形,∠BAF=90°,BC=5,
∴AB∥CD,AD=BC=5,
∴∠AED=∠BAF=90°
在Rt△AED中,AD=5,AE=3,由勾股定理得
∴
∴CD=2DE=8.
23.答案:见解析
解析:(1)证明:∵E是BD的中点,∴BE=DE.
∵AD∥BC,∴∠ADE=∠CBE.
在△ADE和△CBE中,
∴△ADE≌△CBE(ASA),
∴AE=CE.
(2)证明:∵AE=CE,BE=DE,
∴四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CD,∴DF=AB.
又DF∥AB,
∴四边形ABDF是平行四边形.
(3)6
24.答案:见解析
解析:(1)解:连接BD,如下图.
∵四边形为平行四边形,为对角线的中
点,∴过点,且,
∴.
∵,
∴平行四边形的面积.
(2)证明:过点作,与的延长线交于点,如答图.
∵OE⊥BC,
∴∠OEG+∠GEC=∠GEC+∠CEH=90°,
∴∠OEG=∠CEH.
∵∠ACB=45°,∴∠COE=45°,
∴OE=CE.
∵四边形ABCD为平行四边形,∴AB∥CD,
又FG⊥AB,∴FG⊥CD,
∴∠EOG+∠ECG=360°-90°-90°=180°,
∵∠ECH+∠ECG=180°,
∴∠EOG=∠ECH,
∴△OEG≌△CEH(ASA),
∴OG=CH,EG=EH,
∵四边形ABCD是平行四边形,∴OA=OC.
∵AB∥CD,∴∠OAF=∠OCG,
∵∠AOF=∠COG,∴△OAF≌△OCG(ASA),
∴AF=CG,OF=OG,
∵CG+CH=GH,∴AF+OF=GH,
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
