人教版七年级上册1.2.4 绝对值课件(共15张PPT)
文档属性
| 名称 | 人教版七年级上册1.2.4 绝对值课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 691.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 10:34:13 | ||
图片预览





文档简介
(共15张PPT)
1.2.4 绝对值
第一章 有理数
学习目标
1.理解绝对值的概念和性质。
2.会求一个有理数的绝对值。
3.能对绝对值进行计算。
新课导入
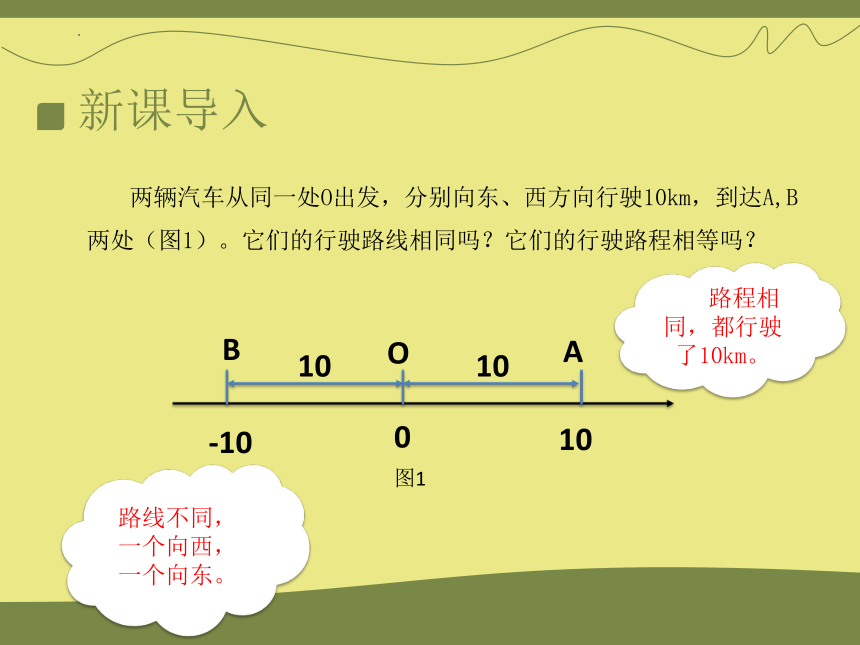
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A,B两处(图1)。它们的行驶路线相同吗?它们的行驶路程相等吗?
B
O
A
10
10
-10
10
0
路线不同,一个向西,一个向东。
路程相同,都行驶了10km。
图1
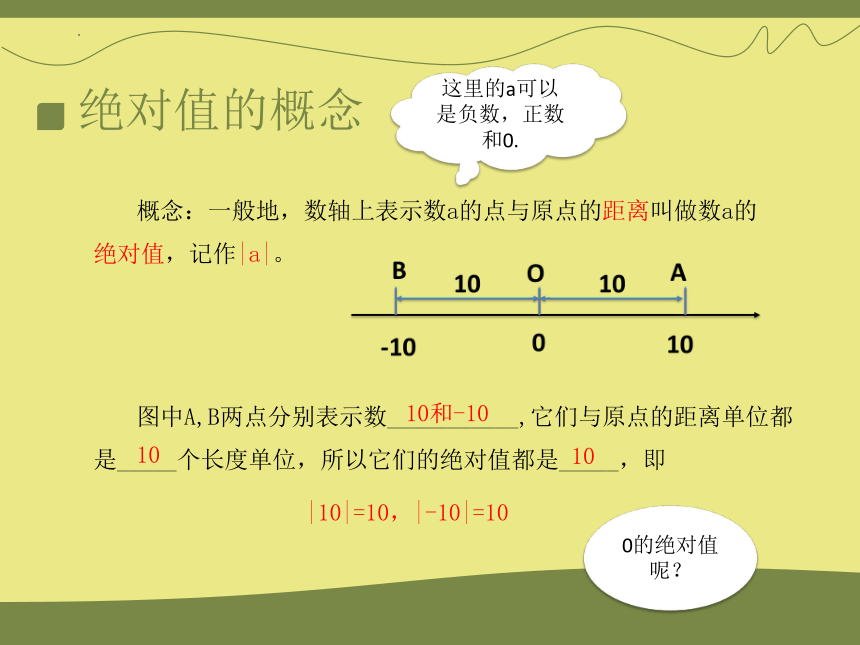
绝对值的概念
概念:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
图中A,B两点分别表示数___________,它们与原点的距离单位都是_____个长度单位,所以它们的绝对值都是_____,即
|10|=10,|-10|=10
0的绝对值呢?
10和-10
10
10
这里的a可以是负数,正数和0.
课堂练习
1.写出下列各数的绝对值:
9,-10,-7.9,,-,120,0
|9|=9 |-10}=10 |-7.9|=7.9
||=|-|=|-| |120|=120 |0|=0
结合该题,你能发现什么规律?
绝对值的概念
有绝对值的定义可知:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
(1)如果a>0,那么|a|=a;
(2)如果a=0,那么|a|=0;
(3)如果a<0,那么|a|=-a.
同学们能用字母a表示吗?
课堂练习
2.判断题:
(1)符号相反的数互为相反数( )
(2)一个数的绝对值越大,表示它的点在数轴上越靠右( )
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远( )
(4)当a≠0时,|a|总是大于0( )
(5)|8|=|-8|( ) (6)-|8|=|-8|( )
(7)-8=|-8|( )
√
×
√
√
√
×
×
绝对值的性质
(1)有没有绝对值等于-9的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
绝对值的性质:不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有|a|≥0
经典例题
图2给出了未来一周中每天的最高气温和最低气温,其中最低气温是多少 最高气温呢 你能将这七天中每天的最低气温按从低到高的顺序排列吗 并画在数轴上。
图2
解:从低到高排列为
-4,-3,-2,-1,0,1,2
-4 -3 -2 -1 0 1 2
归纳总结
数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.由这个规定可知.
-6<-5,-5<-4, -4<-3,-2<0, -1<1, ..
对于正数、0和负数这三类数,它们之间有什么大小关系?
两个负数之间如何比较大小?前面最低气温由低到高的排列与你的结论一致吗?
归纳总结
一般地,
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小,
例如,1_____0,0____-1,1____-1,-3____-4.
|-3|____|-4| |-9|____|-13|
>
>
>
>
<
<
经典例题
比较下面各组数之间的大小:
(1)-(-9)和-(+10)(2)-和-;;(3)-(-0.5)和|-|
化简,
-(-9)=9
-(+10)=-10
因为正数大于负数,
所以9>-10
即-(-9)>-(+10);
两个负数比大小,
先求绝对值
|-|=,|-|==;
因为 ,
所以--.
化简,
-(-0.5)=0.5
|-|==0.6
因为0.5<,
所以-(-0.5)<|-|
异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
拓展提升
1.已知|x-2|+|y-6|=0,求x+y的值。
解:根据题意可知
x-2=0,y-6=0,
所以x=2,y=6
即x+y=2+6=8
归纳总结:一个数的绝对值总是大于或等于0,也就是非负数,如果几个非负数相加的和为0,那么这几个数都为0.
课堂小结
1.绝对值的定义:数轴上表示数a的点与原点的距离叫做数a的绝对值。
2.绝对值的性质
(1)|a|≥0;
(2)|a|=
a (a>0)
-a (a<0)
0 (a=0)
巩固练习
1.已知|a-9|+|b+8|=0,求a+b的值。
解:根据题意可知
a-9=0,b+8=0,
所以a=9,b=-8
即a+b=9-8=1
1.2.4 绝对值
第一章 有理数
学习目标
1.理解绝对值的概念和性质。
2.会求一个有理数的绝对值。
3.能对绝对值进行计算。
新课导入
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A,B两处(图1)。它们的行驶路线相同吗?它们的行驶路程相等吗?
B
O
A
10
10
-10
10
0
路线不同,一个向西,一个向东。
路程相同,都行驶了10km。
图1
绝对值的概念
概念:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
图中A,B两点分别表示数___________,它们与原点的距离单位都是_____个长度单位,所以它们的绝对值都是_____,即
|10|=10,|-10|=10
0的绝对值呢?
10和-10
10
10
这里的a可以是负数,正数和0.
课堂练习
1.写出下列各数的绝对值:
9,-10,-7.9,,-,120,0
|9|=9 |-10}=10 |-7.9|=7.9
||=|-|=|-| |120|=120 |0|=0
结合该题,你能发现什么规律?
绝对值的概念
有绝对值的定义可知:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
(1)如果a>0,那么|a|=a;
(2)如果a=0,那么|a|=0;
(3)如果a<0,那么|a|=-a.
同学们能用字母a表示吗?
课堂练习
2.判断题:
(1)符号相反的数互为相反数( )
(2)一个数的绝对值越大,表示它的点在数轴上越靠右( )
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远( )
(4)当a≠0时,|a|总是大于0( )
(5)|8|=|-8|( ) (6)-|8|=|-8|( )
(7)-8=|-8|( )
√
×
√
√
√
×
×
绝对值的性质
(1)有没有绝对值等于-9的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
绝对值的性质:不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有|a|≥0
经典例题
图2给出了未来一周中每天的最高气温和最低气温,其中最低气温是多少 最高气温呢 你能将这七天中每天的最低气温按从低到高的顺序排列吗 并画在数轴上。
图2
解:从低到高排列为
-4,-3,-2,-1,0,1,2
-4 -3 -2 -1 0 1 2
归纳总结
数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.由这个规定可知.
-6<-5,-5<-4, -4<-3,-2<0, -1<1, ..
对于正数、0和负数这三类数,它们之间有什么大小关系?
两个负数之间如何比较大小?前面最低气温由低到高的排列与你的结论一致吗?
归纳总结
一般地,
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小,
例如,1_____0,0____-1,1____-1,-3____-4.
|-3|____|-4| |-9|____|-13|
>
>
>
>
<
<
经典例题
比较下面各组数之间的大小:
(1)-(-9)和-(+10)(2)-和-;;(3)-(-0.5)和|-|
化简,
-(-9)=9
-(+10)=-10
因为正数大于负数,
所以9>-10
即-(-9)>-(+10);
两个负数比大小,
先求绝对值
|-|=,|-|==;
因为 ,
所以--.
化简,
-(-0.5)=0.5
|-|==0.6
因为0.5<,
所以-(-0.5)<|-|
异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
拓展提升
1.已知|x-2|+|y-6|=0,求x+y的值。
解:根据题意可知
x-2=0,y-6=0,
所以x=2,y=6
即x+y=2+6=8
归纳总结:一个数的绝对值总是大于或等于0,也就是非负数,如果几个非负数相加的和为0,那么这几个数都为0.
课堂小结
1.绝对值的定义:数轴上表示数a的点与原点的距离叫做数a的绝对值。
2.绝对值的性质
(1)|a|≥0;
(2)|a|=
a (a>0)
-a (a<0)
0 (a=0)
巩固练习
1.已知|a-9|+|b+8|=0,求a+b的值。
解:根据题意可知
a-9=0,b+8=0,
所以a=9,b=-8
即a+b=9-8=1
