人教版七年级下册5相交线与平行线课件(共17张PPT)
文档属性
| 名称 | 人教版七年级下册5相交线与平行线课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 90.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
致亲爱的我们
面对现实,逆境也会变为顺境,总有转机的机会。逃避现实,虽暂时偷安,但没有翻身余地。就像学习一样,遇到不会的题,要迎难而上,勇敢地去面对。战略上藐视它,战术上重视它。
第五章
相交线与平行线
复习
学习目标
掌握对顶角、邻补角的概念及性质;
2. 熟练掌握垂线、点到直线的距离的有关知识;
3. 会灵活运用相交与平行的有关性质
解决实际问题。
相交线
两条直线相交
邻补角、对顶角
垂线及其性质
点到直线的距离
两条直线被第三条直线所截
同位角、内错角、
同旁内角
平行线
平行公理
平移
判定
性质
本章知识结构
b
a
)
(
1
3
4
2
)
(
专题一 对顶角邻补角专题
例1 如图,直线a、b相交,∠1=40°,
求 ∠2、∠3、∠4的度数。
(对顶角相等)
∵∠1=40°( )
已知
∴∠3= ∠1=40°
解:
∴∠2=180°—∠1=140°
∴∠4=∠2=140°
(对顶角相等)
(邻补角的定义)
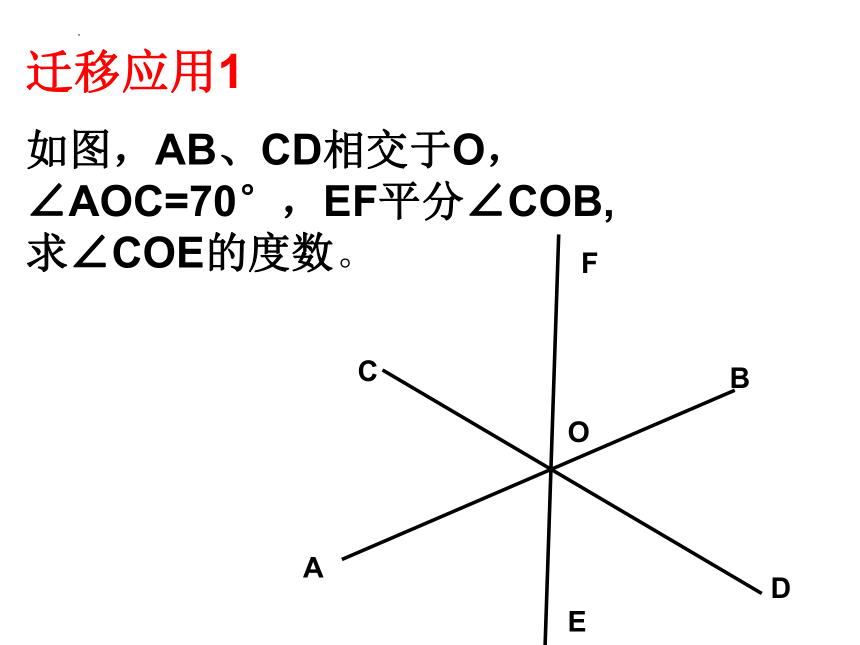
迁移应用1
如图,AB、CD相交于O,∠AOC=70°,EF平分∠COB,求∠COE的度数。
O
A
B
C
D
E
F
专题二 点到直线的距离
例2 如图,
过点D分别画OA、OB的垂线。
A
B
O
D
迁移应用2
如图,AC⊥BC,CD⊥AB于D,CD=4.8cm,AC=6cm,BC=8cm,
则点C到AB的距离是 cm;
点A到BC的距离是 cm;
点B到AC的距离是 cm.
A
D
B
C
6
8
4.8
迁移应用2
如图所示,能表示点到直线(线段)的距离的线段有( )条
A
B
C
D
3
F
E
D
A
B
C
专题三 平行线判定及性质
例3 如图:已知: ∠A=∠D ∠C=∠F ,
问: CE与BF平行吗?为什么?
迁移应用3
把一个长方形纸片沿EF折叠后,
点D,C分别落在D′,C′的位置上,
若∠EFB=65°,则∠AED′是多少度?
A
B
D
C
E
F
C′
D′
∠AED′= 50°
专题四 命题专题
例4 命题“同旁内角互补”的
题设是
结论是
两个角是同旁内角
这两个角互补
迁移应用4
下面的四个命题中,真命题是( )
A.相等的角是对顶角;
B.和为180°的两个角互为邻补角;
C.两条直线相交形成的四个角相等,
则这两条直线互相垂直;
D.两条直线被第三条直线所截,
内错角相等。
C
专题五 平移
如图,将直角三角形ABC沿CB方向
平移BE的距离后得到直角三角形DEF,
已知 AG=2,BE=4,DE=6,
求阴影部分的面积。
A
C
D
E
B
F
G
例5
20
课堂小结
1.知识小结
对顶角、邻补角、垂线、同位角、内错角、
同旁内角、平行线判定和性质、命题、平移
2.解题小结
数学建模:将实际问题抽象为数学问题
数学思想:转化的数学思想
数学规律
3月1日课堂作业
1.如图,AB∥CD,
试说明∠B、∠D 、∠BED之间的大小关系。
A
B
C
D
E
F
A
B
C
D
E
1
2
2.如图,E、A、B在一条直线上,AD∥BC,AD平分∠EAC,
试判定∠B与∠C的大小关系。
致亲爱的我们
面对现实,逆境也会变为顺境,总有转机的机会。逃避现实,虽暂时偷安,但没有翻身余地。就像学习一样,遇到不会的题,要迎难而上,勇敢地去面对。战略上藐视它,战术上重视它。
第五章
相交线与平行线
复习
学习目标
掌握对顶角、邻补角的概念及性质;
2. 熟练掌握垂线、点到直线的距离的有关知识;
3. 会灵活运用相交与平行的有关性质
解决实际问题。
相交线
两条直线相交
邻补角、对顶角
垂线及其性质
点到直线的距离
两条直线被第三条直线所截
同位角、内错角、
同旁内角
平行线
平行公理
平移
判定
性质
本章知识结构
b
a
)
(
1
3
4
2
)
(
专题一 对顶角邻补角专题
例1 如图,直线a、b相交,∠1=40°,
求 ∠2、∠3、∠4的度数。
(对顶角相等)
∵∠1=40°( )
已知
∴∠3= ∠1=40°
解:
∴∠2=180°—∠1=140°
∴∠4=∠2=140°
(对顶角相等)
(邻补角的定义)
迁移应用1
如图,AB、CD相交于O,∠AOC=70°,EF平分∠COB,求∠COE的度数。
O
A
B
C
D
E
F
专题二 点到直线的距离
例2 如图,
过点D分别画OA、OB的垂线。
A
B
O
D
迁移应用2
如图,AC⊥BC,CD⊥AB于D,CD=4.8cm,AC=6cm,BC=8cm,
则点C到AB的距离是 cm;
点A到BC的距离是 cm;
点B到AC的距离是 cm.
A
D
B
C
6
8
4.8
迁移应用2
如图所示,能表示点到直线(线段)的距离的线段有( )条
A
B
C
D
3
F
E
D
A
B
C
专题三 平行线判定及性质
例3 如图:已知: ∠A=∠D ∠C=∠F ,
问: CE与BF平行吗?为什么?
迁移应用3
把一个长方形纸片沿EF折叠后,
点D,C分别落在D′,C′的位置上,
若∠EFB=65°,则∠AED′是多少度?
A
B
D
C
E
F
C′
D′
∠AED′= 50°
专题四 命题专题
例4 命题“同旁内角互补”的
题设是
结论是
两个角是同旁内角
这两个角互补
迁移应用4
下面的四个命题中,真命题是( )
A.相等的角是对顶角;
B.和为180°的两个角互为邻补角;
C.两条直线相交形成的四个角相等,
则这两条直线互相垂直;
D.两条直线被第三条直线所截,
内错角相等。
C
专题五 平移
如图,将直角三角形ABC沿CB方向
平移BE的距离后得到直角三角形DEF,
已知 AG=2,BE=4,DE=6,
求阴影部分的面积。
A
C
D
E
B
F
G
例5
20
课堂小结
1.知识小结
对顶角、邻补角、垂线、同位角、内错角、
同旁内角、平行线判定和性质、命题、平移
2.解题小结
数学建模:将实际问题抽象为数学问题
数学思想:转化的数学思想
数学规律
3月1日课堂作业
1.如图,AB∥CD,
试说明∠B、∠D 、∠BED之间的大小关系。
A
B
C
D
E
F
A
B
C
D
E
1
2
2.如图,E、A、B在一条直线上,AD∥BC,AD平分∠EAC,
试判定∠B与∠C的大小关系。
