湘教版数学七年级下册 4.4 平行线的判定 同步练习(word,含答案)
文档属性
| 名称 | 湘教版数学七年级下册 4.4 平行线的判定 同步练习(word,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 12:09:55 | ||
图片预览

文档简介
4.4 平行线的判定
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.(2013·永州中考)如图,下列条件中能判定直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5
C.∠1+∠3=180° D.∠3=∠5
2.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠D=∠DCE
C.∠1=∠2 D.∠D+∠ACD=180°
3.(2013·恩施中考)如图,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
二、填空题(每小题4分,共12分)
4.如图,已知∠1=∠2,∠B=40°,则∠3= .
5.如图,∠1=∠2,要判断AB∥DF,需要增加条件 .
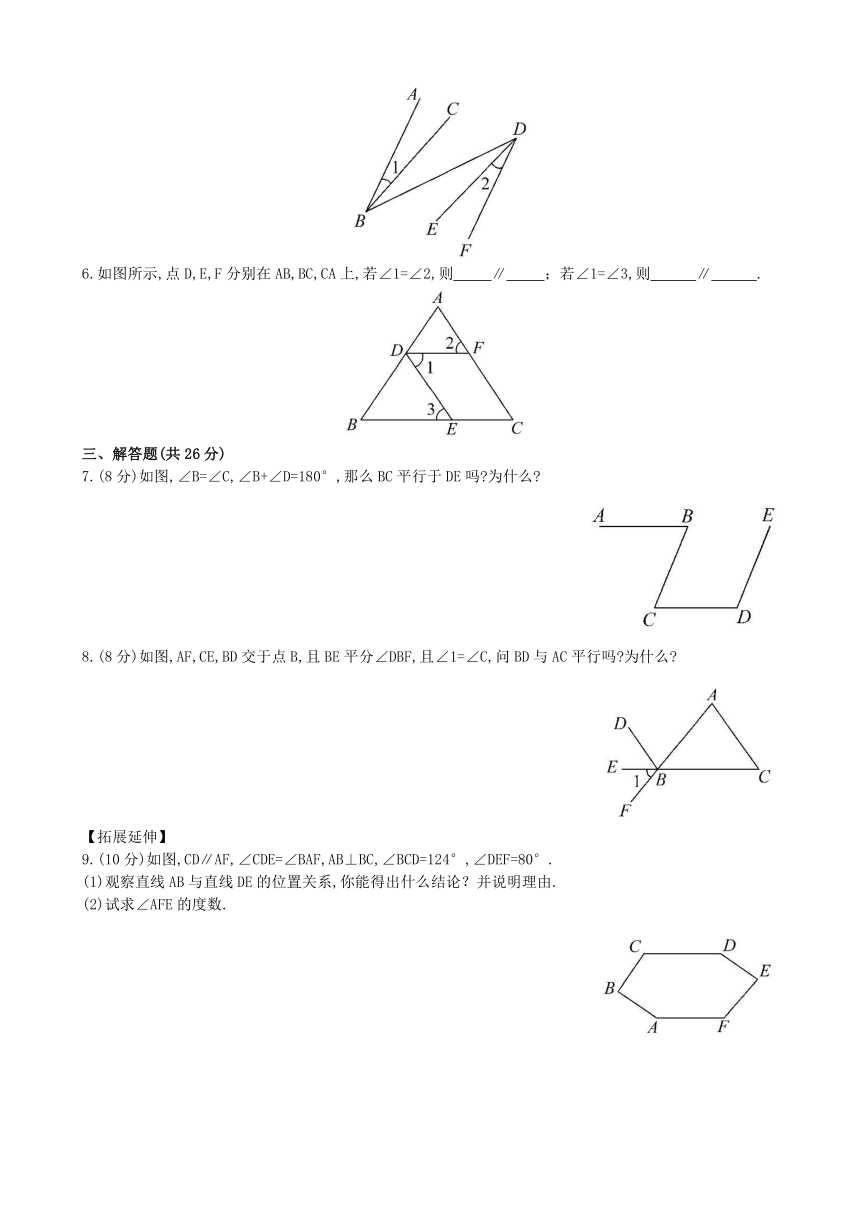
6.如图所示,点D,E,F分别在AB,BC,CA上,若∠1=∠2,则 ∥ ;若∠1=∠3,则 ∥ .
三、解答题(共26分)
7.(8分)如图,∠B=∠C,∠B+∠D=180°,那么BC平行于DE吗 为什么
8.(8分)如图,AF,CE,BD交于点B,且BE平分∠DBF,且∠1=∠C,问BD与AC平行吗 为什么
【拓展延伸】
9.(10分)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
(1)观察直线AB与直线DE的位置关系,你能得出什么结论?并说明理由.
(2)试求∠AFE的度数.
参考答案
1.C 【解析】因为∠1+∠3=180°,所以l1∥l2(同旁内角互补,两直线平行).
2.C 【解析】因为∠1=∠2,所以AB∥CD(内错角相等,两直线平行).
3.D 【解析】如图,因为∠1+∠2=180°,∠1+∠5=180°,所以∠2=∠5,所以a∥b,所以∠4=∠6.因为∠3=∠6,∠3=100°,所以∠4=100°.
4.40° 【解析】因为∠1=∠2,所以AB∥EC,所以∠3=∠B=40°.
5.∠ABD=∠BDF(或∠CBD=∠BDE) 【解析】欲使AB∥DF,只需∠ABD=∠BDF,故可添加∠ABD=∠BDF,或∠CBD=
∠BDE.
6.AC DE DF BC 【解析】∠1和∠2是AC,DE被DF所截的内错角,又因为∠1=∠2,所以AC∥DE;同理得DF∥BC.
7.解:BC∥DE.
理由:因为∠B=∠C,∠B+∠D=180°,
所以∠C+∠D=180°(等量代换).
所以BC∥DE(同旁内角互补,两直线平行).
8.解:BD∥AC.
理由:因为BE平分∠DBF,
所以∠1=∠EBD(角平分线的定义).
因为∠1=∠C,
所以∠C=∠EBD(等量代换),
所以BD∥AC(同位角相等,两直线平行).
9.解:(1)AB∥DE.
理由:延长AF,DE相交于点G,
因为CD∥AF,所以∠CDE+∠G=180°.
因为∠CDE=∠BAF,
所以∠BAF+∠G=180°,
所以AB∥DE.
(2)延长BC,ED相交于点H.
因为AB⊥BC,所以∠B=90°.
因为AB∥DE,所以∠H+∠B=180°,
所以∠H=90°.
因为∠BCD=124°,所以∠DCH=56°,
所以∠CDH=34°,所以∠G=∠CDH=34°.
因为∠DEF=80°,所以∠EFG=80°-34°=46°,
所以∠AFE=180°-∠EFG=180°-46°=134°.
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.(2013·永州中考)如图,下列条件中能判定直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5
C.∠1+∠3=180° D.∠3=∠5
2.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠D=∠DCE
C.∠1=∠2 D.∠D+∠ACD=180°
3.(2013·恩施中考)如图,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
二、填空题(每小题4分,共12分)
4.如图,已知∠1=∠2,∠B=40°,则∠3= .
5.如图,∠1=∠2,要判断AB∥DF,需要增加条件 .
6.如图所示,点D,E,F分别在AB,BC,CA上,若∠1=∠2,则 ∥ ;若∠1=∠3,则 ∥ .
三、解答题(共26分)
7.(8分)如图,∠B=∠C,∠B+∠D=180°,那么BC平行于DE吗 为什么
8.(8分)如图,AF,CE,BD交于点B,且BE平分∠DBF,且∠1=∠C,问BD与AC平行吗 为什么
【拓展延伸】
9.(10分)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
(1)观察直线AB与直线DE的位置关系,你能得出什么结论?并说明理由.
(2)试求∠AFE的度数.
参考答案
1.C 【解析】因为∠1+∠3=180°,所以l1∥l2(同旁内角互补,两直线平行).
2.C 【解析】因为∠1=∠2,所以AB∥CD(内错角相等,两直线平行).
3.D 【解析】如图,因为∠1+∠2=180°,∠1+∠5=180°,所以∠2=∠5,所以a∥b,所以∠4=∠6.因为∠3=∠6,∠3=100°,所以∠4=100°.
4.40° 【解析】因为∠1=∠2,所以AB∥EC,所以∠3=∠B=40°.
5.∠ABD=∠BDF(或∠CBD=∠BDE) 【解析】欲使AB∥DF,只需∠ABD=∠BDF,故可添加∠ABD=∠BDF,或∠CBD=
∠BDE.
6.AC DE DF BC 【解析】∠1和∠2是AC,DE被DF所截的内错角,又因为∠1=∠2,所以AC∥DE;同理得DF∥BC.
7.解:BC∥DE.
理由:因为∠B=∠C,∠B+∠D=180°,
所以∠C+∠D=180°(等量代换).
所以BC∥DE(同旁内角互补,两直线平行).
8.解:BD∥AC.
理由:因为BE平分∠DBF,
所以∠1=∠EBD(角平分线的定义).
因为∠1=∠C,
所以∠C=∠EBD(等量代换),
所以BD∥AC(同位角相等,两直线平行).
9.解:(1)AB∥DE.
理由:延长AF,DE相交于点G,
因为CD∥AF,所以∠CDE+∠G=180°.
因为∠CDE=∠BAF,
所以∠BAF+∠G=180°,
所以AB∥DE.
(2)延长BC,ED相交于点H.
因为AB⊥BC,所以∠B=90°.
因为AB∥DE,所以∠H+∠B=180°,
所以∠H=90°.
因为∠BCD=124°,所以∠DCH=56°,
所以∠CDH=34°,所以∠G=∠CDH=34°.
因为∠DEF=80°,所以∠EFG=80°-34°=46°,
所以∠AFE=180°-∠EFG=180°-46°=134°.
