2.3.1抛物线及其标准方程(人教版选修1-1)
文档属性
| 名称 | 2.3.1抛物线及其标准方程(人教版选修1-1) |  | |
| 格式 | zip | ||
| 文件大小 | 387.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-05 10:06:49 | ||
图片预览







文档简介
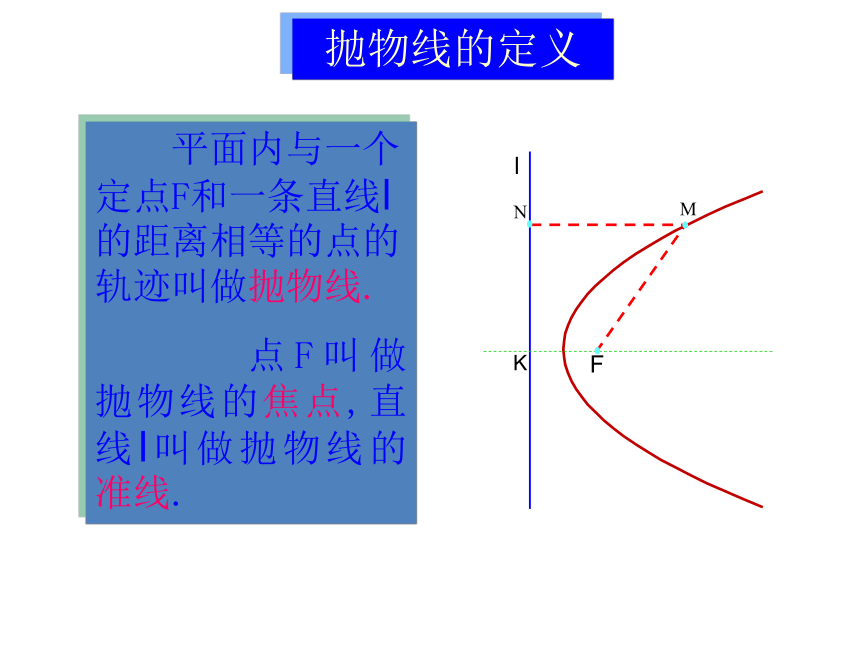
课件21张PPT。2.3.1抛物线及其标准方程抛物线的定义 平面内与一个定点F和一条直线l的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线l叫做抛物线的准线.
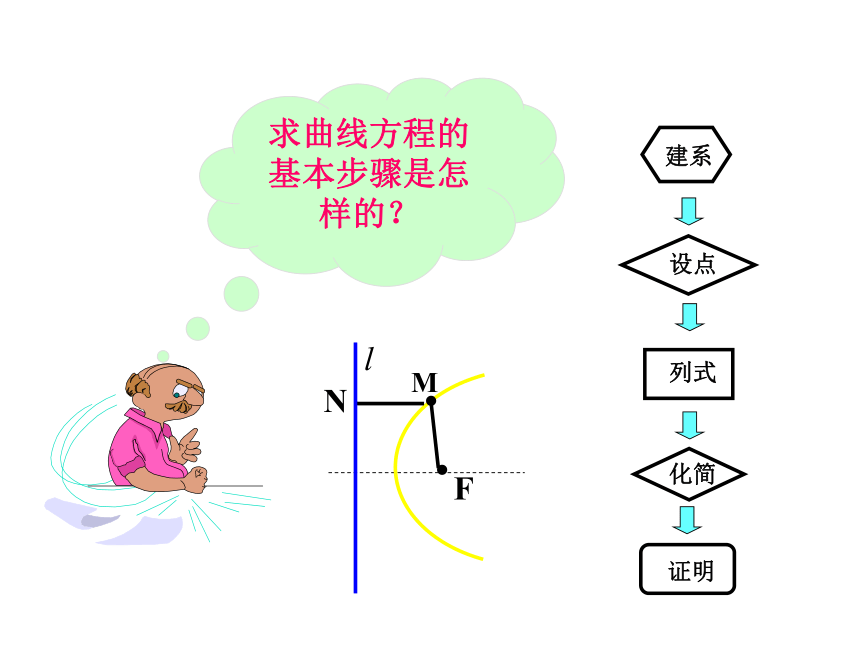
思考 ?类比椭圆、双曲线标准方程的建立过程,你认为如何选择坐标系,建立抛物线
的方程?lFKMN求曲线方程的基本步骤是怎样的?l抛物线方程的推导过程 设一个定点F到一条定直线l的距离为常数p(p>0),如何建立直角坐标系,求出抛物线的方程呢?yoFMN··x解法一:以l为y轴,过点F且垂直于l的直线为x轴
建立直角坐标系,则点F(p ,0).设动点M(x,y),由抛物线定义得设动点M(x,y),由抛物线定义得yKFMN··oxl 解法二:取过点F且垂直于l 的直线为x轴,x轴与l交于K,以线段KF的垂直平分线为y轴建立直角坐标系,焦点F的坐标为(p,0)
准线l的方程为x=0
xyo 方程y2=2px叫做抛物线的标准方程.
它表示焦点在x轴的正半轴上的抛物线,其中焦点坐标是(p/2,0), 准线方程是x=-p/2.抛物线的标准方程其中 p 为正常数,几何意义是
焦 点 到 准 线 的 距 离对“标准”的理解 一般地,我们把顶点在原点、焦点F 在坐标轴上的抛物线的方程叫做抛物线的标准方程.
但是,一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.
yy2 = 2px(p>0)抛物线标准方程的其他形式xyo抛物线的标准方程x2=2py(p>0)(0,p/2)y=-p/2y2=-2px
(p>0)(-p/2,0)x=p/2
x2=-2py
(p>0)(0,-p/2)y=p/2y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2,0)(-p/2,0)y=-p/2x=p/2x=-p/2抛物线的标准方程总结交流填表相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
抛物线标准方程特点:1、 “=”左边是二次项且系数为1,右边是一次项;2、焦点在一次项对应的轴上,
开口方向看一次项系数的正负例题讲解 例1.(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;
(2)已知抛物线经过点(-4,-2),求它的标准方程. 解:(1)因为p=3,所以焦点坐标是(3/2,0),准线方程是x=-3/2.
(2)若抛物线焦点在x轴上,设它的标准方程为y2=2px,由于点(-4,-2)在抛物线上,故有(-2)2=2p(-4),解得p=-1/2,故此时所求标准方程为y2=-x;
若抛物线的焦点在y轴上,设它的标准方程为x2=2py,由于点(-4,-2)在抛物线上,故有(-4)2=2p(-2),解得p=-4,故此时所求标准方程为x2=-8y;
综上所述,满足题意的抛物线的标准方程为
y2=-x或x2=-8y.1. 抛物线的准线方程是x = -4, 则它的标准方程为 . 焦点坐标为 .
2. 抛物线 y = 4x2 的焦点坐标是 .
y2 = 16x(4, 0)课堂练习 思考:试讨论抛物线y = ax2 的开口方向、焦点坐标和准线方程。
总结:课堂小结本节课你有哪些收获?本节课你还有哪些困惑?
点F叫做抛物线的焦点,直线l叫做抛物线的准线.
思考 ?类比椭圆、双曲线标准方程的建立过程,你认为如何选择坐标系,建立抛物线
的方程?lFKMN求曲线方程的基本步骤是怎样的?l抛物线方程的推导过程 设一个定点F到一条定直线l的距离为常数p(p>0),如何建立直角坐标系,求出抛物线的方程呢?yoFMN··x解法一:以l为y轴,过点F且垂直于l的直线为x轴
建立直角坐标系,则点F(p ,0).设动点M(x,y),由抛物线定义得设动点M(x,y),由抛物线定义得yKFMN··oxl 解法二:取过点F且垂直于l 的直线为x轴,x轴与l交于K,以线段KF的垂直平分线为y轴建立直角坐标系,焦点F的坐标为(p,0)
准线l的方程为x=0
xyo 方程y2=2px叫做抛物线的标准方程.
它表示焦点在x轴的正半轴上的抛物线,其中焦点坐标是(p/2,0), 准线方程是x=-p/2.抛物线的标准方程其中 p 为正常数,几何意义是
焦 点 到 准 线 的 距 离对“标准”的理解 一般地,我们把顶点在原点、焦点F 在坐标轴上的抛物线的方程叫做抛物线的标准方程.
但是,一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.
yy2 = 2px(p>0)抛物线标准方程的其他形式xyo抛物线的标准方程x2=2py(p>0)(0,p/2)y=-p/2y2=-2px
(p>0)(-p/2,0)x=p/2
x2=-2py
(p>0)(0,-p/2)y=p/2y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2,0)(-p/2,0)y=-p/2x=p/2x=-p/2抛物线的标准方程总结交流填表相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.相同点
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶
点到准线的距离,其值为p/2.不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
不同点
(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口向坐标轴的正(负)方向.
抛物线标准方程特点:1、 “=”左边是二次项且系数为1,右边是一次项;2、焦点在一次项对应的轴上,
开口方向看一次项系数的正负例题讲解 例1.(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;
(2)已知抛物线经过点(-4,-2),求它的标准方程. 解:(1)因为p=3,所以焦点坐标是(3/2,0),准线方程是x=-3/2.
(2)若抛物线焦点在x轴上,设它的标准方程为y2=2px,由于点(-4,-2)在抛物线上,故有(-2)2=2p(-4),解得p=-1/2,故此时所求标准方程为y2=-x;
若抛物线的焦点在y轴上,设它的标准方程为x2=2py,由于点(-4,-2)在抛物线上,故有(-4)2=2p(-2),解得p=-4,故此时所求标准方程为x2=-8y;
综上所述,满足题意的抛物线的标准方程为
y2=-x或x2=-8y.1. 抛物线的准线方程是x = -4, 则它的标准方程为 . 焦点坐标为 .
2. 抛物线 y = 4x2 的焦点坐标是 .
y2 = 16x(4, 0)课堂练习 思考:试讨论抛物线y = ax2 的开口方向、焦点坐标和准线方程。
总结:课堂小结本节课你有哪些收获?本节课你还有哪些困惑?
