2.2.1《椭圆及其标准方程》(新人教A版选修2-1)
文档属性
| 名称 | 2.2.1《椭圆及其标准方程》(新人教A版选修2-1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-05 10:11:24 | ||
图片预览




文档简介
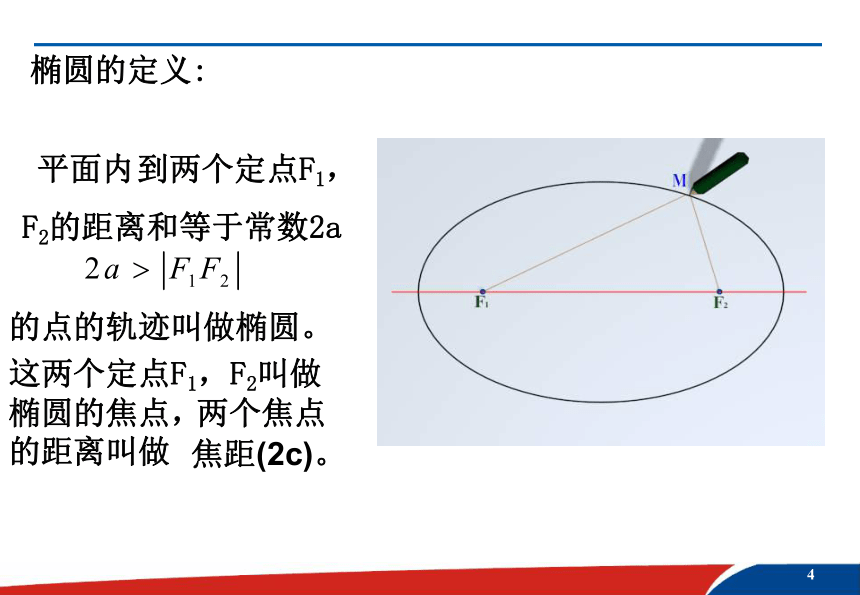
课件18张PPT。椭圆的标准方程椭圆的标准方程椭圆的定义: 到两个定点F1,
F2的距离和等于常数2a平面内这两个定点F1,F2叫做的点的轨迹叫做椭圆。椭圆的焦点, 两个焦点
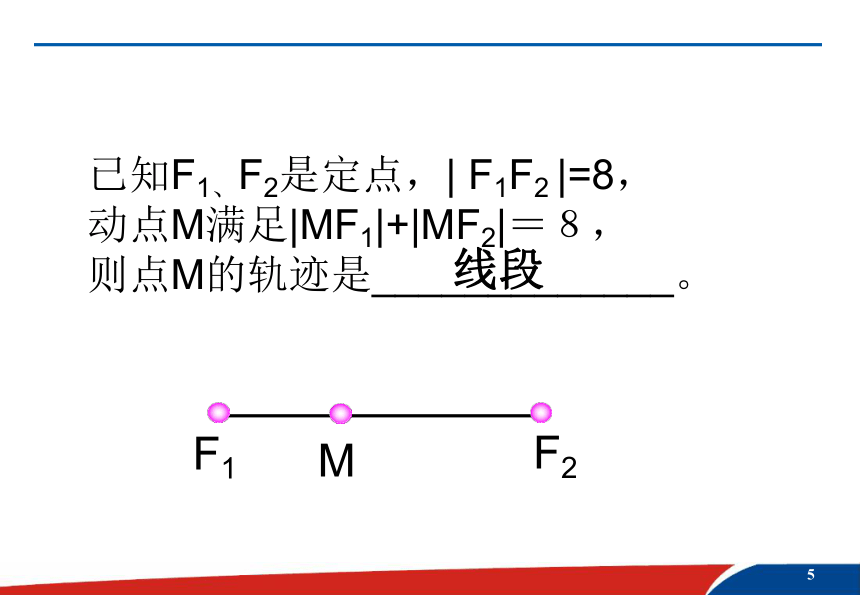
的距离叫做 焦距(2c)。已知F1、F2是定点,| F1F2 |=8,
动点M满足|MF1|+|MF2|=8,
则点M的轨迹是_____________。线段F1F2M在一个平面内,F1F2为两个定点,M为动点|F1F2|=4,|MF1|+|MF2|=2a,若动点M的轨迹为线段F1F2,则2a_______;若动点M的轨迹为椭圆,则2a的取值范围_________。=4(4,+∞)椭圆的标准方程:焦点的位置由什么决定巩固:1、(1)、椭圆: 中,
a=___,b=___,c=___ . (2)、椭圆: 中,
a=___,b=___,c=___.2、椭圆: 的焦距是____.问题:指出下列方程中,哪些是椭圆的方程?若是椭圆的方程,判定椭圆的焦点在哪个轴上,并求焦点坐标.强化:提高: 求椭圆标准方程中共有几个参数?有什么样的关系呢?求下列椭圆的方程:两个焦点的坐标是(-4,0),(4,0),椭圆上一点P到两焦点距离之和为10解:由题意椭圆的焦点在x轴上
所以:设椭圆的方程为
∵2a=10 2c=8
∴a=5 c=4
∴b2=a2-c2=9
∴所求的椭圆的方程为写出适合下列条件的椭圆的标准方程:
①a=4,c=3,焦点在y轴上;
x2/7+y2/16=1
②a=4,b=3,焦点在x轴上;
x2/16+y2/9=1
③a+c=8,b=4
x2/25+y2/16=1或x2/16+y2/25=1
小结:由椭圆定义和标准方程可知,确定椭圆的标准方程需要三个条件:焦点位置,a、b的值。易错辨析:平面内两个定点的距离等于8,一个动点M到这两个定点的距离的和等于10 ,求动点M的轨迹错解:∵2c=8 2a=10
∴c=4 a=5
∴b2=a2-c2=9
∴所以M点的轨迹方程为:1、椭圆的定义、椭圆的标准方程
2、a、b、c之间的关系
3、练习
⑴椭圆x2/5+y2/4=1的焦点坐标是_______;椭圆上任一点P到两焦点的距离和为_____;若该点P到左焦点的距离为1,则点P到右焦点的距离是______。
变:①F1、F2分别是椭圆x2/25+y2/16=1的两个焦点,过F1的直线交椭圆于A、B两点,则ΔF2AB的周长是_______________.
②F1、F2分别是椭圆x2/25+y2/16=1的两个焦点,过F1的直线交椭圆于A、B两点,若|AB|=8,则|F2A|+|F2B|=_______.(±1,0)2012写出适合下列各条件的椭圆的标准方程:
(1)a=4 b=1 焦点在x轴上
(2)a=4 b=3 焦点在y轴上
(3)焦点(0,-4),(0,4)a=5作业:书:习题8.1 1
优化设计
F2的距离和等于常数2a平面内这两个定点F1,F2叫做的点的轨迹叫做椭圆。椭圆的焦点, 两个焦点
的距离叫做 焦距(2c)。已知F1、F2是定点,| F1F2 |=8,
动点M满足|MF1|+|MF2|=8,
则点M的轨迹是_____________。线段F1F2M在一个平面内,F1F2为两个定点,M为动点|F1F2|=4,|MF1|+|MF2|=2a,若动点M的轨迹为线段F1F2,则2a_______;若动点M的轨迹为椭圆,则2a的取值范围_________。=4(4,+∞)椭圆的标准方程:焦点的位置由什么决定巩固:1、(1)、椭圆: 中,
a=___,b=___,c=___ . (2)、椭圆: 中,
a=___,b=___,c=___.2、椭圆: 的焦距是____.问题:指出下列方程中,哪些是椭圆的方程?若是椭圆的方程,判定椭圆的焦点在哪个轴上,并求焦点坐标.强化:提高: 求椭圆标准方程中共有几个参数?有什么样的关系呢?求下列椭圆的方程:两个焦点的坐标是(-4,0),(4,0),椭圆上一点P到两焦点距离之和为10解:由题意椭圆的焦点在x轴上
所以:设椭圆的方程为
∵2a=10 2c=8
∴a=5 c=4
∴b2=a2-c2=9
∴所求的椭圆的方程为写出适合下列条件的椭圆的标准方程:
①a=4,c=3,焦点在y轴上;
x2/7+y2/16=1
②a=4,b=3,焦点在x轴上;
x2/16+y2/9=1
③a+c=8,b=4
x2/25+y2/16=1或x2/16+y2/25=1
小结:由椭圆定义和标准方程可知,确定椭圆的标准方程需要三个条件:焦点位置,a、b的值。易错辨析:平面内两个定点的距离等于8,一个动点M到这两个定点的距离的和等于10 ,求动点M的轨迹错解:∵2c=8 2a=10
∴c=4 a=5
∴b2=a2-c2=9
∴所以M点的轨迹方程为:1、椭圆的定义、椭圆的标准方程
2、a、b、c之间的关系
3、练习
⑴椭圆x2/5+y2/4=1的焦点坐标是_______;椭圆上任一点P到两焦点的距离和为_____;若该点P到左焦点的距离为1,则点P到右焦点的距离是______。
变:①F1、F2分别是椭圆x2/25+y2/16=1的两个焦点,过F1的直线交椭圆于A、B两点,则ΔF2AB的周长是_______________.
②F1、F2分别是椭圆x2/25+y2/16=1的两个焦点,过F1的直线交椭圆于A、B两点,若|AB|=8,则|F2A|+|F2B|=_______.(±1,0)2012写出适合下列各条件的椭圆的标准方程:
(1)a=4 b=1 焦点在x轴上
(2)a=4 b=3 焦点在y轴上
(3)焦点(0,-4),(0,4)a=5作业:书:习题8.1 1
优化设计
