指数函数及其性质
图片预览





文档简介
课件25张PPT。2.1.2《指数函数及其性质》
函数的定义.
复习回顾 函数的单调性、奇偶性的定义,及其判定方法.
复合函数单调性的判定方法. 本节重难点重点:(1)指数函数的概念和性质及其应用(2)指数函数底数a 对图象的影响(3)利用指数函数单调性熟练比较几个指数幂的大小难点:(1)利用函数单调性比较指数幂的大小(2)指数函数性质的归纳,概括及其应用
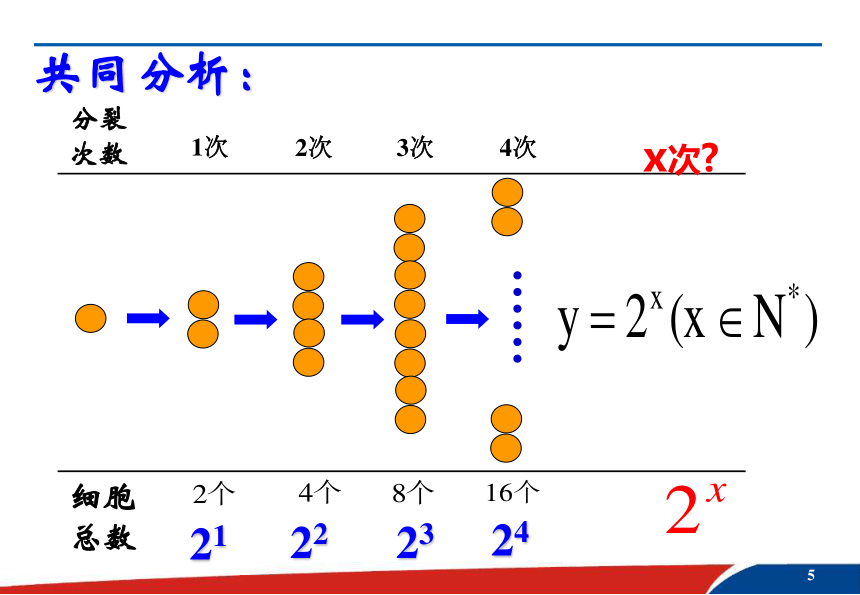
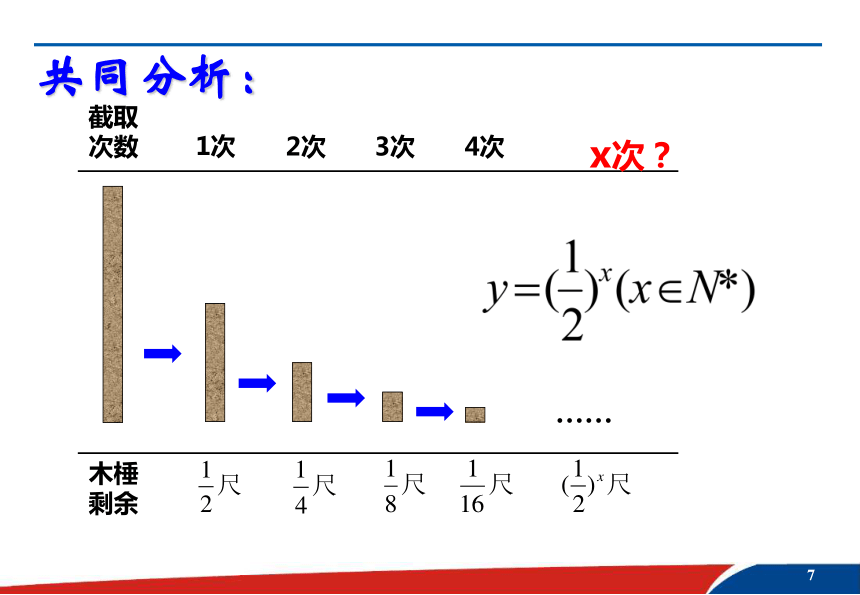
探索新知(一) 细胞分裂次数x与分裂后的细胞总数y的关系?21222324共同分析:探索新知(二) 《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。”请你写出截取x次之后,木棰剩余量y关于x的函数关系式?共同分析:……讨论1:以上两个函数有何共同特征?★归纳出指数函数定义:一起探讨: 思考?一、探究指数函数的定义1.2.1.考考你?下列函数中,哪些是指数函数? (√)(√) (√)(√)在同一直角坐标系画出 ,
讨论2:已知函数的解析式,怎么得到函数的图象呢? 一般采用什么方法?列表—描点—连线作图的图象.
和
并观察:两个函数的图象有什么关系?二、用描点法探究指数函数的图像和性质yx0 1 2 3 4 5 6 7 88
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3y = 2xy = x(0,1)y = 2xy = xy = 2xy = 3xy = 4x★指数函数的图像和性质:(0,1)a越来越大a越来越小指数函数在底数 及 ,这两种 情况下的图象和性质: (1)定义域:R (2)值域:(0,+∞)(3)过点(0,1)(4)在R上是减函数(4)在R上是增函数★归纳总结:1.求下列函数的定义域注意:应用指数函数的定义域 考考你?
小贴士 2. 已知指数函数 的图像经过点 求 的值.分析: 指数函数的图象经过点 ,有 ,
即 ,解得 ,于是有 ,所以:思考:确定一个指数函数需要什么条件?想一想3.试一试,你能比较下列每两个值的大小吗? ∵函数 在R上是增函数,
而指数2.5<3.(1)<解:(2) ∵函数 在R上是减函数,
而指数-0.1>-0.2解:∴<(3)根据指数函数的性质,得:且从而有>解:方法提炼:比较两个幂值大小的方法(1)构造指数函数并指明其单调性. (2)自变量的大小比较. (3)函数值的大小比较. 构造函数法: 数的特征是同底数不同指数. 2.寻求中间量: 当底数不同,指数也不同时. 大显身手:变式练习,比较下列各题中两个值的大小:有点难,我再想一想。1.指数函数的概念2.指数函数的图像和性质3.指数函数性质的简单应用 数形结合,由具体到一般★思想与方法:课堂小结2.1.2《指数函数及其性质》
函数的定义.
复习回顾 函数的单调性、奇偶性的定义,及其判定方法.
复合函数单调性的判定方法. 本节重难点重点:(1)指数函数的概念和性质及其应用(2)指数函数底数a 对图象的影响(3)利用指数函数单调性熟练比较几个指数幂的大小难点:(1)利用函数单调性比较指数幂的大小(2)指数函数性质的归纳,概括及其应用
探索新知(一) 细胞分裂次数x与分裂后的细胞总数y的关系?21222324共同分析:探索新知(二) 《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。”请你写出截取x次之后,木棰剩余量y关于x的函数关系式?共同分析:……讨论1:以上两个函数有何共同特征?★归纳出指数函数定义:一起探讨: 思考?一、探究指数函数的定义1.2.1.考考你?下列函数中,哪些是指数函数? (√)(√) (√)(√)在同一直角坐标系画出 ,
讨论2:已知函数的解析式,怎么得到函数的图象呢? 一般采用什么方法?列表—描点—连线作图的图象.
和
并观察:两个函数的图象有什么关系?二、用描点法探究指数函数的图像和性质yx0 1 2 3 4 5 6 7 88
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3y = 2xy = x(0,1)y = 2xy = xy = 2xy = 3xy = 4x★指数函数的图像和性质:(0,1)a越来越大a越来越小指数函数在底数 及 ,这两种 情况下的图象和性质: (1)定义域:R (2)值域:(0,+∞)(3)过点(0,1)(4)在R上是减函数(4)在R上是增函数★归纳总结:1.求下列函数的定义域注意:应用指数函数的定义域 考考你?
小贴士 2. 已知指数函数 的图像经过点 求 的值.分析: 指数函数的图象经过点 ,有 ,
即 ,解得 ,于是有 ,所以:思考:确定一个指数函数需要什么条件?想一想3.试一试,你能比较下列每两个值的大小吗? ∵函数 在R上是增函数,
而指数2.5<3.(1)<解:(2) ∵函数 在R上是减函数,
而指数-0.1>-0.2解:∴<(3)根据指数函数的性质,得:且从而有>解:方法提炼:比较两个幂值大小的方法(1)构造指数函数并指明其单调性. (2)自变量的大小比较. (3)函数值的大小比较. 构造函数法: 数的特征是同底数不同指数. 2.寻求中间量: 当底数不同,指数也不同时. 大显身手:变式练习,比较下列各题中两个值的大小:有点难,我再想一想。1.指数函数的概念2.指数函数的图像和性质3.指数函数性质的简单应用 数形结合,由具体到一般★思想与方法:课堂小结2.1.2《指数函数及其性质》
