(绝杀2013)高考物理 模拟+权威预测 专题四曲线运动
文档属性
| 名称 | (绝杀2013)高考物理 模拟+权威预测 专题四曲线运动 |  | |
| 格式 | zip | ||
| 文件大小 | 347.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2013-05-05 12:59:51 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
【绝杀2013】2013届高考物理模拟+权威预测:专题四曲线运动
【模拟演练】
1.(2012·洛阳模拟)小船横渡一条河,船头方向始终与河岸垂直.若小船相对水的速度大小不变时,小船的运动轨迹如图所示,则河水的流速( )
A.由A到B水速一直增大
B.由A到B水速一直减小
C.由A到B水速先增大后减小
D.由A到B水速先减小后增大
2.(2012·吉林模拟)固定在竖直平面的光滑圆弧轨道ABCD.其A点与圆心O等高,D点为轨道最高点,DB为竖直直线,AC为水平线,AE为水平面.今使小球自A点正上方某处由静止释放,从A点进入圆轨道,只要调节释放点的高度,总能使小球通过圆轨道的最高点D,则小球通过D点后( )
A.一定会落到水平面AE上
B.一定会再次落到圆轨道上
C.可能会落到水平面AE上,也可能会再次落到圆轨道上
D.以上说法都不正确
3.(2012·无锡模拟)如图所示的直角三角板紧贴在固定的刻度尺上方,现假使三角板沿刻度尺水平向右匀速运动的同时,一支铅笔从三角板直角边的最下端,由静止开始沿此边向上做匀加速直线运动,下列关于铅笔尖的运动及其留下的痕迹的判断中,正确的有( )
A.笔尖留下的痕迹是一条抛物线
B.笔尖留下的痕迹是一条倾斜的直线
C.在运动过程中,笔尖运动的速度方向始终保持不变
D.在运动过程中,笔尖运动的加速度方向始终保持不变
4.(2012·太原模拟)如图所示,一小物块在开口向上的半圆形曲面内以某一速率开始下滑,曲面内各处动摩擦因数不同,此摩擦作用使物块下滑时速率保持不变,则下列说法不正确的是( )
A.因物块速率保持不变,故加速度为零
B.物块受合外力大小不变,方向不断改变
C.在滑到最低点以前,物块对曲面的压力越来越大
D.在滑到最低点以前,物块受到的摩擦力越来越小
5.(2012·抚顺模拟)河水的流速与船离河岸的距离的变化关系如图乙所示,船在静水中的速度与时间的关系如图甲所示,则下列说法正确的是( )
A.船渡河的最短时间为60 s
B.要使船以最短时间渡河,船在行驶过程中,船头必须始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.船在河水中的最大速度是5 m/s
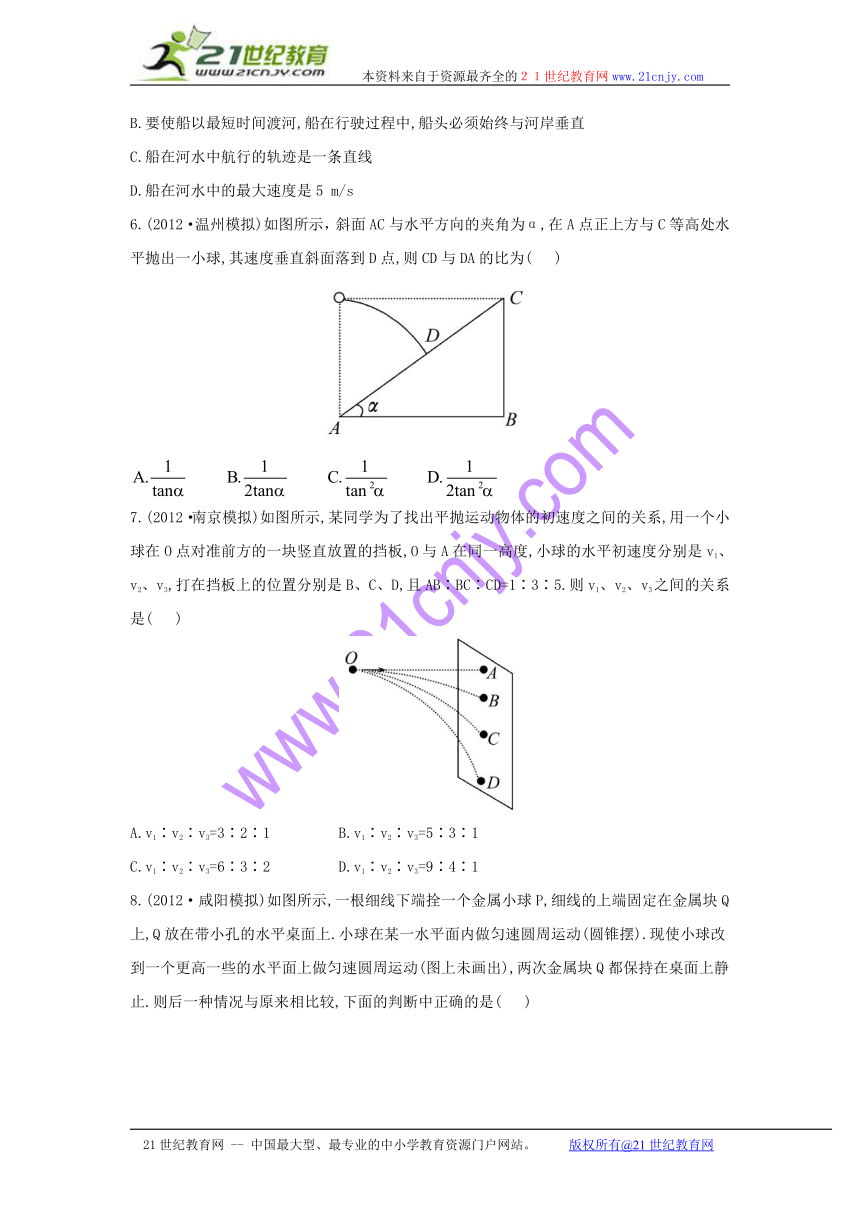
6.(2012·温州模拟)如图所示,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则CD与DA的比为( )
7.(2012·南京模拟)如图所示,某同学为了找出平抛运动物体的初速度之间的关系,用一个小球在O点对准前方的一块竖直放置的挡板,O与A在同一高度,小球的水平初速度分别是v1、v2、v3,打在挡板上的位置分别是B、C、D,且AB∶BC∶CD=1∶3∶5.则v1、v2、v3之间的关系是( )
A.v1∶v2∶v3=3∶2∶1 B.v1∶v2∶v3=5∶3∶1
C.v1∶v2∶v3=6∶3∶2 D.v1∶v2∶v3=9∶4∶1
8.(2012·咸阳模拟)如图所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔的水平桌面上.小球在某一水平面内做匀速圆周运动(圆锥摆).现使小球改到一个更高一些的水平面上做匀速圆周运动(图上未画出),两次金属块Q都保持在桌面上静止.则后一种情况与原来相比较,下面的判断中正确的是( )
A.Q受到桌面的支持力变大
B.Q受到桌面的静摩擦力变大
C.小球P运动的角速度变大
D.小球P运动的周期变大
9.(2011·厦门模拟)一快艇要从岸边某处到达河中离岸100 m远的浮标处,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,假设行驶中快艇在静水中航行的分速度方向选定后就不再改变,则( )
A.快艇的运动轨迹可能是直线
B.快艇的运动轨迹只能是曲线
C.最快到达浮标处通过的位移为100 m
D.最快到达浮标处所用时间为20 s
10.(2011·桂林模拟)如图所示,某游乐场有一水上转台,可在水平面内匀速转动,沿半径方向面对面手拉手坐着甲、乙两个小孩,假设两小孩的质量相等,他们与盘间的动摩擦因数相同,当圆盘转速加快到两小孩刚好还未发生滑动时,某一时刻两小孩突然松手,则两小孩的运动情况是( )
A.两小孩均沿切线方向滑出后落入水中
B.两小孩均沿半径方向滑出后落入水中
C.两小孩仍随圆盘一起做匀速圆周运动,不会发生滑动而落入水中
D.甲仍随圆盘一起做匀速圆周运动,乙发生滑动最终落入水中
11.(2011·镇江模拟)如图所示,A、B随水平圆盘绕轴匀速转动,物体B在水平方向所受的作用力有( )
A.圆盘对B及A对B的摩擦力,两力都指向圆心
B.圆盘对B的摩擦力指向圆心,A对B的摩擦力背离圆心
C.圆盘对B及A对B的摩擦力和向心力
D.圆盘对B的摩擦力和向心力
12.(2012·开封模拟)如图所示,长度为L的细绳上端固定在天花板上O点,下端拴着质量为m的小球.当把细绳拉直时,细绳与竖直线的夹角为θ=60°,小球恰与光滑水平面接触.
(1)当球以角速度ω1=做圆锥摆运动时,细绳的张力FT为多大 水平面受到的压力FN是多大
(2)当球以角速度ω2=做圆锥摆运动时,细绳的张力F′T及水平面受到的压力F′N各是多大
13.(2012·安庆模拟)如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0 m,BC段长L=1.5 m.弹射装置将一个小球(可视为质点)以v0=5 m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2 m,不计空气阻力,g取10 m/s2.求:
(1)小球在半圆轨道上运动时的角速度ω和加速度a的大小;
(2)小球从A点运动到C点的时间t′;
(3)桌子的高度h.
14.(2012·大连模拟)如图所示,在光滑水平面上竖直固定一半径为R的光滑半圆槽轨道,其底端恰与水平面相切.质量为m的小球以大小为v0的初速度经半圆槽轨道最低点B滚上半圆槽,小球恰能通过最高点C后落回到水平面上的A点.(不计空气阻力,重力加速度为g)求:
(1)小球通过B点时对半圆槽的压力大小;
(2)AB两点间的距离;
(3)小球落到A点时的速度方向
【高考预测】
曲线运动是高考的必考内容,主要呈现以下三点命题趋势:
(1)应用运动的合成与分解研究曲线运动.
(2)平抛运动规律、类平抛运动在生产生活及体育运动中的综合应用.
(3)圆周运动、牛顿第二定律、功能关系的综合考查.
对该部分内容的命题预测如下:
考查知识及角度 高考预测
相关联体速度的分解 1
圆周运动的运动学、动力学分析 2、3、6
平抛运动规律 4、5
圆周运动与能量的综合 7
1.如图所示,套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至与定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则( )
A.v2=v1 B.v2>v1 C.v2≠0 D.v2=0
2.在离地面足够高的光滑水平桌面上,沿着桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的小钢球接触,当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示,桌子的右边缘距墙壁的水平距离为s,让钢球向左压缩弹簧一段距离后静止释放,使钢球沿着水平方向射出桌面,小球在空中飞行后打在竖直墙壁上,下落高度为h,则( )
A.弹簧的压缩量x越大,其他条件不变,则下落高度越大
B.弹簧的压缩量x越大,其他条件不变,则下落高度越小
C.桌子右边缘距离墙壁的水平距离s越大,其他条件不变,则下落高度越大
D.桌子右边缘距离墙壁的水平距离s越大,其他条件不变,则下落高度越短
3.一内壁光滑的半径为R的圆筒固定,横截面在竖直平面内,圆筒内最低点有一小球.现给小球2.2mgR的初动能,使小球从最低点开始沿筒壁运动,则小球沿筒壁做圆周运动过程中( )
A.小球可以到达轨道的最高点
B.小球不能到达轨道的最高点
C.小球的最小速度大于
D.小球的最小速度等于
4.如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间恰好无作用力,则( )
A.该盒子做匀速圆周运动的周期一定小于
B.该盒子做匀速圆周运动的周期一定等于
C.盒子在最低点时盒子与小球之间的作用力大小可能小于2mg
D.盒子在最低点时盒子与小球之间的作用力大小可能大于2mg
5.如图所示,A、B、C三个小球分别从斜面的顶端以不同的速度水平抛出,其中A、B落到斜面上,C落到水平面上,A、B落到斜面上时速度方向与水平方向的夹角分别为α、β,C落到水平面上时速度方向与水平方向的夹角为γ,则( )
A.α=β=γ B.α=β>γ C.α=β<γ D.α<β<γ
6.一细绳穿过一光滑的、不动的细管,两端分别拴着质量为m和M的小球A、B.当小球A绕管子的中心轴转动时,A球摆开某一角度,此时A球到上管口的绳长为L,如图所示.细管的半径可以忽略.试求:
(1)小球A的速度和它所受的向心力;
(2)小球A转动的周期.
7.如图所示,AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的1/4圆周连接而成,它们的圆心O1、O2与两圆弧的连接点O在同一竖直线上.O2B沿水池的水面,O2和B两点位于同一水平面上.一个质量为m的小滑块可由弧AO的任意位置从静止开始滑下,不计一切摩擦.
(1)假设小滑块由A点静止下滑,求小滑块滑到O点时对O点的压力;
(2)凡能在O点脱离滑道的小滑块,其落水点到O2的距离在什么范围内;
(3)若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO上的何处(用该处到O1点的连线与竖直线的夹角的三角函数值表示).
答案解析
【模拟演练】
1.【解析】选B.小船的运动轨迹的切线方向为小船的速度方向,小船的速度与河水的速度方向的夹角越来越大,由题意知小船垂直河岸的速度不变,那么河水的流速越来越小,B正确.
2.【解题指南】解答本题应注意以下两点:
(1)小球能过最高点D的条件.
(2)小球从D抛出后,做平抛运动.
【解析】选A.小球通过最高点的临界条件是vD>,小球从D点飞出后做平抛运动,根据平抛运动的特点,当小球落到AE面上时,竖直方向上R=gt2,水平方向上x=vDt,故水平位移x>R,因此A项正确.
3.【解析】选A、D.由于笔尖在水平方向匀速运动,在竖直方向匀加速直线运动,故它们的合运动为匀变速曲线运动,属于类平抛运动,故A、D正确,B、C错误.
4.【解析】选A.物块速率不变,做匀速圆周运动,存在向心加速度,A错;做匀速圆周运动物块的向心力大小不变,方向指向圆心,B对;对物块受力分析如图,沿切线方向Ff=mgcosθ,随θ变大,Ff减小,D对.沿半径方向FN-mgsinθ=ma,即FN= ma+mgsinθ,随θ的增大FN增大,C对.
【误区警示】解答本题易产生的误区
(1)物块速率不变,认为速度不变,从而误认为A对.
(2)误认为μ不变,根据Ff=μFN,由于FN增大,从而认为Ff增大.
5.【解析】选B.河宽d=300 m,船在静水中的速度v=3 m/s,船渡河的最短时间t==100 s,选项A错;船头始终与河岸垂直时,渡河的时间最短,选项B正确;因河水的流速随船离河岸的距离的变化而变化,船航行的轨迹是一条曲线,选项C错;3 m/s 与4 m/s的合成最大值为7 m/s,即船在河水中的速度可以大于5 m/s,选项D错误.
6.【解析】选D.如图所示,设平抛初速度为v0,落到D处时的竖直速度为vy,所用时间为t,对Rt△AFD,AD=;对Rt△CED,CD=.在速度三角形中tanα=,解以上三式得,D对.
7.【解析】选C.根据平抛运动规律可知,小球在竖直方向上做自由落体运动,由于AB∶BC∶CD=1∶3∶5,则y1∶y2∶y3=1∶4∶9,又因为x=v0t,则y=,即v1∶v2∶v3==6∶3∶2,选项C正确.
8.【解析】选B、C.根据小球做圆周运动的特点,设绳与竖直方向的夹角为θ,故FT=,对物体Q受力分析,由平衡条件Ff=FTsinθ=mgtanθ,FN=FTcosθ+Mg=mg +Mg,故在θ增大时,Q受到的支持力不变,静摩擦力变大,A选项错误,B选项正确;由mgtanθ=mLsinθω2,得ω=,θ增大,故角速度变大,周期变小,故C选项正确,D选项错误.
9.【解析】选B、D.快艇的实际速度为快艇在静水中的速度与水速的合速度.由图象可知快艇在静水中为匀加速直线运动,水为匀速直线运动,两速度不能在一条直线上,故快艇必做曲线运动,B正确,A错误;当快艇与河岸垂直时,到达浮标处时间最短,而此时快艇做曲线运动,故位移大于100 m,C项错误;由题中甲图象可知快艇的加速度为a=,对快艇由x=at2得: =20 s,即最快到达浮标处所用时间为20 s,D项正确.
10.【解析】选D.在松手前,甲、乙两小孩做圆周运动的向心力均由静摩擦力及拉力的合力提供,且静摩擦力均达到了最大静摩擦力.因为这两个小孩在同一个圆盘上转动,故角速度ω相同,设此时手上的拉力为FT,则对甲:Ffm-FT=mω2R甲.对乙:FT+Ffm=mω2R乙,当松手时,FT=0,乙所受的最大静摩擦力小于所需要的向心力,故乙做离心运动,然后落入水中,甲所受的静摩擦力变小,直至与它所需要的向心力相等,故甲仍随圆盘一起做匀速圆周运动,选项D正确.
11.【解析】选B.A随B做匀速圆周运动,它所需的向心力由B对A的摩擦力来提供,因此B对A的摩擦力指向圆心,A对B的摩擦力背离圆心,圆盘对B的摩擦力指向圆心,才能使B受到指向圆心的合力,所以只有选项B正确.
12.【解析】设小球做圆锥摆运动的角速度为ω0时,小球对光滑水平面的压力恰好为零,此时球受重力mg和绳的拉力FT0,应用正交分解法列出方程:
FT0sinθ=mω02Lsinθ ①
FT0cosθ-mg=0 ②
由以上两式解得:ω0= ③
(1)因为ω1<ω0,所以小球受重力mg、绳的拉力FT和水平面的支持力FN,应用正交分解法列方程:
FTsinθ=mω12Lsinθ ④
FTcosθ+FN-mg=0 ⑤
解得:FT=mg,FN=
(2)因为ω2>ω0,小球离开水平面做圆锥摆运动,设细绳与竖直线的夹角为α,小球受重力mg和细绳的拉力F′T,应用正交分解法列方程:
F′Tsinα=mω22Lsinα ⑥
F′Tcosα-mg=0 ⑦
解得:cosα=,F′T=4mg,
由于球已离开水平面,所以球对水平面的压力F′N=0.
答案:(1)mg (2)4mg 0
13.【解析】(1)小球在圆轨道中的角速度
=5 rad/s
加速度
(2)小球从A到B的时间
从B到C的时间
小球从A到C的时间
t′=t1+t2=0.628 s+0.3 s=0.928 s
(3)由C到D,小球以初速度v0=5 m/s做平抛运动.由s=v0t,h=得
答案:(1)5 rad/s 25 m/s2 (2)0.928 s (3)0.8 m
14.【解析】(1)在B点小球开始做圆周运动,由牛顿第二定律得
FN-mg=
即:FN=mg+
(2)小球恰能通过C点,故只有重力提供向心力,
则mg=
过C点小球做平抛运动:sAB=vCt
h=gt2,h=2R
联立以上几式解得:sAB=2R
(3)设与水平方向成θ角,则tanθ=
v⊥=gt
2R=gt2
联立以上几式解得θ=arctan2
答案:(1)mg+ (2)2R
(3)与水平方向的夹角为arctan2
【高考预测】
1.【解析】选D.环上升过程其速度v1可分解为两个分速度v∥和v⊥,如图所示,
其中v∥为沿绳方向的速度,其大小等于重物B的速度v2;v⊥为绕定滑轮转动的线速度.关系式为v2=v1cosθ,θ为v1与v∥间的夹角.当A上升至与定滑轮的连线水平的位置时,θ=90°,cosθ=0,即此时v2=0,D正确.
【方法技巧】相关联体的速度分解方法
速度分解的基本原则是按实际运动效果分解,常见相关联体的分解法有:
方法一:先确定合速度的方向,即物体实际运动方向,然后分析这个合速度所产生的实际效果,以确定两个分速度的方向.
方法二:先假设合运动的一个位移,看看这个位移产生了什么效果,从中找到运动分解的方法.
2.【解析】选B、C.弹簧的压缩量越大,小球平抛的初速度越大,在s一定时,由s=v0t得t越小,故h=gt2越小,A错、B对.若s越大,v0一定时,t越大,故h越大,C对、D错.
3.【解析】选B、C.小球恰能达到最高点有mg=得v0=,假设小球能达到最高点,由机械能守恒定律可得Ek0=mv2+2mgR,则v=<v0,所以小球不能到达最高点,A选项错误,B选项正确;设当小球与圆心连线与水平方向夹角为θ时,小球与轨道恰好脱离,由牛顿第二定律可得mgsinθ=,由机械能守恒定律可得Ek0=mgR (1+sinθ)+mv′2,可得v′=,C选项正确,D选项错误.
4.【解析】选B.要使在最高点时盒子与小球之间恰好无作用力,则有mg=,解得该盒子做匀速圆周运动的速度v=,该盒子做匀速圆周运动的周期为T==.选项A错误,B正确;在最低点时,盒子与小球之间的作用力和小球重力的合力提供小球运动的向心力,由FN-mg=,解得FN=2mg,选项C、D错误.
5.【解析】选B.小球落到斜面上时,如图所示.
设斜面的倾角为θ,则tanα==2tanθ.由于θ为定值,故α=β;小球落到平面上时,如图所示.若忽略平面,将斜面延长,γ继续增大才能与α相等,故α=β>γ,B对.
【方法技巧】平抛运动的解题技巧
(1)突出落点位置问题一般要建立水平位移和竖直位移之间的关系.
(2)突出落点方向即末速度的方向的问题,一般要建立水平速度和竖直速度之间的关系.
(3)注意挖掘和利用合运动、分运动及题设情境之间的几何关系.
6.【解析】(1)设绳子的拉力为T,绳子与竖直方向的夹角为θ,
对于小球A,由牛顿第二定律得:
竖直方向:Tcosθ=mg ①
水平方向:Tsinθ=mω2Lsinθ ②
对于小球B有:T=Mg ③
联立各式解得:ω=
则小球A的速度为:v=ωLsinθ=sinθ
小球A所受的向心力就是张力T在水平方向的分力,即:F=Tsinθ=Mgsinθ
由①③得:cosθ=
故sinθ=,所以
F=Mgsinθ=Mg
(2)小球A转动的周期为:
T=
答案:(1) Mg (2)
7.【解析】(1)mgR=mv2,FN-mg=mv2/R,联立得:FN=3mg
由牛顿第三定律得:压力大小为3mg,方向竖直向下.
(2)从A点下滑的滑块到O点的速度为,即最大速度v2=,设能脱离轨道的最小速度为v1
则有:mg=,
得:v1=
由R=gt2,x=vt,
解得xmin=R,xmax=2R
所以所求距离:R≤x≤2R
(3)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是
由机械能守恒
2mgR(1-cosθ)=mv2
联立解得cosθ=
答案:(1)3mg,方向竖直向下 (2)R≤x≤2R (3)见解析
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
【绝杀2013】2013届高考物理模拟+权威预测:专题四曲线运动
【模拟演练】
1.(2012·洛阳模拟)小船横渡一条河,船头方向始终与河岸垂直.若小船相对水的速度大小不变时,小船的运动轨迹如图所示,则河水的流速( )
A.由A到B水速一直增大
B.由A到B水速一直减小
C.由A到B水速先增大后减小
D.由A到B水速先减小后增大
2.(2012·吉林模拟)固定在竖直平面的光滑圆弧轨道ABCD.其A点与圆心O等高,D点为轨道最高点,DB为竖直直线,AC为水平线,AE为水平面.今使小球自A点正上方某处由静止释放,从A点进入圆轨道,只要调节释放点的高度,总能使小球通过圆轨道的最高点D,则小球通过D点后( )
A.一定会落到水平面AE上
B.一定会再次落到圆轨道上
C.可能会落到水平面AE上,也可能会再次落到圆轨道上
D.以上说法都不正确
3.(2012·无锡模拟)如图所示的直角三角板紧贴在固定的刻度尺上方,现假使三角板沿刻度尺水平向右匀速运动的同时,一支铅笔从三角板直角边的最下端,由静止开始沿此边向上做匀加速直线运动,下列关于铅笔尖的运动及其留下的痕迹的判断中,正确的有( )
A.笔尖留下的痕迹是一条抛物线
B.笔尖留下的痕迹是一条倾斜的直线
C.在运动过程中,笔尖运动的速度方向始终保持不变
D.在运动过程中,笔尖运动的加速度方向始终保持不变
4.(2012·太原模拟)如图所示,一小物块在开口向上的半圆形曲面内以某一速率开始下滑,曲面内各处动摩擦因数不同,此摩擦作用使物块下滑时速率保持不变,则下列说法不正确的是( )
A.因物块速率保持不变,故加速度为零
B.物块受合外力大小不变,方向不断改变
C.在滑到最低点以前,物块对曲面的压力越来越大
D.在滑到最低点以前,物块受到的摩擦力越来越小
5.(2012·抚顺模拟)河水的流速与船离河岸的距离的变化关系如图乙所示,船在静水中的速度与时间的关系如图甲所示,则下列说法正确的是( )
A.船渡河的最短时间为60 s
B.要使船以最短时间渡河,船在行驶过程中,船头必须始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.船在河水中的最大速度是5 m/s
6.(2012·温州模拟)如图所示,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则CD与DA的比为( )
7.(2012·南京模拟)如图所示,某同学为了找出平抛运动物体的初速度之间的关系,用一个小球在O点对准前方的一块竖直放置的挡板,O与A在同一高度,小球的水平初速度分别是v1、v2、v3,打在挡板上的位置分别是B、C、D,且AB∶BC∶CD=1∶3∶5.则v1、v2、v3之间的关系是( )
A.v1∶v2∶v3=3∶2∶1 B.v1∶v2∶v3=5∶3∶1
C.v1∶v2∶v3=6∶3∶2 D.v1∶v2∶v3=9∶4∶1
8.(2012·咸阳模拟)如图所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔的水平桌面上.小球在某一水平面内做匀速圆周运动(圆锥摆).现使小球改到一个更高一些的水平面上做匀速圆周运动(图上未画出),两次金属块Q都保持在桌面上静止.则后一种情况与原来相比较,下面的判断中正确的是( )
A.Q受到桌面的支持力变大
B.Q受到桌面的静摩擦力变大
C.小球P运动的角速度变大
D.小球P运动的周期变大
9.(2011·厦门模拟)一快艇要从岸边某处到达河中离岸100 m远的浮标处,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,假设行驶中快艇在静水中航行的分速度方向选定后就不再改变,则( )
A.快艇的运动轨迹可能是直线
B.快艇的运动轨迹只能是曲线
C.最快到达浮标处通过的位移为100 m
D.最快到达浮标处所用时间为20 s
10.(2011·桂林模拟)如图所示,某游乐场有一水上转台,可在水平面内匀速转动,沿半径方向面对面手拉手坐着甲、乙两个小孩,假设两小孩的质量相等,他们与盘间的动摩擦因数相同,当圆盘转速加快到两小孩刚好还未发生滑动时,某一时刻两小孩突然松手,则两小孩的运动情况是( )
A.两小孩均沿切线方向滑出后落入水中
B.两小孩均沿半径方向滑出后落入水中
C.两小孩仍随圆盘一起做匀速圆周运动,不会发生滑动而落入水中
D.甲仍随圆盘一起做匀速圆周运动,乙发生滑动最终落入水中
11.(2011·镇江模拟)如图所示,A、B随水平圆盘绕轴匀速转动,物体B在水平方向所受的作用力有( )
A.圆盘对B及A对B的摩擦力,两力都指向圆心
B.圆盘对B的摩擦力指向圆心,A对B的摩擦力背离圆心
C.圆盘对B及A对B的摩擦力和向心力
D.圆盘对B的摩擦力和向心力
12.(2012·开封模拟)如图所示,长度为L的细绳上端固定在天花板上O点,下端拴着质量为m的小球.当把细绳拉直时,细绳与竖直线的夹角为θ=60°,小球恰与光滑水平面接触.
(1)当球以角速度ω1=做圆锥摆运动时,细绳的张力FT为多大 水平面受到的压力FN是多大
(2)当球以角速度ω2=做圆锥摆运动时,细绳的张力F′T及水平面受到的压力F′N各是多大
13.(2012·安庆模拟)如图所示,用内壁光滑的薄壁细圆管弯成的由半圆形APB(圆半径比细管的内径大得多)和直线BC组成的轨道固定在水平桌面上,已知APB部分的半径R=1.0 m,BC段长L=1.5 m.弹射装置将一个小球(可视为质点)以v0=5 m/s的水平初速度从A点弹入轨道,小球从C点离开轨道随即水平抛出,落地点D离开C的水平距离s=2 m,不计空气阻力,g取10 m/s2.求:
(1)小球在半圆轨道上运动时的角速度ω和加速度a的大小;
(2)小球从A点运动到C点的时间t′;
(3)桌子的高度h.
14.(2012·大连模拟)如图所示,在光滑水平面上竖直固定一半径为R的光滑半圆槽轨道,其底端恰与水平面相切.质量为m的小球以大小为v0的初速度经半圆槽轨道最低点B滚上半圆槽,小球恰能通过最高点C后落回到水平面上的A点.(不计空气阻力,重力加速度为g)求:
(1)小球通过B点时对半圆槽的压力大小;
(2)AB两点间的距离;
(3)小球落到A点时的速度方向
【高考预测】
曲线运动是高考的必考内容,主要呈现以下三点命题趋势:
(1)应用运动的合成与分解研究曲线运动.
(2)平抛运动规律、类平抛运动在生产生活及体育运动中的综合应用.
(3)圆周运动、牛顿第二定律、功能关系的综合考查.
对该部分内容的命题预测如下:
考查知识及角度 高考预测
相关联体速度的分解 1
圆周运动的运动学、动力学分析 2、3、6
平抛运动规律 4、5
圆周运动与能量的综合 7
1.如图所示,套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至与定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则( )
A.v2=v1 B.v2>v1 C.v2≠0 D.v2=0
2.在离地面足够高的光滑水平桌面上,沿着桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的小钢球接触,当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图所示,桌子的右边缘距墙壁的水平距离为s,让钢球向左压缩弹簧一段距离后静止释放,使钢球沿着水平方向射出桌面,小球在空中飞行后打在竖直墙壁上,下落高度为h,则( )
A.弹簧的压缩量x越大,其他条件不变,则下落高度越大
B.弹簧的压缩量x越大,其他条件不变,则下落高度越小
C.桌子右边缘距离墙壁的水平距离s越大,其他条件不变,则下落高度越大
D.桌子右边缘距离墙壁的水平距离s越大,其他条件不变,则下落高度越短
3.一内壁光滑的半径为R的圆筒固定,横截面在竖直平面内,圆筒内最低点有一小球.现给小球2.2mgR的初动能,使小球从最低点开始沿筒壁运动,则小球沿筒壁做圆周运动过程中( )
A.小球可以到达轨道的最高点
B.小球不能到达轨道的最高点
C.小球的最小速度大于
D.小球的最小速度等于
4.如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间恰好无作用力,则( )
A.该盒子做匀速圆周运动的周期一定小于
B.该盒子做匀速圆周运动的周期一定等于
C.盒子在最低点时盒子与小球之间的作用力大小可能小于2mg
D.盒子在最低点时盒子与小球之间的作用力大小可能大于2mg
5.如图所示,A、B、C三个小球分别从斜面的顶端以不同的速度水平抛出,其中A、B落到斜面上,C落到水平面上,A、B落到斜面上时速度方向与水平方向的夹角分别为α、β,C落到水平面上时速度方向与水平方向的夹角为γ,则( )
A.α=β=γ B.α=β>γ C.α=β<γ D.α<β<γ
6.一细绳穿过一光滑的、不动的细管,两端分别拴着质量为m和M的小球A、B.当小球A绕管子的中心轴转动时,A球摆开某一角度,此时A球到上管口的绳长为L,如图所示.细管的半径可以忽略.试求:
(1)小球A的速度和它所受的向心力;
(2)小球A转动的周期.
7.如图所示,AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的1/4圆周连接而成,它们的圆心O1、O2与两圆弧的连接点O在同一竖直线上.O2B沿水池的水面,O2和B两点位于同一水平面上.一个质量为m的小滑块可由弧AO的任意位置从静止开始滑下,不计一切摩擦.
(1)假设小滑块由A点静止下滑,求小滑块滑到O点时对O点的压力;
(2)凡能在O点脱离滑道的小滑块,其落水点到O2的距离在什么范围内;
(3)若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO上的何处(用该处到O1点的连线与竖直线的夹角的三角函数值表示).
答案解析
【模拟演练】
1.【解析】选B.小船的运动轨迹的切线方向为小船的速度方向,小船的速度与河水的速度方向的夹角越来越大,由题意知小船垂直河岸的速度不变,那么河水的流速越来越小,B正确.
2.【解题指南】解答本题应注意以下两点:
(1)小球能过最高点D的条件.
(2)小球从D抛出后,做平抛运动.
【解析】选A.小球通过最高点的临界条件是vD>,小球从D点飞出后做平抛运动,根据平抛运动的特点,当小球落到AE面上时,竖直方向上R=gt2,水平方向上x=vDt,故水平位移x>R,因此A项正确.
3.【解析】选A、D.由于笔尖在水平方向匀速运动,在竖直方向匀加速直线运动,故它们的合运动为匀变速曲线运动,属于类平抛运动,故A、D正确,B、C错误.
4.【解析】选A.物块速率不变,做匀速圆周运动,存在向心加速度,A错;做匀速圆周运动物块的向心力大小不变,方向指向圆心,B对;对物块受力分析如图,沿切线方向Ff=mgcosθ,随θ变大,Ff减小,D对.沿半径方向FN-mgsinθ=ma,即FN= ma+mgsinθ,随θ的增大FN增大,C对.
【误区警示】解答本题易产生的误区
(1)物块速率不变,认为速度不变,从而误认为A对.
(2)误认为μ不变,根据Ff=μFN,由于FN增大,从而认为Ff增大.
5.【解析】选B.河宽d=300 m,船在静水中的速度v=3 m/s,船渡河的最短时间t==100 s,选项A错;船头始终与河岸垂直时,渡河的时间最短,选项B正确;因河水的流速随船离河岸的距离的变化而变化,船航行的轨迹是一条曲线,选项C错;3 m/s 与4 m/s的合成最大值为7 m/s,即船在河水中的速度可以大于5 m/s,选项D错误.
6.【解析】选D.如图所示,设平抛初速度为v0,落到D处时的竖直速度为vy,所用时间为t,对Rt△AFD,AD=;对Rt△CED,CD=.在速度三角形中tanα=,解以上三式得,D对.
7.【解析】选C.根据平抛运动规律可知,小球在竖直方向上做自由落体运动,由于AB∶BC∶CD=1∶3∶5,则y1∶y2∶y3=1∶4∶9,又因为x=v0t,则y=,即v1∶v2∶v3==6∶3∶2,选项C正确.
8.【解析】选B、C.根据小球做圆周运动的特点,设绳与竖直方向的夹角为θ,故FT=,对物体Q受力分析,由平衡条件Ff=FTsinθ=mgtanθ,FN=FTcosθ+Mg=mg +Mg,故在θ增大时,Q受到的支持力不变,静摩擦力变大,A选项错误,B选项正确;由mgtanθ=mLsinθω2,得ω=,θ增大,故角速度变大,周期变小,故C选项正确,D选项错误.
9.【解析】选B、D.快艇的实际速度为快艇在静水中的速度与水速的合速度.由图象可知快艇在静水中为匀加速直线运动,水为匀速直线运动,两速度不能在一条直线上,故快艇必做曲线运动,B正确,A错误;当快艇与河岸垂直时,到达浮标处时间最短,而此时快艇做曲线运动,故位移大于100 m,C项错误;由题中甲图象可知快艇的加速度为a=,对快艇由x=at2得: =20 s,即最快到达浮标处所用时间为20 s,D项正确.
10.【解析】选D.在松手前,甲、乙两小孩做圆周运动的向心力均由静摩擦力及拉力的合力提供,且静摩擦力均达到了最大静摩擦力.因为这两个小孩在同一个圆盘上转动,故角速度ω相同,设此时手上的拉力为FT,则对甲:Ffm-FT=mω2R甲.对乙:FT+Ffm=mω2R乙,当松手时,FT=0,乙所受的最大静摩擦力小于所需要的向心力,故乙做离心运动,然后落入水中,甲所受的静摩擦力变小,直至与它所需要的向心力相等,故甲仍随圆盘一起做匀速圆周运动,选项D正确.
11.【解析】选B.A随B做匀速圆周运动,它所需的向心力由B对A的摩擦力来提供,因此B对A的摩擦力指向圆心,A对B的摩擦力背离圆心,圆盘对B的摩擦力指向圆心,才能使B受到指向圆心的合力,所以只有选项B正确.
12.【解析】设小球做圆锥摆运动的角速度为ω0时,小球对光滑水平面的压力恰好为零,此时球受重力mg和绳的拉力FT0,应用正交分解法列出方程:
FT0sinθ=mω02Lsinθ ①
FT0cosθ-mg=0 ②
由以上两式解得:ω0= ③
(1)因为ω1<ω0,所以小球受重力mg、绳的拉力FT和水平面的支持力FN,应用正交分解法列方程:
FTsinθ=mω12Lsinθ ④
FTcosθ+FN-mg=0 ⑤
解得:FT=mg,FN=
(2)因为ω2>ω0,小球离开水平面做圆锥摆运动,设细绳与竖直线的夹角为α,小球受重力mg和细绳的拉力F′T,应用正交分解法列方程:
F′Tsinα=mω22Lsinα ⑥
F′Tcosα-mg=0 ⑦
解得:cosα=,F′T=4mg,
由于球已离开水平面,所以球对水平面的压力F′N=0.
答案:(1)mg (2)4mg 0
13.【解析】(1)小球在圆轨道中的角速度
=5 rad/s
加速度
(2)小球从A到B的时间
从B到C的时间
小球从A到C的时间
t′=t1+t2=0.628 s+0.3 s=0.928 s
(3)由C到D,小球以初速度v0=5 m/s做平抛运动.由s=v0t,h=得
答案:(1)5 rad/s 25 m/s2 (2)0.928 s (3)0.8 m
14.【解析】(1)在B点小球开始做圆周运动,由牛顿第二定律得
FN-mg=
即:FN=mg+
(2)小球恰能通过C点,故只有重力提供向心力,
则mg=
过C点小球做平抛运动:sAB=vCt
h=gt2,h=2R
联立以上几式解得:sAB=2R
(3)设与水平方向成θ角,则tanθ=
v⊥=gt
2R=gt2
联立以上几式解得θ=arctan2
答案:(1)mg+ (2)2R
(3)与水平方向的夹角为arctan2
【高考预测】
1.【解析】选D.环上升过程其速度v1可分解为两个分速度v∥和v⊥,如图所示,
其中v∥为沿绳方向的速度,其大小等于重物B的速度v2;v⊥为绕定滑轮转动的线速度.关系式为v2=v1cosθ,θ为v1与v∥间的夹角.当A上升至与定滑轮的连线水平的位置时,θ=90°,cosθ=0,即此时v2=0,D正确.
【方法技巧】相关联体的速度分解方法
速度分解的基本原则是按实际运动效果分解,常见相关联体的分解法有:
方法一:先确定合速度的方向,即物体实际运动方向,然后分析这个合速度所产生的实际效果,以确定两个分速度的方向.
方法二:先假设合运动的一个位移,看看这个位移产生了什么效果,从中找到运动分解的方法.
2.【解析】选B、C.弹簧的压缩量越大,小球平抛的初速度越大,在s一定时,由s=v0t得t越小,故h=gt2越小,A错、B对.若s越大,v0一定时,t越大,故h越大,C对、D错.
3.【解析】选B、C.小球恰能达到最高点有mg=得v0=,假设小球能达到最高点,由机械能守恒定律可得Ek0=mv2+2mgR,则v=<v0,所以小球不能到达最高点,A选项错误,B选项正确;设当小球与圆心连线与水平方向夹角为θ时,小球与轨道恰好脱离,由牛顿第二定律可得mgsinθ=,由机械能守恒定律可得Ek0=mgR (1+sinθ)+mv′2,可得v′=,C选项正确,D选项错误.
4.【解析】选B.要使在最高点时盒子与小球之间恰好无作用力,则有mg=,解得该盒子做匀速圆周运动的速度v=,该盒子做匀速圆周运动的周期为T==.选项A错误,B正确;在最低点时,盒子与小球之间的作用力和小球重力的合力提供小球运动的向心力,由FN-mg=,解得FN=2mg,选项C、D错误.
5.【解析】选B.小球落到斜面上时,如图所示.
设斜面的倾角为θ,则tanα==2tanθ.由于θ为定值,故α=β;小球落到平面上时,如图所示.若忽略平面,将斜面延长,γ继续增大才能与α相等,故α=β>γ,B对.
【方法技巧】平抛运动的解题技巧
(1)突出落点位置问题一般要建立水平位移和竖直位移之间的关系.
(2)突出落点方向即末速度的方向的问题,一般要建立水平速度和竖直速度之间的关系.
(3)注意挖掘和利用合运动、分运动及题设情境之间的几何关系.
6.【解析】(1)设绳子的拉力为T,绳子与竖直方向的夹角为θ,
对于小球A,由牛顿第二定律得:
竖直方向:Tcosθ=mg ①
水平方向:Tsinθ=mω2Lsinθ ②
对于小球B有:T=Mg ③
联立各式解得:ω=
则小球A的速度为:v=ωLsinθ=sinθ
小球A所受的向心力就是张力T在水平方向的分力,即:F=Tsinθ=Mgsinθ
由①③得:cosθ=
故sinθ=,所以
F=Mgsinθ=Mg
(2)小球A转动的周期为:
T=
答案:(1) Mg (2)
7.【解析】(1)mgR=mv2,FN-mg=mv2/R,联立得:FN=3mg
由牛顿第三定律得:压力大小为3mg,方向竖直向下.
(2)从A点下滑的滑块到O点的速度为,即最大速度v2=,设能脱离轨道的最小速度为v1
则有:mg=,
得:v1=
由R=gt2,x=vt,
解得xmin=R,xmax=2R
所以所求距离:R≤x≤2R
(3)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是
由机械能守恒
2mgR(1-cosθ)=mv2
联立解得cosθ=
答案:(1)3mg,方向竖直向下 (2)R≤x≤2R (3)见解析
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
