2020-2021学年人教版八年级下册数学第18章《平行四边形》(3)(含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》(3)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 782.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 15:43:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在 中, ,则 等于( )
A. B. C. D.
2.下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形.
B.有一组邻边相等的平行四边形是菱形.
C.对角线相互垂直且相等的四边形是菱形.
D.有一组对边平行且相等的四边形是菱形.
3.如图,正方形ABCD的边长为7,在各边上顺次截取,则四边形EFGH的面积为( ).
A.20 B.25 C.30 D.35
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,点为矩形的对称中心,点从点出发沿向点运动到点停止,延长交于点,则四边形形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形 B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形-菱形→矩形 D.正方形→菱形→平行四边形→矩形
6.如图,已知,长方形的顶点,在两边上运动,若,,则线段的最大值为( )
A. B. C.4 D.
7.如图,四边形是平行四边形,将延长至点,若,则等于( )
A.110° B.35° C.80° D.55°
8.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A..2 B.3 C. D.
9.如图,四边形是边长为9的正方形纸片,将其沿折叠,使点落在边上的处,点的对应点为,且,则的长是( )
A.1 B.1.5 C.2 D.2.5
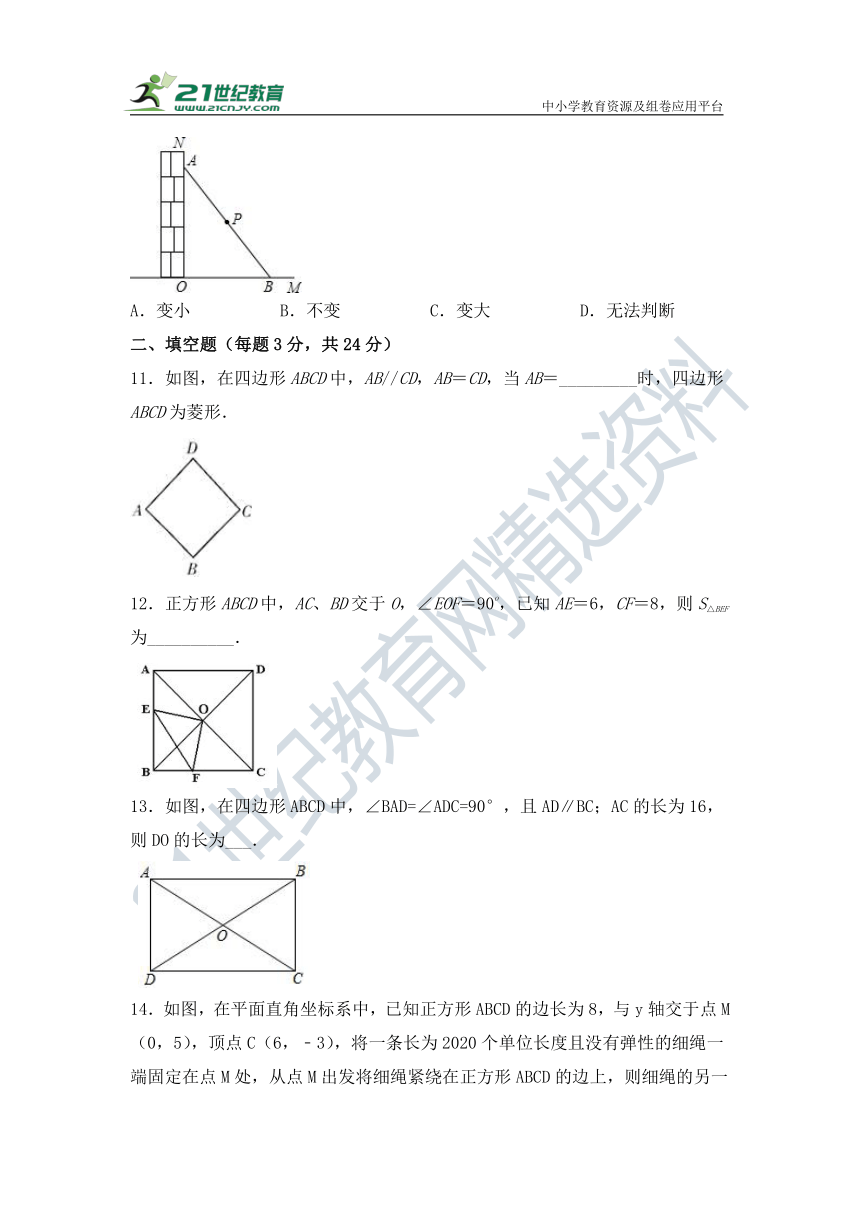
10.如图,一根木棍斜靠在与地面垂直的墙上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小 B.不变 C.变大 D.无法判断
二、填空题(每题3分,共24分)
11.如图,在四边形ABCD中,AB//CD,AB=CD,当AB=_________时,四边形ABCD为菱形.
12.正方形ABCD中,AC、BD交于O,∠EOF=90o,已知AE=6,CF=8,则S△BEF为__________.
13.如图,在四边形ABCD中,∠BAD=∠ADC=90°,且AD∥BC;AC的长为16,则DO的长为___.
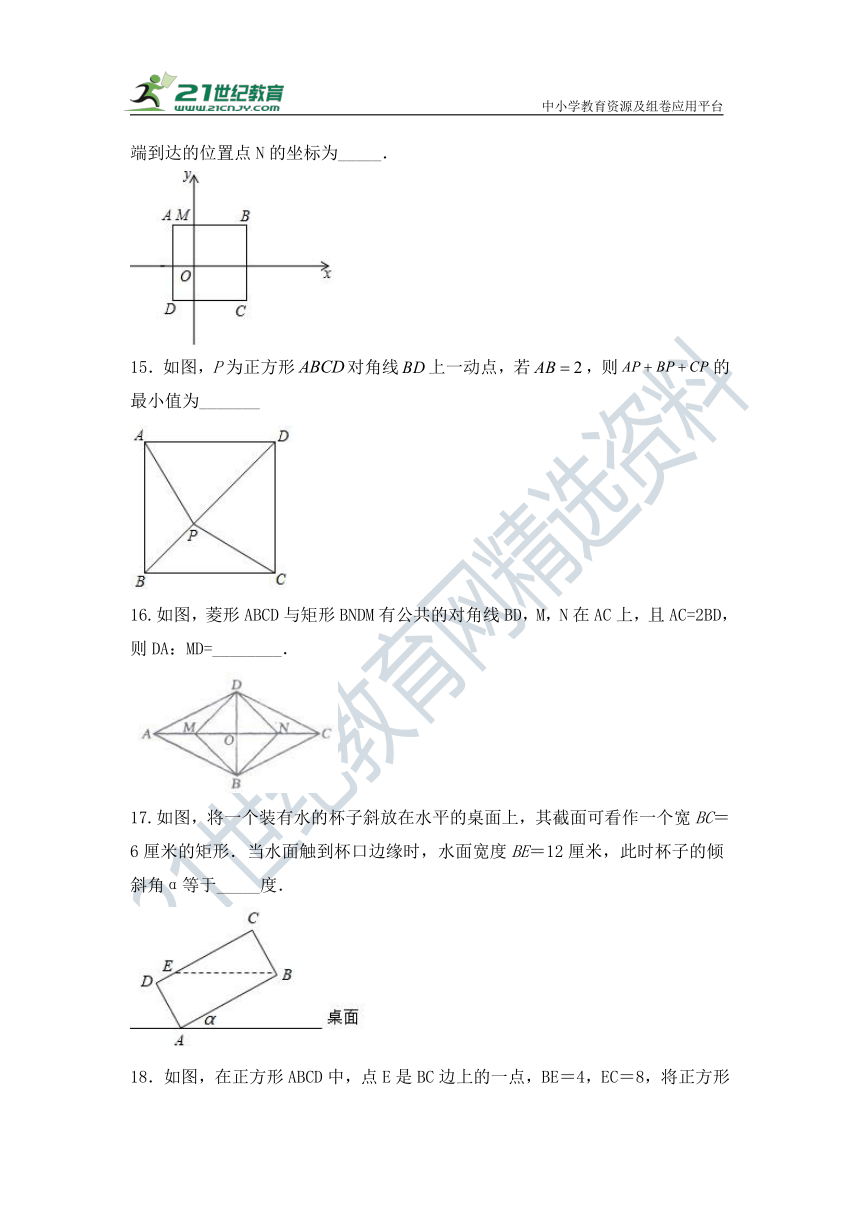
14.如图,在平面直角坐标系中,已知正方形ABCD的边长为8,与y轴交于点M(0,5),顶点C(6,﹣3),将一条长为2020个单位长度且没有弹性的细绳一端固定在点M处,从点M出发将细绳紧绕在正方形ABCD的边上,则细绳的另一端到达的位置点N的坐标为_____.
15.如图,P为正方形对角线上一动点,若,则的最小值为_______
16.如图,菱形ABCD与矩形BNDM有公共的对角线BD,M,N在AC上,且AC=2BD,则DA:MD=________.
17.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC=6厘米的矩形.当水面触到杯口边缘时,水面宽度BE=12厘米,此时杯子的倾斜角α等于_____度.
18.如图,在正方形ABCD中,点E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于点G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③;④S△GFC=14.4.其中结论正确的序号是________.
三、解答题(本题共有6小题,共46分,19题6分,20—24题8分)
19.(6分)如图,平行四边形的对角线交于点,若,,,求的长
20.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
21.如图,在平行四边形中,对角线与相交于点,点在对角线上,且,求证:
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明:四边形ADCF是菱形;
(2)若AC=4,AB=5,求出菱形ADCF的面积.
24.(8分)如图① ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.
参考答案
1.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D B A C B C B
二.填空题
11.BC(答案不唯一)
12.24
13.8
14.(﹣2,3)或(4,5)
15.
16.
17.30.
18.①③④
三、解答题
19.解:∵四边形ABCD是平行四边形,,,
∴,,AB=CD;
∵,
∴,
∴∠BCA=90°,
∴,
∴.
20.证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
21.解:∵四边形是平行四边形
∴,
又∵
∴
∴
在和中
∴
∴
∴
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23. (1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
∴AF=DB,
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴ ,
∴平行四边形ADCF是菱形
(2)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC= AB AC= ×5×4=10
24.(1)证明如下;(2)①当为时,;②的周长为.
(1)∵四边形ABCD 是平行四边形
∴
∴
在和中,
∴
∴;
(2)①∵四边形ABCD 是平行四边形,
∴
又
∴
是等腰直角三角形
若,则
∴
故当为时,;
②∵四边形ABCD 是平行四边形
又∵
∴EF垂直平分AC
∴
由①知,,即
则的周长为
故的周长为.
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在 中, ,则 等于( )
A. B. C. D.
2.下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形.
B.有一组邻边相等的平行四边形是菱形.
C.对角线相互垂直且相等的四边形是菱形.
D.有一组对边平行且相等的四边形是菱形.
3.如图,正方形ABCD的边长为7,在各边上顺次截取,则四边形EFGH的面积为( ).
A.20 B.25 C.30 D.35
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,点为矩形的对称中心,点从点出发沿向点运动到点停止,延长交于点,则四边形形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形 B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形-菱形→矩形 D.正方形→菱形→平行四边形→矩形
6.如图,已知,长方形的顶点,在两边上运动,若,,则线段的最大值为( )
A. B. C.4 D.
7.如图,四边形是平行四边形,将延长至点,若,则等于( )
A.110° B.35° C.80° D.55°
8.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A..2 B.3 C. D.
9.如图,四边形是边长为9的正方形纸片,将其沿折叠,使点落在边上的处,点的对应点为,且,则的长是( )
A.1 B.1.5 C.2 D.2.5
10.如图,一根木棍斜靠在与地面垂直的墙上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小 B.不变 C.变大 D.无法判断
二、填空题(每题3分,共24分)
11.如图,在四边形ABCD中,AB//CD,AB=CD,当AB=_________时,四边形ABCD为菱形.
12.正方形ABCD中,AC、BD交于O,∠EOF=90o,已知AE=6,CF=8,则S△BEF为__________.
13.如图,在四边形ABCD中,∠BAD=∠ADC=90°,且AD∥BC;AC的长为16,则DO的长为___.
14.如图,在平面直角坐标系中,已知正方形ABCD的边长为8,与y轴交于点M(0,5),顶点C(6,﹣3),将一条长为2020个单位长度且没有弹性的细绳一端固定在点M处,从点M出发将细绳紧绕在正方形ABCD的边上,则细绳的另一端到达的位置点N的坐标为_____.
15.如图,P为正方形对角线上一动点,若,则的最小值为_______
16.如图,菱形ABCD与矩形BNDM有公共的对角线BD,M,N在AC上,且AC=2BD,则DA:MD=________.
17.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC=6厘米的矩形.当水面触到杯口边缘时,水面宽度BE=12厘米,此时杯子的倾斜角α等于_____度.
18.如图,在正方形ABCD中,点E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于点G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③;④S△GFC=14.4.其中结论正确的序号是________.
三、解答题(本题共有6小题,共46分,19题6分,20—24题8分)
19.(6分)如图,平行四边形的对角线交于点,若,,,求的长
20.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
21.如图,在平行四边形中,对角线与相交于点,点在对角线上,且,求证:
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明:四边形ADCF是菱形;
(2)若AC=4,AB=5,求出菱形ADCF的面积.
24.(8分)如图① ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.
参考答案
1.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D B A C B C B
二.填空题
11.BC(答案不唯一)
12.24
13.8
14.(﹣2,3)或(4,5)
15.
16.
17.30.
18.①③④
三、解答题
19.解:∵四边形ABCD是平行四边形,,,
∴,,AB=CD;
∵,
∴,
∴∠BCA=90°,
∴,
∴.
20.证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
21.解:∵四边形是平行四边形
∴,
又∵
∴
∴
在和中
∴
∴
∴
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23. (1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
∴AF=DB,
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴ ,
∴平行四边形ADCF是菱形
(2)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC= AB AC= ×5×4=10
24.(1)证明如下;(2)①当为时,;②的周长为.
(1)∵四边形ABCD 是平行四边形
∴
∴
在和中,
∴
∴;
(2)①∵四边形ABCD 是平行四边形,
∴
又
∴
是等腰直角三角形
若,则
∴
故当为时,;
②∵四边形ABCD 是平行四边形
又∵
∴EF垂直平分AC
∴
由①知,,即
则的周长为
故的周长为.
