【慧学智评】北师大版九上数学 1-8 正方形的判定 同步授课课件
文档属性
| 名称 | 【慧学智评】北师大版九上数学 1-8 正方形的判定 同步授课课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第一章
特殊的平行四边形
第8课
长方形的判定
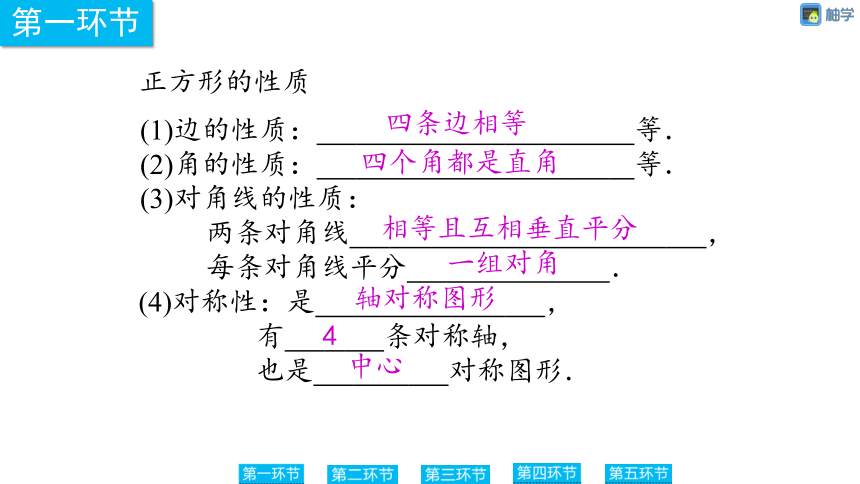
(1)边的性质:%// //% 等.
(2)角的性质:%// //% 等.
(3)对角线的性质:
两条对角线%// //%,
每条对角线平分%// //%.
(4)对称性:是%// //%,
有%// //%条对称轴,
也是%// //%对称图形.
四条边相等
四个角都是直角
相等且互相垂直平分
一组对角
轴对称图形
4
中心
正方形的性质
【问题1】正方形的定义:有一组邻边 ,
并且有一个角是 的平行四边形是正方形.
相等
直角
【问题2】要证明一个四边形是正方形,就是要证明这个四边形既是%// //%,又是%// //%;满足什么条件的矩形是正方形呢?
满足有一组邻边相等的矩形就是正方形.或满足对角线互相垂直的的矩形也是正方形.
矩形
菱形
【问题3】满足什么条件的菱形是正方形呢?
满足有一个角是直角的菱形就是正方形.或满足对角线相等的菱形也是正方形.
小结:正方形判定定理
(1)一组邻边%// //% 的矩形是正方形;
(2)对角线%// //% 的矩形是正方形;
(3)有一个角是%// //% 的菱形是正方形;
(4)对角线%// //% 的菱形是正方形.
相等
相等
互相垂直
互相垂直
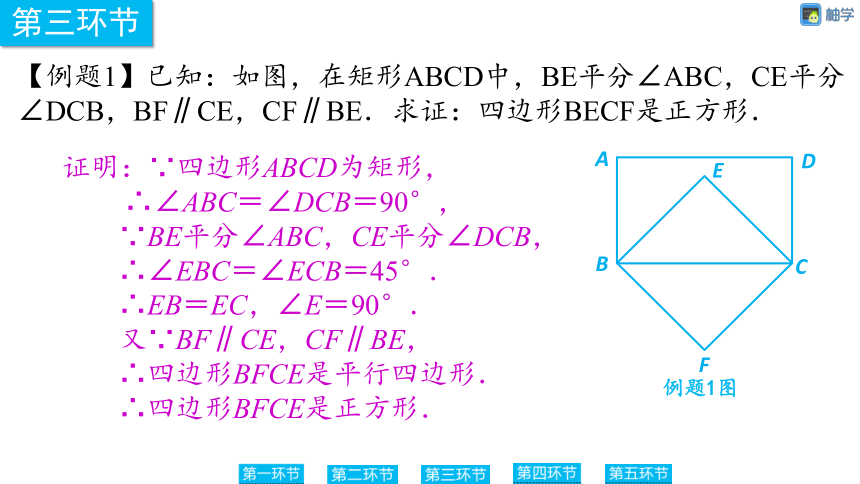
【例题1】已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
C
F
E
A
D
B
例题1图
证明:∵四边形ABCD为矩形,
∴∠ABC=∠DCB=90°,
∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ECB=45°.
∴EB=EC,∠E=90°.
又∵BF∥CE,CF∥BE,
∴四边形BFCE是平行四边形.
∴四边形BFCE是正方形.
C
F
E
A
D
B
H
G
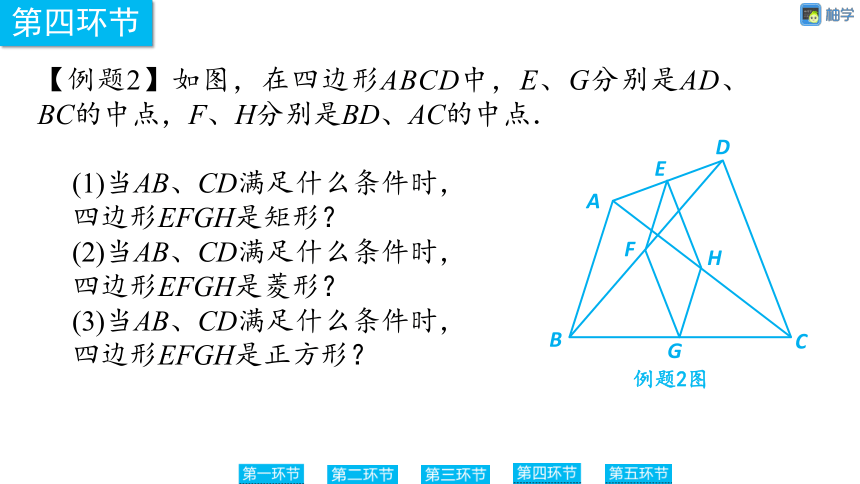
例题2图
【例题2】如图,在四边形ABCD中,E、G分别是AD、BC的中点,F、H分别是BD、AC的中点.
(1)当AB、CD满足什么条件时,
四边形EFGH是矩形?
(2)当AB、CD满足什么条件时,
四边形EFGH是菱形?
(3)当AB、CD满足什么条件时,
四边形EFGH是正方形?
(1)当AB⊥CD时,四边形EFGH是矩形.
证明:∵E、F分别是AD,BD的中点,G、H分别中BC,AC的中点,
∴EF∥AB,EF=AB;GH∥AB,GH=AB.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形,
∵AB⊥CD,∴EF⊥EH,∴∠FEH=90°,
∴四边形EFGH是矩形.
(2)当AB=CD时,四边形EFGH是菱形.
证明:∵E、F分别是AD,BD的中点,H,G分别是AC,BC的中点,
G、F分别是BC,BD的中点,E,H分别是AD,AC的中点,
∴EF=AB,HG=AB,FG=CD,EH=CD,
又∵AB=CD,∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
(3)当四边形ABCD满足AB=CD且AB⊥CD时,
四边形EFGH为正方形,
证明:由(1)(2)可知四边形EFGH是矩形也是菱形
∴四边形EFGH是正方形.
C
F
E
A
D
B
G
H
第1题图
1.如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
解:四边形EFGH是正方形.
证明:∵AE=BF=CG=DH,∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.∴∠EHG=90°.
∴四边形EFGH是正方形.
2.(☆) (中考真题) (1) 如图(1), 正方形的对角线相交于点, 点是正方形的一 个顶点, 已知两个正方形的边长相等, 当正方形绕点转动时, 两个正方形重叠部分的面积相等吗 为什么
解: (1) 相等. 理由如下: 是正方形 的对角线,
在 和 中,
,
四边形 面积 ,
当正方形 绕点 转动时, 两个正方形重叠部分的面积相等.
(2) 如图(2), 与 是两块全等的等腰直角三角板, 当其中一块的直角顶点 在另 一块的斜边中点处时, 绕点 转动, 两块三角板重叠部分的面积相等吗 为什么
(2) 相等. 理由如下: 连接 , 如答图 (1),
是等腰直角三角形, 为 中点,
,
.
在 和 中,
,
四边形 面积 ,
当其中一块的直角顶点 在另一块的斜边中点处时, 绕点 转动, 两块三角板重叠 部分的面积相等.
(3) 如图(3), 将 个边长都为 的正方形按如图所示摆放, 点 分别是正方形的 中心, 则 个这样的正方形重叠部分的面积和为多少
(3) 如答图 (2), 过点 分别作正方形两边的垂线 与 , 点 是正方形的中心,
, 四边形 是正方形,
在 和 中,
, 的面积 的面积,
一个阴影部分的面积 正方形 的面积 , 同理可求,每一个阴影部分的面积都是正方形面积的 , 为 ,
重叠部分的面积和 .
第一章
特殊的平行四边形
第8课
长方形的判定
(1)边的性质:%// //% 等.
(2)角的性质:%// //% 等.
(3)对角线的性质:
两条对角线%// //%,
每条对角线平分%// //%.
(4)对称性:是%// //%,
有%// //%条对称轴,
也是%// //%对称图形.
四条边相等
四个角都是直角
相等且互相垂直平分
一组对角
轴对称图形
4
中心
正方形的性质
【问题1】正方形的定义:有一组邻边 ,
并且有一个角是 的平行四边形是正方形.
相等
直角
【问题2】要证明一个四边形是正方形,就是要证明这个四边形既是%// //%,又是%// //%;满足什么条件的矩形是正方形呢?
满足有一组邻边相等的矩形就是正方形.或满足对角线互相垂直的的矩形也是正方形.
矩形
菱形
【问题3】满足什么条件的菱形是正方形呢?
满足有一个角是直角的菱形就是正方形.或满足对角线相等的菱形也是正方形.
小结:正方形判定定理
(1)一组邻边%// //% 的矩形是正方形;
(2)对角线%// //% 的矩形是正方形;
(3)有一个角是%// //% 的菱形是正方形;
(4)对角线%// //% 的菱形是正方形.
相等
相等
互相垂直
互相垂直
【例题1】已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
C
F
E
A
D
B
例题1图
证明:∵四边形ABCD为矩形,
∴∠ABC=∠DCB=90°,
∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ECB=45°.
∴EB=EC,∠E=90°.
又∵BF∥CE,CF∥BE,
∴四边形BFCE是平行四边形.
∴四边形BFCE是正方形.
C
F
E
A
D
B
H
G
例题2图
【例题2】如图,在四边形ABCD中,E、G分别是AD、BC的中点,F、H分别是BD、AC的中点.
(1)当AB、CD满足什么条件时,
四边形EFGH是矩形?
(2)当AB、CD满足什么条件时,
四边形EFGH是菱形?
(3)当AB、CD满足什么条件时,
四边形EFGH是正方形?
(1)当AB⊥CD时,四边形EFGH是矩形.
证明:∵E、F分别是AD,BD的中点,G、H分别中BC,AC的中点,
∴EF∥AB,EF=AB;GH∥AB,GH=AB.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形,
∵AB⊥CD,∴EF⊥EH,∴∠FEH=90°,
∴四边形EFGH是矩形.
(2)当AB=CD时,四边形EFGH是菱形.
证明:∵E、F分别是AD,BD的中点,H,G分别是AC,BC的中点,
G、F分别是BC,BD的中点,E,H分别是AD,AC的中点,
∴EF=AB,HG=AB,FG=CD,EH=CD,
又∵AB=CD,∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
(3)当四边形ABCD满足AB=CD且AB⊥CD时,
四边形EFGH为正方形,
证明:由(1)(2)可知四边形EFGH是矩形也是菱形
∴四边形EFGH是正方形.
C
F
E
A
D
B
G
H
第1题图
1.如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
解:四边形EFGH是正方形.
证明:∵AE=BF=CG=DH,∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.∴∠EHG=90°.
∴四边形EFGH是正方形.
2.(☆) (中考真题) (1) 如图(1), 正方形的对角线相交于点, 点是正方形的一 个顶点, 已知两个正方形的边长相等, 当正方形绕点转动时, 两个正方形重叠部分的面积相等吗 为什么
解: (1) 相等. 理由如下: 是正方形 的对角线,
在 和 中,
,
四边形 面积 ,
当正方形 绕点 转动时, 两个正方形重叠部分的面积相等.
(2) 如图(2), 与 是两块全等的等腰直角三角板, 当其中一块的直角顶点 在另 一块的斜边中点处时, 绕点 转动, 两块三角板重叠部分的面积相等吗 为什么
(2) 相等. 理由如下: 连接 , 如答图 (1),
是等腰直角三角形, 为 中点,
,
.
在 和 中,
,
四边形 面积 ,
当其中一块的直角顶点 在另一块的斜边中点处时, 绕点 转动, 两块三角板重叠 部分的面积相等.
(3) 如图(3), 将 个边长都为 的正方形按如图所示摆放, 点 分别是正方形的 中心, 则 个这样的正方形重叠部分的面积和为多少
(3) 如答图 (2), 过点 分别作正方形两边的垂线 与 , 点 是正方形的中心,
, 四边形 是正方形,
在 和 中,
, 的面积 的面积,
一个阴影部分的面积 正方形 的面积 , 同理可求,每一个阴影部分的面积都是正方形面积的 , 为 ,
重叠部分的面积和 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
