指数函数及其性质 课件
图片预览





文档简介
课件17张PPT。2.1.2《指数函数及其性质》
1.了解指数函数的实际背景,认识学习指数函数的必要性;
2.理解指数函数的含义,观察图象的变化、探索其性质;
3.引导学生运用知识解决相关问题,发展学生的思维能力。教学目标教学重难点重点:
(1)指数函数的概念和性质及其应用.
(2)指数函数底数a 对图象的影响;
(3)利用指数函数单调性熟练比较几个指 数幂的大小
难点:
(1)利用函数单调性比较指数幂的大小
(2)指数函数性质的归纳,概括及其应用.导入新课新课导入引例1:问题:一种放射性物质不断衰减为其它物质,每经过一年剩留量约为原来的84%,
则这种物质经过x年后的剩留量是原来的
多少?导入新课新课导入引例2:分析:若设该物质原有量为1,则经过一年剩留量为1×84%,经过二年剩留量为1×84% ×84% =0.842,经过三年剩留量为1×84% ×84% ×84% =0.843,……即经过x年后的剩留量是原来的0.84x 对于这个关系式,每给自变量x的一个值,y都有唯一确定的值和它对应.(自变量在指数上;底数是确定的常数,可以大于1也可以大于0小于1)
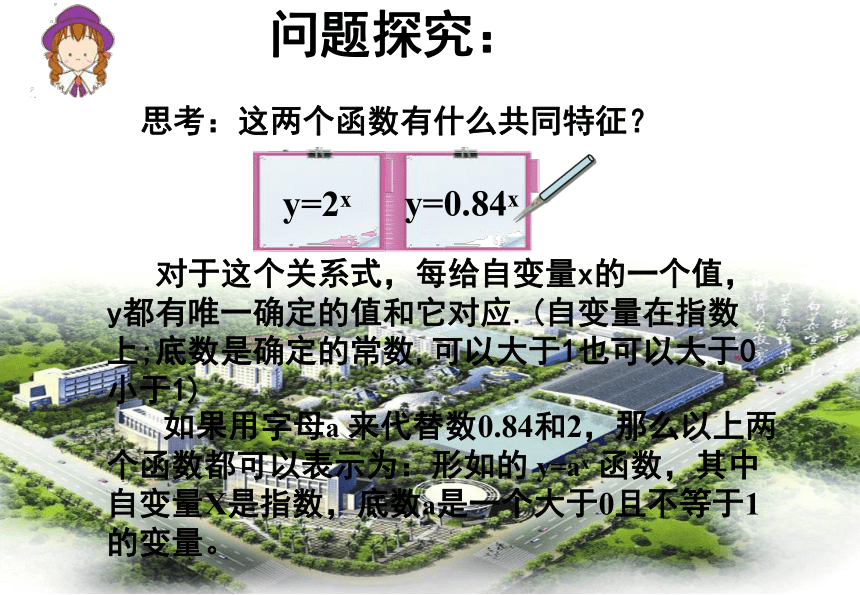
问题探究:思考:这两个函数有什么共同特征?
如果用字母a 来代替数0.84和2,那么以上两个函数都可以表示为:形如的 y=ax 函数,其中自变量X是指数,底数a是一个大于0且不等于1的变量。
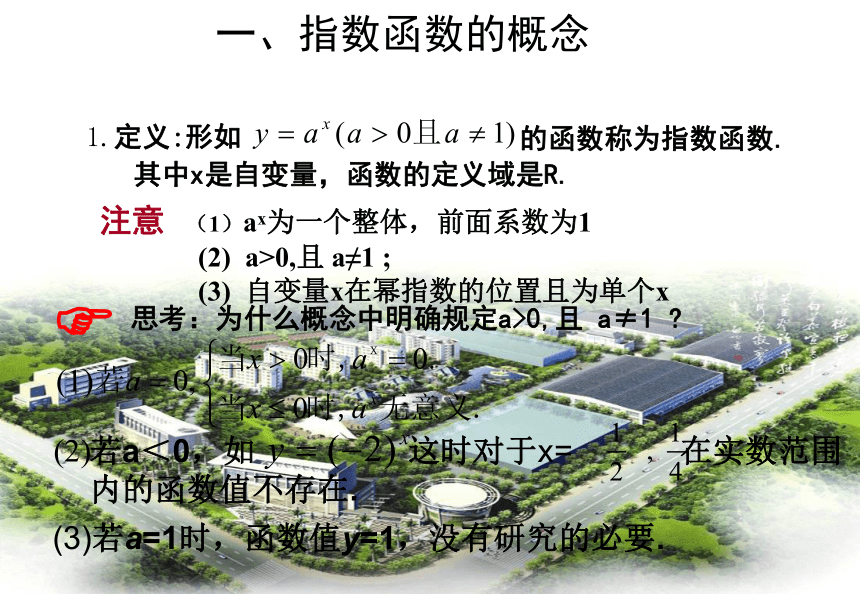
一、指数函数的概念(3)若a=1时,函数值y=1,没有研究的必要.(1)注意 (1)ax为一个整体,前面系数为1
(2) a>0,且 a≠1 ;
(3) 自变量x在幂指数的位置且为单个x
概念考察跟踪练习(1) (5) (6)例1.下列函数是指数函数的是:用描点法作函数 和 的图像y=2x二、指数函数的图像和性质y = 2xy = xyx0 1 2 3 4 5 6 7 88
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3y = 2xy = x(0,1)y = 2xy = 3xy = 4x指数函数的图像和性质(0,1)a越来越大R(0,+∞)(0,1)在R上是增函数在R上是减函数(1)定义域:(2)值域:(3)定点:(4)单调性: (5)
函数
值的
分布
情况指数函数y=ax (a>0,且a≠1)的图象和性质y=1(0,1)xOy例2、比较下列各题中两个值的大小:
(1) 1.72.5,1.73(2) 0.8-0.1,0.8-0.2(3) 1.70.3,0.93.1
课例评析 (3)解(3) :不能看作同一个指数函数的两个函数值,我们可在这两个数值中间找一个数值(中间量)将这一数值与原来两个数值分别比较大小,然后确定原来两个数值的大小关系。根据指数函数的性质,知:且>所以:课例评析变式练习:比较下列各题中两个值的大小:
(1) 22.5,23 (2) 0.5-0.1,0.5-0.2 (3) 1.50.3,0.53.1
比较两个幂值大小的方法:(1)构造指数函数并指明其单调性. (2)自变量的大小比较. (3)函数值的大小比较. 法一:构造函数法: 数的特征是同底数不同指数. 方法提炼法二:寻求中间量: 当底数不同,指数也不同时. 课堂小结1.指数函数的概念2.指数函数的图像和性质3.指数函数性质的简单应用 数形结合,由具体到一般1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数3.在R上是减函数4.非奇非偶函数
x函 数 图 象1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
y0 a>1函数性质思想与方法:y=1(0,1)x在第一象限内,按逆时针方向旋转,底数a越来越大0
1.了解指数函数的实际背景,认识学习指数函数的必要性;
2.理解指数函数的含义,观察图象的变化、探索其性质;
3.引导学生运用知识解决相关问题,发展学生的思维能力。教学目标教学重难点重点:
(1)指数函数的概念和性质及其应用.
(2)指数函数底数a 对图象的影响;
(3)利用指数函数单调性熟练比较几个指 数幂的大小
难点:
(1)利用函数单调性比较指数幂的大小
(2)指数函数性质的归纳,概括及其应用.导入新课新课导入引例1:问题:一种放射性物质不断衰减为其它物质,每经过一年剩留量约为原来的84%,
则这种物质经过x年后的剩留量是原来的
多少?导入新课新课导入引例2:分析:若设该物质原有量为1,则经过一年剩留量为1×84%,经过二年剩留量为1×84% ×84% =0.842,经过三年剩留量为1×84% ×84% ×84% =0.843,……即经过x年后的剩留量是原来的0.84x 对于这个关系式,每给自变量x的一个值,y都有唯一确定的值和它对应.(自变量在指数上;底数是确定的常数,可以大于1也可以大于0小于1)
问题探究:思考:这两个函数有什么共同特征?
如果用字母a 来代替数0.84和2,那么以上两个函数都可以表示为:形如的 y=ax 函数,其中自变量X是指数,底数a是一个大于0且不等于1的变量。
一、指数函数的概念(3)若a=1时,函数值y=1,没有研究的必要.(1)注意 (1)ax为一个整体,前面系数为1
(2) a>0,且 a≠1 ;
(3) 自变量x在幂指数的位置且为单个x
概念考察跟踪练习(1) (5) (6)例1.下列函数是指数函数的是:用描点法作函数 和 的图像y=2x二、指数函数的图像和性质y = 2xy = xyx0 1 2 3 4 5 6 7 88
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3y = 2xy = x(0,1)y = 2xy = 3xy = 4x指数函数的图像和性质(0,1)a越来越大R(0,+∞)(0,1)在R上是增函数在R上是减函数(1)定义域:(2)值域:(3)定点:(4)单调性: (5)
函数
值的
分布
情况指数函数y=ax (a>0,且a≠1)的图象和性质y=1(0,1)xOy例2、比较下列各题中两个值的大小:
(1) 1.72.5,1.73(2) 0.8-0.1,0.8-0.2(3) 1.70.3,0.93.1
课例评析 (3)解(3) :不能看作同一个指数函数的两个函数值,我们可在这两个数值中间找一个数值(中间量)将这一数值与原来两个数值分别比较大小,然后确定原来两个数值的大小关系。根据指数函数的性质,知:且>所以:课例评析变式练习:比较下列各题中两个值的大小:
(1) 22.5,23 (2) 0.5-0.1,0.5-0.2 (3) 1.50.3,0.53.1
比较两个幂值大小的方法:(1)构造指数函数并指明其单调性. (2)自变量的大小比较. (3)函数值的大小比较. 法一:构造函数法: 数的特征是同底数不同指数. 方法提炼法二:寻求中间量: 当底数不同,指数也不同时. 课堂小结1.指数函数的概念2.指数函数的图像和性质3.指数函数性质的简单应用 数形结合,由具体到一般1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数3.在R上是减函数4.非奇非偶函数
x函 数 图 象1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
y0 a>1函数性质思想与方法:y=1(0,1)x在第一象限内,按逆时针方向旋转,底数a越来越大0
