1.6三角函数模型的简单应用(下)
文档属性
| 名称 | 1.6三角函数模型的简单应用(下) |  | |
| 格式 | zip | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-05 21:16:21 | ||
图片预览


文档简介
课件18张PPT。高一数学新授课 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作1.6 三角函数模型
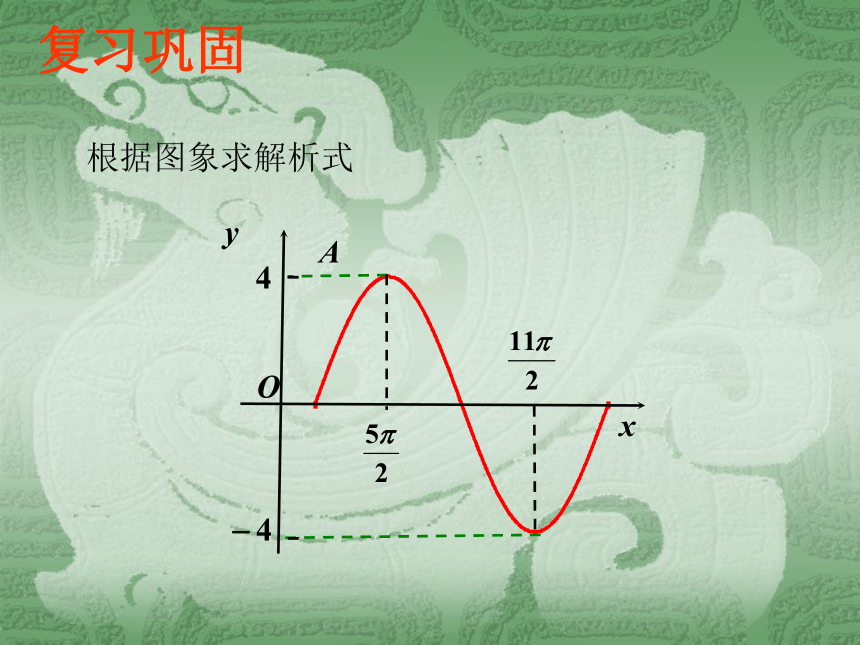
的简单应用(下)复习巩固根据图象求解析式问题提出 2.三角函数的应用十分广泛, 对于与角有关的实际问题,我们可以建立一个三角函数,通过研究其图象和性质或进行定量分析,就能解决相应问题.这是一种数学思想,需要结合具体问题的研究才能领会和掌握.例3 如图,设地球表面某地正午太阳高度
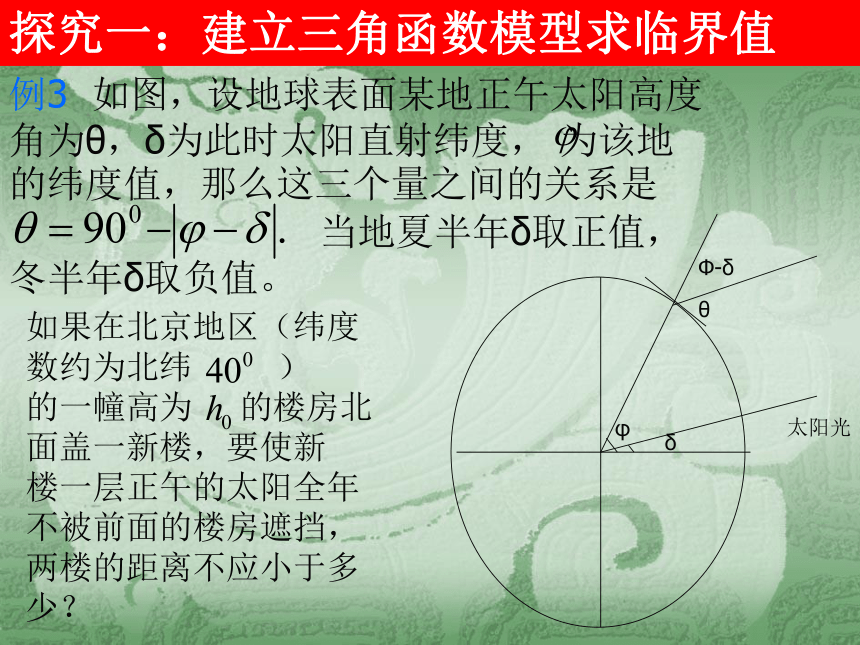
角为θ,δ为此时太阳直射纬度, 为该地
的纬度值,那么这三个量之间的关系是
当地夏半年δ取正值,
冬半年δ取负值。如果在北京地区(纬度数约为北纬 )
的一幢高为 的楼房北面盖一新楼,要使新
楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?
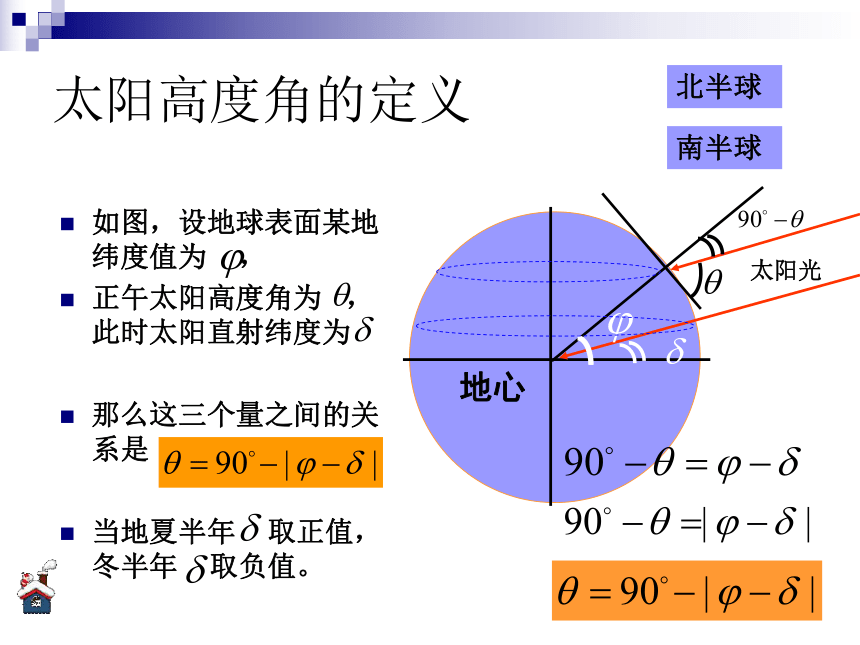
探究一:建立三角函数模型求临界值 太阳高度角的定义如图,设地球表面某地纬度值为 ,
正午太阳高度角为 ,此时太阳直射纬度为
那么这三个量之间的关系是
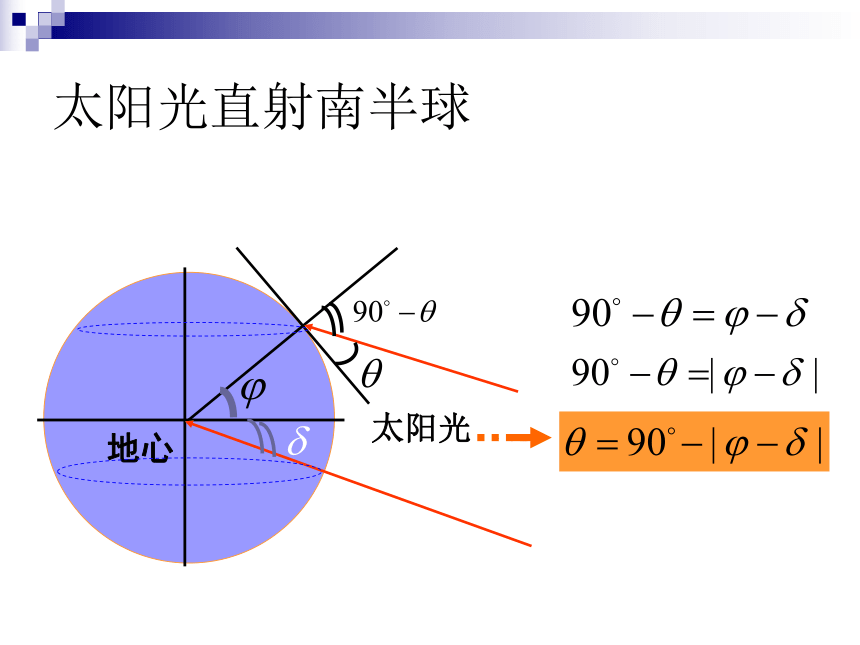
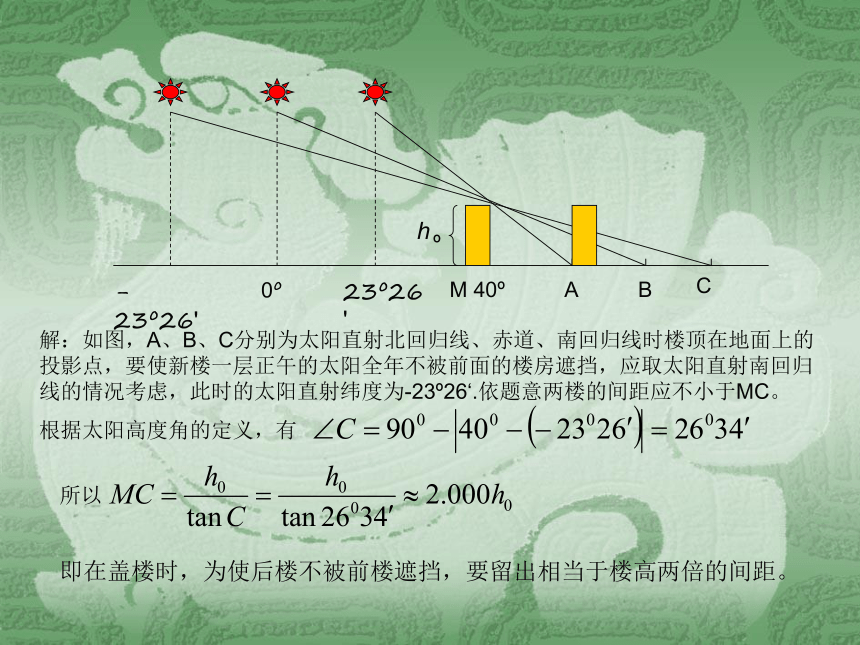
当地夏半年 取正值,冬半年 取负值。太阳光地心北半球南半球太阳光直射南半球太阳光地心C-23o26'ABM 40o0o23o26'ho解:如图,A、B、C分别为太阳直射北回归线、赤道、南回归线时楼顶在地面上的投影点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线的情况考虑,此时的太阳直射纬度为-23o26‘.依题意两楼的间距应不小于MC。
根据太阳高度角的定义,有所以即在盖楼时,为使后楼不被前楼遮挡,要留出相当于楼高两倍的间距。注意 实际问题的背景往往比较复杂,而且需要综合应用多学科的知识才能解决它.因此在应用数学知识解决实际问题时,应当注意从复杂的背景中抽取基本的数学关系,还要调动相关学科知识来帮助理解问题。三角应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图②建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解三角形的
数学模型.③求解:利用三角形,求得数学模型的解.④检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.即解三角应用题的基本思路练习2:小王想在”大叶池”小区买房,该小区的楼高7层,每层3米,楼与楼之间相距15米。要使所买楼层在一年四季正午太阳不被前面的楼房遮挡,他应选择哪几层的房?3层以上练习1:绍兴市的纬度是北纬300 ,开发商在某小区建若干幢楼,楼高7层,每层3米。要使所建楼房一楼在一年四季正午太阳不被南面的楼房遮挡,两楼间的距离不应小于多少? 例4.海水受日月的引力,在一定的时候发生涨落的现象叫潮,
一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋,下面是某港口
在某季节每天的时间与水深的关系表:
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,
并给出整点时的水深的近似数值。(精确到0.001)
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例
规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能
进入港口?在港口能呆多久?
(3)若某船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始
卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必
须停止卸货,将船驶向较深的水域?探究二:根据相关数据进行三角函数拟合(1)以时间为横坐标,水深为纵坐标,
在直角坐标系中画出散点图,根据图象,
可以考虑用函数
来刻画水深与时间之间的对应关系.
从数据和图象可以得出:A=2.5,h=5,T=12, =0;由 ,得所以,这个港口的水深与时间的关系可以近似描述为:由上述关系式易得港口在整点时水深的近似值:解:
(2)货船需要的安全水深
为 4+1.5=5.5 (米),所以
当y≥5.5时就可以进港.
令
化简得由计算器计算可得解得因为 ,所以有函数周期性易得因此,货船可以在凌晨零时30分左右进港,早晨5时30分左右出
港;或在中午12时30分左右进港,下午17时30分左右出港,每次
可以在港口停留5小时左右。解:解:(3)设在时刻x船舶的安全水深为y,
那么y=5.5-0.3(x-2) (x≥2),在同一坐标
系内作出这两个函数的图象,可以看
到在6时到7时之间两个函数图象有一
个交点.通过计算可得在6时的水深约为5米,此时船舶的安全水深约为
4.3米;6.5时的水深约为4.2米,此时船舶的安全水深约为4.1米;
7时的水深约为3.8米,而船舶的安全水深约为4米,因此为了安
全,船舶最好在6.5时之前停止卸货,将船舶驶向较深的水域。对于现实世界中具有周期现象的实际问题,可以利用三角函数模型描述其变化规律.可分为三阶段:第一阶段:收集数据,画图;第二阶段:选择函数类型,并求得函数类型;第三阶段:将函数模型应用的实际中小结:三阶段:收集数据,画图选择函数类型,求得函数类型应用于实际 在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m,一次高潮发生在4:00.每天涨潮落潮时,水的深度y(m)与时间t(h)近似满足关系式
(1)若从0:00开始计算时间,选用一个三角函数来 近似描述该港口的水深y和t之间的函数关系
(2)17:00该港口的水深为多少?(保留一位有效数字)
(3)这一天有多少小时水深低于10.3m?
练习1 练习2 如图,甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东θ角方向直线航行,并与乙船在C处相遇,求甲船的航速.总 结对于现实世界中具有周期现象的实际问题,可以利用三角函数模型描述其变化规律.先根据相关数据作出散点图,再进行函数拟合,就可获得具体的函数模型,有了这个函数模型就可以解决相应的实际问题.
三角应用题的一般步骤是:搜集数据 由数据图形 利用函数模型
画出示意图 得出函数模型 解决实际问题→→作业:
P71复习参考题B组:
2,3,4,7,8.
高中数学老师欧阳文丰制作1.6 三角函数模型
的简单应用(下)复习巩固根据图象求解析式问题提出 2.三角函数的应用十分广泛, 对于与角有关的实际问题,我们可以建立一个三角函数,通过研究其图象和性质或进行定量分析,就能解决相应问题.这是一种数学思想,需要结合具体问题的研究才能领会和掌握.例3 如图,设地球表面某地正午太阳高度
角为θ,δ为此时太阳直射纬度, 为该地
的纬度值,那么这三个量之间的关系是
当地夏半年δ取正值,
冬半年δ取负值。如果在北京地区(纬度数约为北纬 )
的一幢高为 的楼房北面盖一新楼,要使新
楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?
探究一:建立三角函数模型求临界值 太阳高度角的定义如图,设地球表面某地纬度值为 ,
正午太阳高度角为 ,此时太阳直射纬度为
那么这三个量之间的关系是
当地夏半年 取正值,冬半年 取负值。太阳光地心北半球南半球太阳光直射南半球太阳光地心C-23o26'ABM 40o0o23o26'ho解:如图,A、B、C分别为太阳直射北回归线、赤道、南回归线时楼顶在地面上的投影点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线的情况考虑,此时的太阳直射纬度为-23o26‘.依题意两楼的间距应不小于MC。
根据太阳高度角的定义,有所以即在盖楼时,为使后楼不被前楼遮挡,要留出相当于楼高两倍的间距。注意 实际问题的背景往往比较复杂,而且需要综合应用多学科的知识才能解决它.因此在应用数学知识解决实际问题时,应当注意从复杂的背景中抽取基本的数学关系,还要调动相关学科知识来帮助理解问题。三角应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图②建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解三角形的
数学模型.③求解:利用三角形,求得数学模型的解.④检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.即解三角应用题的基本思路练习2:小王想在”大叶池”小区买房,该小区的楼高7层,每层3米,楼与楼之间相距15米。要使所买楼层在一年四季正午太阳不被前面的楼房遮挡,他应选择哪几层的房?3层以上练习1:绍兴市的纬度是北纬300 ,开发商在某小区建若干幢楼,楼高7层,每层3米。要使所建楼房一楼在一年四季正午太阳不被南面的楼房遮挡,两楼间的距离不应小于多少? 例4.海水受日月的引力,在一定的时候发生涨落的现象叫潮,
一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋,下面是某港口
在某季节每天的时间与水深的关系表:
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,
并给出整点时的水深的近似数值。(精确到0.001)
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例
规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能
进入港口?在港口能呆多久?
(3)若某船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始
卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必
须停止卸货,将船驶向较深的水域?探究二:根据相关数据进行三角函数拟合(1)以时间为横坐标,水深为纵坐标,
在直角坐标系中画出散点图,根据图象,
可以考虑用函数
来刻画水深与时间之间的对应关系.
从数据和图象可以得出:A=2.5,h=5,T=12, =0;由 ,得所以,这个港口的水深与时间的关系可以近似描述为:由上述关系式易得港口在整点时水深的近似值:解:
(2)货船需要的安全水深
为 4+1.5=5.5 (米),所以
当y≥5.5时就可以进港.
令
化简得由计算器计算可得解得因为 ,所以有函数周期性易得因此,货船可以在凌晨零时30分左右进港,早晨5时30分左右出
港;或在中午12时30分左右进港,下午17时30分左右出港,每次
可以在港口停留5小时左右。解:解:(3)设在时刻x船舶的安全水深为y,
那么y=5.5-0.3(x-2) (x≥2),在同一坐标
系内作出这两个函数的图象,可以看
到在6时到7时之间两个函数图象有一
个交点.通过计算可得在6时的水深约为5米,此时船舶的安全水深约为
4.3米;6.5时的水深约为4.2米,此时船舶的安全水深约为4.1米;
7时的水深约为3.8米,而船舶的安全水深约为4米,因此为了安
全,船舶最好在6.5时之前停止卸货,将船舶驶向较深的水域。对于现实世界中具有周期现象的实际问题,可以利用三角函数模型描述其变化规律.可分为三阶段:第一阶段:收集数据,画图;第二阶段:选择函数类型,并求得函数类型;第三阶段:将函数模型应用的实际中小结:三阶段:收集数据,画图选择函数类型,求得函数类型应用于实际 在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m,一次高潮发生在4:00.每天涨潮落潮时,水的深度y(m)与时间t(h)近似满足关系式
(1)若从0:00开始计算时间,选用一个三角函数来 近似描述该港口的水深y和t之间的函数关系
(2)17:00该港口的水深为多少?(保留一位有效数字)
(3)这一天有多少小时水深低于10.3m?
练习1 练习2 如图,甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东θ角方向直线航行,并与乙船在C处相遇,求甲船的航速.总 结对于现实世界中具有周期现象的实际问题,可以利用三角函数模型描述其变化规律.先根据相关数据作出散点图,再进行函数拟合,就可获得具体的函数模型,有了这个函数模型就可以解决相应的实际问题.
三角应用题的一般步骤是:搜集数据 由数据图形 利用函数模型
画出示意图 得出函数模型 解决实际问题→→作业:
P71复习参考题B组:
2,3,4,7,8.
