2.6.2双曲线的几何性质 教案(表格式)
文档属性
| 名称 | 2.6.2双曲线的几何性质 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 118.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览

文档简介
双曲线的几何性质
教学目标 知识与技能 1.了解双曲线的简单几何性质,如范围、对称性、顶点、渐近线和离心率等。2.能用双曲线的简单几何性质解决一些简单问题。
教学重难点 双曲线的几何性质及初步运用
教学过程
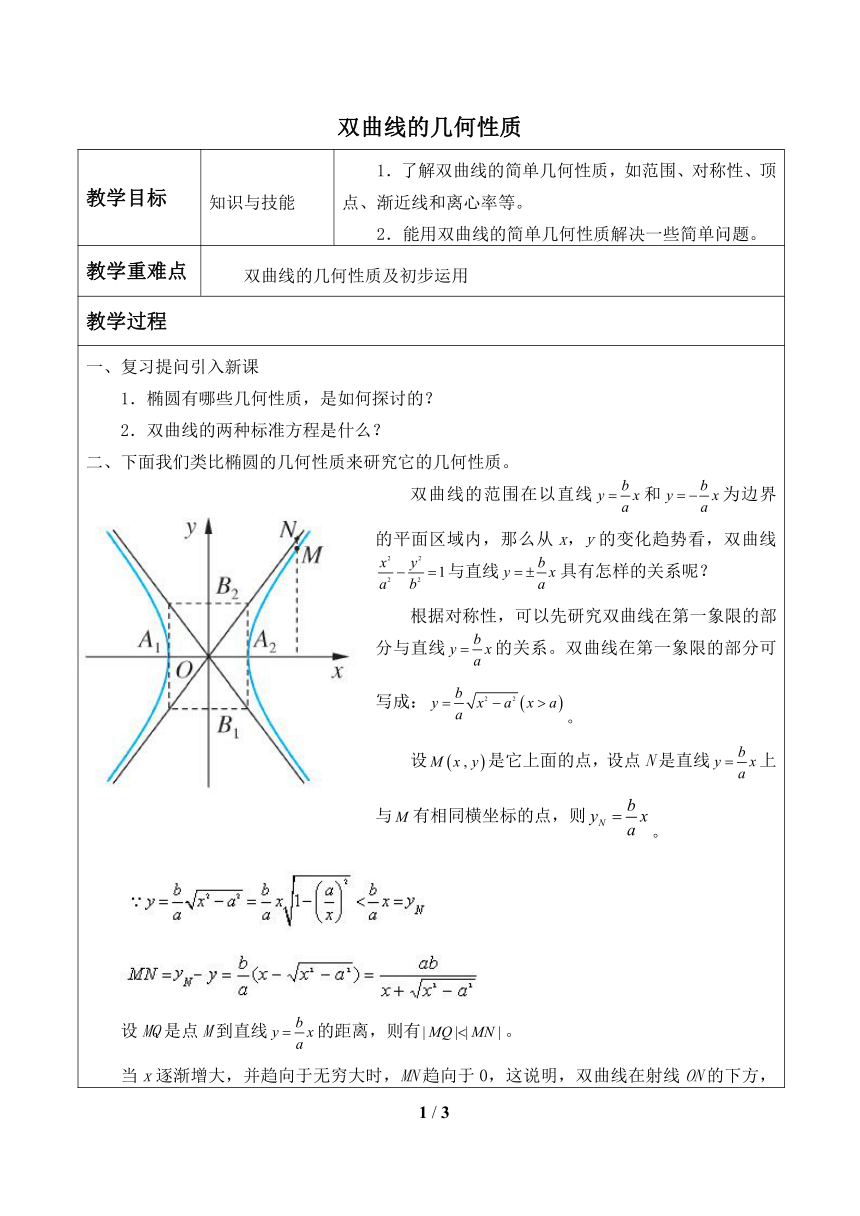
一、复习提问引入新课1.椭圆有哪些几何性质,是如何探讨的?2.双曲线的两种标准方程是什么?二、下面我们类比椭圆的几何性质来研究它的几何性质。双曲线的范围在以直线和为边界的平面区域内,那么从x,y的变化趋势看,双曲线与直线具有怎样的关系呢?根据对称性,可以先研究双曲线在第一象限的部分与直线的关系。双曲线在第一象限的部分可写成:。设是它上面的点,设点N是直线上与有相同横坐标的点,则。设MQ是点M到直线的距离,则有。当x逐渐增大,并趋向于无穷大时,MN趋向于0,这说明,双曲线在射线ON的下方,并无限接近于射线ON在其他象限内也可以证明类似的情况我们把两条直线叫做双曲线的渐近线定义:直线叫做双曲线的渐近线;直线叫做双曲线的渐近线三、离心率由于正确认识了渐近线的概念,对于离心率的直观意义也就容易掌握了,为此,介绍一下双曲线的离心率以及它对双曲线的形状的影响:1.双曲线的焦距与实轴的比叫做双曲线的离心率,且2.由于,所以越大,也越大,即渐近线的斜率绝对值越大。这时双曲线的形状就从扁小逐渐变得开阔,从而得出:双曲线的离心率越大,它的开口就越开阔这时,指出:焦点在y轴上的双曲线的几何性质可以类似得出,双曲线的几何性质与坐标系的选择无关,即不随坐标系的改变而改变四、例题讲解1.求双曲线的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程:分析:由双曲线的标准方程,容易求出,引导学生用双曲线的实轴长、虚轴长、离心率、焦点和渐近线的定义即可求相关量或式子,但要注意焦点在y轴上的渐近线是。2.已知双曲线的中心在原点,焦点在y轴上,焦距为16,离心率为,求双曲线的标准方程3.(1)求与双曲线的渐近线,且经过点的双曲线的标准方程及离心率(2)求与双曲线有公共焦点,且过点的双曲线的标准方程分析:已知双曲线的渐近线,求双曲线的标准方程:方法一按焦点位置分别设方程求解;方法二可直接设所求的双曲线的方程为作业布置1.已知双曲线方程如下,求它们的两个焦点、离心率e和渐近线方程。(1); (2)2.求双曲线的标准方程:(1)实轴的长是10,虚轴长是8,焦点在x轴上;(2)焦距是10,虚轴长是8,焦点在y轴上;(3)离心率,经过点; (4)两条渐近线的方程是,经过点。3.求以椭圆的焦点为顶点,而以椭圆的顶点为焦点的双曲线的方程。
3 / 3
教学目标 知识与技能 1.了解双曲线的简单几何性质,如范围、对称性、顶点、渐近线和离心率等。2.能用双曲线的简单几何性质解决一些简单问题。
教学重难点 双曲线的几何性质及初步运用
教学过程
一、复习提问引入新课1.椭圆有哪些几何性质,是如何探讨的?2.双曲线的两种标准方程是什么?二、下面我们类比椭圆的几何性质来研究它的几何性质。双曲线的范围在以直线和为边界的平面区域内,那么从x,y的变化趋势看,双曲线与直线具有怎样的关系呢?根据对称性,可以先研究双曲线在第一象限的部分与直线的关系。双曲线在第一象限的部分可写成:。设是它上面的点,设点N是直线上与有相同横坐标的点,则。设MQ是点M到直线的距离,则有。当x逐渐增大,并趋向于无穷大时,MN趋向于0,这说明,双曲线在射线ON的下方,并无限接近于射线ON在其他象限内也可以证明类似的情况我们把两条直线叫做双曲线的渐近线定义:直线叫做双曲线的渐近线;直线叫做双曲线的渐近线三、离心率由于正确认识了渐近线的概念,对于离心率的直观意义也就容易掌握了,为此,介绍一下双曲线的离心率以及它对双曲线的形状的影响:1.双曲线的焦距与实轴的比叫做双曲线的离心率,且2.由于,所以越大,也越大,即渐近线的斜率绝对值越大。这时双曲线的形状就从扁小逐渐变得开阔,从而得出:双曲线的离心率越大,它的开口就越开阔这时,指出:焦点在y轴上的双曲线的几何性质可以类似得出,双曲线的几何性质与坐标系的选择无关,即不随坐标系的改变而改变四、例题讲解1.求双曲线的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程:分析:由双曲线的标准方程,容易求出,引导学生用双曲线的实轴长、虚轴长、离心率、焦点和渐近线的定义即可求相关量或式子,但要注意焦点在y轴上的渐近线是。2.已知双曲线的中心在原点,焦点在y轴上,焦距为16,离心率为,求双曲线的标准方程3.(1)求与双曲线的渐近线,且经过点的双曲线的标准方程及离心率(2)求与双曲线有公共焦点,且过点的双曲线的标准方程分析:已知双曲线的渐近线,求双曲线的标准方程:方法一按焦点位置分别设方程求解;方法二可直接设所求的双曲线的方程为作业布置1.已知双曲线方程如下,求它们的两个焦点、离心率e和渐近线方程。(1); (2)2.求双曲线的标准方程:(1)实轴的长是10,虚轴长是8,焦点在x轴上;(2)焦距是10,虚轴长是8,焦点在y轴上;(3)离心率,经过点; (4)两条渐近线的方程是,经过点。3.求以椭圆的焦点为顶点,而以椭圆的顶点为焦点的双曲线的方程。
3 / 3
