2022.6湖南普通高中学业水平合格性考试数学试卷1(PDF版含答案)
文档属性
| 名称 | 2022.6湖南普通高中学业水平合格性考试数学试卷1(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 09:01:37 | ||
图片预览


文档简介
湖南省 2022 年普通高中学业水平合格性考试
数学仿真模拟试卷(一)
本试卷包括选择题、填空题、和解答题三部分。时量 90 分钟,满分 100 分
一、选择题(本大题共 18 小题,每小题 3 分,满分 54 分。每小题 4 个选项中,只有 1个选项符合题目要
求,多选不给分)
1、如图,将装有水的长方体水槽固定底面一边固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形
成的几何体是( )
A.棱柱
B.棱台
C.棱柱与棱锥的组合体
D.不能确定
2、设全集 I={0,1,2,3}, IM={0,2},则 M=( )
A.{3} B.{1,3} C.{2,3} D.Φ
“ x>0, ”
3 1、 是“ >0” 的( )
y>0
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分又不必要条件
4、下列图形中,表示 M N 的是( )
A、 M N B、 N M
B、 M N D、 M N
1 1
5、甲、乙两人下棋,两人下成和棋的概率是 ,甲获胜的概率是 ,则甲不输的概率为( )
2 3
5 2 1 1
A、 B、 C、 D、
6 5 6 3
6、命题“ x ∈ R,|x|+x2 ≥0”的否定是( )
2 2
A、 x ∈ R,|x|+x <0 B、 x ∈ R,|x|+x ≤ 0
2 2
C、 x ∈ R,|x|+x <0 D、 x ∈ R,|x|+x ≥ 0
7、盒子里装有大小相同的 4 个红球和 6 个白球,从中随机陬出 1 个球,取到白球的概率是( )
3 1 2 2
A、 B、 C、 D、
5 2 3 5
3
8、已知函数 f(x)=x +3x,若 f(-a)=2,则 f(a)的值为( )
A、2 B、-2 C、1 D、-1
9、已知实数 x、y满足 x2+y2=1,则 xy 的最大值是( )
3 2 1
A、1 B、 C、 D、
2 2 2
10、已知角 a=15°,则 a 的弧度数为( )
A、 B、 C、 D、
3 6 8 12
11、某中学有高中生 480 人,初中生 240 人,为了了解学生的身体状况,采用分层抽样的方法,从该校学
生中抽取容量为 n 的样本,其中高中生有 12 人,那么 n 等于( )
A、6 B、9 C、12 D、18
12、 函数 f(x)=x2-5 的零点所在的区间是( )
A、(1,2) B、(2,3) C、(3,4) D、(4,5)
13、为了了解所加工的一批零件的长度,抽测了其中 200 个零件的长度,在这个问题中,200 个零件的长
度是( )
A、总体 B、个体 C、总体的一个样本 D、样本量
14、若复数 Z=3-4i 的模为 a,虚部为 b,则 a+b等于( )
A、5+4i B、5-4i C、1 D、9
2
15、已知命题 p: x∈R,ax +2x+3>0,若命题 p 为假命题,则实数 a 的取值范围是( )
1 1
A、{a|a< } B、{a|03 3
1 1
C、{a|a≤ } D、{a|a≥ }
3 3
16、在 ABC 中,若 BC=3,AC=3 3,A=30°,则 B=( )
A、30° B、60° C、60° 或 120° D、30°或 150°
17、已知 A+B=45°,则(1+tan )(1+tan )的值为
A、2 B、1 C、-2 D、不确定
18、袋内装的红、白、黑球分别有 3,2,1 个,从中任取两个球,则互斥而不对立的事件是( )A、
至少一个白球;都是白球
B、至少一个白球;至少一个黑球
C、至少一个白球;一个白球,一个黑球
D、至少一个白球;红球、黑球各一个
二、填空题(本大题共 4 小题,每小题 4 分,满分 16 分,把答案填在题中的横线上).
19、已知 sinx=1,x [0,2π],则 x 等于
20、若 m<5,且数据 2,3,5,m 的极差为 4,则 m=
1 3
21、i 是虚数单位,复数 = .
1
22、已知集合 A={1,2,a},B={1,3},若 B A,则 a=
三、解答题(每小题 10 分,共 3 小题,满分 30 分).
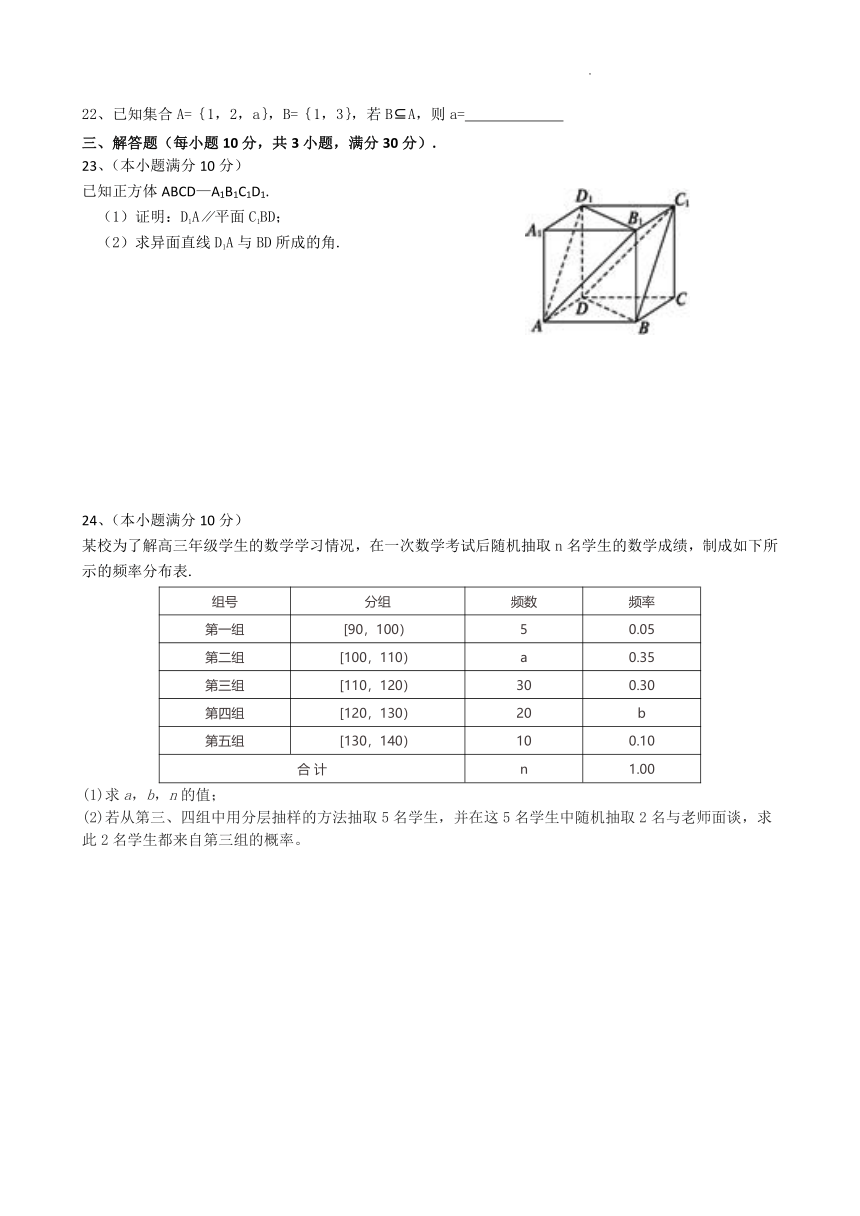
23、(本小题满分 10 分)
已知正方体 ABCD—A1B1C1D1.
(1)证明:D1A∥平面 C1BD;
(2)求异面直线 D1A 与 BD 所成的角.
24、(本小题满分 10 分)
某校为了解高三年级学生的数学学习情况,在一次数学考试后随机抽取 n 名学生的数学成绩,制成如下所
示的频率分布表.
组号 分组 频数 频率
第一组 [90,100) 5 0.05
第二组 [100,110) a 0.35
第三组 [110,120) 30 0.30
第四组 [120,130) 20 b
第五组 [130,140) 10 0.10
合 计 n 1.00
(1)求 a,b,n 的值;
(2)若从第三、四组中用分层抽样的方法抽取 5 名学生,并在这 5 名学生中随机抽取 2 名与老师面谈,求
此 2名学生都来自第三组的概率。
25、(本小题满分 10 分)
已知函数 f(x)=2sin( x+ ).
4
(1)求使函数 f(x)取最小值时 x 的值,并求出 f(x)的最小值;
2
(2)若 f(a)= ,求 sin2a 的值.
3
参考答案:
一、选择题
1-6 ABACAC 7-12 ABDDDA 13-18 CCCCAD
二、填空题
19 、 20、1 21、2-i 22、3
2
三、解答题
23、解:(1)在正方体 ABCD-A1B1C1D1中, ∵AB∥D1C1,AB=D1C1, ∴四边形 ABC1D1是平行四边形,
∴AD1∥BC1, ∵AD1 平面 C1BD,BC1 平面 C1BD, ∴D1A∥平面 C1BD
(2) 由(1)知,AD1∥BC1, ∴异面直线 D1A 与 BD 所成的角即为∠C1BD,
由题可知,△C1BD 为等边三角形, ∴∠C1BD=60°, 即异面直线 D1A 与 BD 所成的角为 60°
5 20
24、解:(1)依题意:得 = 0.05, = 0.35, = b,解得 n=100,a=35,b=0.2;
(2)因为第三,四组共有 50 名学生,用分层抽样的方法抽取 5名学生,则第三,四组分别抽取 3名,2 名,
第三组的 3 名学生记为 a1,a2、a3,第四组的 2 名学生记为 b1、b2,则从 5 名学生中随机抽取 2 名,共有
10 种不同取法,具体如下;{a1,a2},(a1,a3},(a1,b1},{a1,b2},{a2,a3},{a2,b1},{a2,b2},{a3,
b1},{a3,b2},{b1,b2},
3
其中全部来自第三组的情况有 3种,具体如下:{a1,a2},{a1,a3},{a2,a3},故所求概率为10
3
25、解:(1)因为 f(x)=2sin(x+ )所以当 sin(x+ )=-l,即 x+ = 2kπ- ,得 x=2kπ一 (k∈Z)时,f(x)
4 4 4 2 4
有最小值一 2:
2 2
(2)由 f(a)= ,得 2sin(a+ )= ,即 sina+cosa = 1 1 8,两边平方,得 1+sin2a = ,所以 sin2a=- .
3 4 3 3 9 9
数学仿真模拟试卷(一)
本试卷包括选择题、填空题、和解答题三部分。时量 90 分钟,满分 100 分
一、选择题(本大题共 18 小题,每小题 3 分,满分 54 分。每小题 4 个选项中,只有 1个选项符合题目要
求,多选不给分)
1、如图,将装有水的长方体水槽固定底面一边固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形
成的几何体是( )
A.棱柱
B.棱台
C.棱柱与棱锥的组合体
D.不能确定
2、设全集 I={0,1,2,3}, IM={0,2},则 M=( )
A.{3} B.{1,3} C.{2,3} D.Φ
“ x>0, ”
3 1、 是“ >0” 的( )
y>0
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分又不必要条件
4、下列图形中,表示 M N 的是( )
A、 M N B、 N M
B、 M N D、 M N
1 1
5、甲、乙两人下棋,两人下成和棋的概率是 ,甲获胜的概率是 ,则甲不输的概率为( )
2 3
5 2 1 1
A、 B、 C、 D、
6 5 6 3
6、命题“ x ∈ R,|x|+x2 ≥0”的否定是( )
2 2
A、 x ∈ R,|x|+x <0 B、 x ∈ R,|x|+x ≤ 0
2 2
C、 x ∈ R,|x|+x <0 D、 x ∈ R,|x|+x ≥ 0
7、盒子里装有大小相同的 4 个红球和 6 个白球,从中随机陬出 1 个球,取到白球的概率是( )
3 1 2 2
A、 B、 C、 D、
5 2 3 5
3
8、已知函数 f(x)=x +3x,若 f(-a)=2,则 f(a)的值为( )
A、2 B、-2 C、1 D、-1
9、已知实数 x、y满足 x2+y2=1,则 xy 的最大值是( )
3 2 1
A、1 B、 C、 D、
2 2 2
10、已知角 a=15°,则 a 的弧度数为( )
A、 B、 C、 D、
3 6 8 12
11、某中学有高中生 480 人,初中生 240 人,为了了解学生的身体状况,采用分层抽样的方法,从该校学
生中抽取容量为 n 的样本,其中高中生有 12 人,那么 n 等于( )
A、6 B、9 C、12 D、18
12、 函数 f(x)=x2-5 的零点所在的区间是( )
A、(1,2) B、(2,3) C、(3,4) D、(4,5)
13、为了了解所加工的一批零件的长度,抽测了其中 200 个零件的长度,在这个问题中,200 个零件的长
度是( )
A、总体 B、个体 C、总体的一个样本 D、样本量
14、若复数 Z=3-4i 的模为 a,虚部为 b,则 a+b等于( )
A、5+4i B、5-4i C、1 D、9
2
15、已知命题 p: x∈R,ax +2x+3>0,若命题 p 为假命题,则实数 a 的取值范围是( )
1 1
A、{a|a< } B、{a|0
1 1
C、{a|a≤ } D、{a|a≥ }
3 3
16、在 ABC 中,若 BC=3,AC=3 3,A=30°,则 B=( )
A、30° B、60° C、60° 或 120° D、30°或 150°
17、已知 A+B=45°,则(1+tan )(1+tan )的值为
A、2 B、1 C、-2 D、不确定
18、袋内装的红、白、黑球分别有 3,2,1 个,从中任取两个球,则互斥而不对立的事件是( )A、
至少一个白球;都是白球
B、至少一个白球;至少一个黑球
C、至少一个白球;一个白球,一个黑球
D、至少一个白球;红球、黑球各一个
二、填空题(本大题共 4 小题,每小题 4 分,满分 16 分,把答案填在题中的横线上).
19、已知 sinx=1,x [0,2π],则 x 等于
20、若 m<5,且数据 2,3,5,m 的极差为 4,则 m=
1 3
21、i 是虚数单位,复数 = .
1
22、已知集合 A={1,2,a},B={1,3},若 B A,则 a=
三、解答题(每小题 10 分,共 3 小题,满分 30 分).
23、(本小题满分 10 分)
已知正方体 ABCD—A1B1C1D1.
(1)证明:D1A∥平面 C1BD;
(2)求异面直线 D1A 与 BD 所成的角.
24、(本小题满分 10 分)
某校为了解高三年级学生的数学学习情况,在一次数学考试后随机抽取 n 名学生的数学成绩,制成如下所
示的频率分布表.
组号 分组 频数 频率
第一组 [90,100) 5 0.05
第二组 [100,110) a 0.35
第三组 [110,120) 30 0.30
第四组 [120,130) 20 b
第五组 [130,140) 10 0.10
合 计 n 1.00
(1)求 a,b,n 的值;
(2)若从第三、四组中用分层抽样的方法抽取 5 名学生,并在这 5 名学生中随机抽取 2 名与老师面谈,求
此 2名学生都来自第三组的概率。
25、(本小题满分 10 分)
已知函数 f(x)=2sin( x+ ).
4
(1)求使函数 f(x)取最小值时 x 的值,并求出 f(x)的最小值;
2
(2)若 f(a)= ,求 sin2a 的值.
3
参考答案:
一、选择题
1-6 ABACAC 7-12 ABDDDA 13-18 CCCCAD
二、填空题
19 、 20、1 21、2-i 22、3
2
三、解答题
23、解:(1)在正方体 ABCD-A1B1C1D1中, ∵AB∥D1C1,AB=D1C1, ∴四边形 ABC1D1是平行四边形,
∴AD1∥BC1, ∵AD1 平面 C1BD,BC1 平面 C1BD, ∴D1A∥平面 C1BD
(2) 由(1)知,AD1∥BC1, ∴异面直线 D1A 与 BD 所成的角即为∠C1BD,
由题可知,△C1BD 为等边三角形, ∴∠C1BD=60°, 即异面直线 D1A 与 BD 所成的角为 60°
5 20
24、解:(1)依题意:得 = 0.05, = 0.35, = b,解得 n=100,a=35,b=0.2;
(2)因为第三,四组共有 50 名学生,用分层抽样的方法抽取 5名学生,则第三,四组分别抽取 3名,2 名,
第三组的 3 名学生记为 a1,a2、a3,第四组的 2 名学生记为 b1、b2,则从 5 名学生中随机抽取 2 名,共有
10 种不同取法,具体如下;{a1,a2},(a1,a3},(a1,b1},{a1,b2},{a2,a3},{a2,b1},{a2,b2},{a3,
b1},{a3,b2},{b1,b2},
3
其中全部来自第三组的情况有 3种,具体如下:{a1,a2},{a1,a3},{a2,a3},故所求概率为10
3
25、解:(1)因为 f(x)=2sin(x+ )所以当 sin(x+ )=-l,即 x+ = 2kπ- ,得 x=2kπ一 (k∈Z)时,f(x)
4 4 4 2 4
有最小值一 2:
2 2
(2)由 f(a)= ,得 2sin(a+ )= ,即 sina+cosa = 1 1 8,两边平方,得 1+sin2a = ,所以 sin2a=- .
3 4 3 3 9 9
同课章节目录
