2022.6湖南普通高中学业水平合格性考试数学试卷8(PDF版含答案)
文档属性
| 名称 | 2022.6湖南普通高中学业水平合格性考试数学试卷8(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 09:05:25 | ||
图片预览




文档简介
湖南省 2022年普通高中学业水平合格性考试
数学仿真模拟试卷(八)
本试卷包括选择题、填空题、和解答题三部分。时量 90分钟,满分 100分
一、选择题(本大题共 18 小题,每小题 3 分,满分 54 分。每小题 4 个选项中,只有 1 个选项符合题目要
求,多选不给分)
1.已知集合 A 1,3,5 , B 0,1,2 ,则 A B=( )
A. B. 1 C. {0,1} D. 1, 2,3
2.下列函数中为偶函数的是( )
A. y x B. y x 1 C. y = x2 D. y x3
3.不等式 (x 1)(x 3) 0的解集为( )
A. {x | 1 x 3} B. {x | 3 x 1} C. {x | x 1,或 x 3} D. {x | x 3,或 x 1}
4.命题“ x 1, x2 1”的否定形式是( )
A. x 1, x2 1 B. x 1, x2 1 C. x 1, x2 1 D. x 1, x2 1
5.已知四边形 ABCD 的两条对角线分别为 AC,BD,则“四边形 ABCD 为菱形”是“ AC BD”的( )
A.充分不必要条件 B.充要条件 C.必要不充分条件 D.既不充分也不必要条件
z 2 i6.设 ,则 z 的共轭复数的虚部为( )
1 i
3 1 3 1
A. B. C. D.
2 2 2 2
7.函数 f (x) a x 1(a 0,且 a 1)的图象经过定点( )
A. (0,1) B. (0, 1) C. (0, 2) D. (1,1)
8.一支田径队有男运动员 56 人,女运动员 42 人,若用分层抽样的方法从全体运动员中
抽取一个容量为 28 的样本,则在男运动员中需要抽取的人数为( )
A. 12 B. 14 C. 16 D. 18
9.在平面直角坐标系中,已知角α的终边经过点 (3,4),则 cos ( )
4 3 4 3
A. B. C. D.
3 4 5 5
10.同时掷两个均匀骰子,向上的点数之和是 7 的概率是( )
1 1 1 1
A. B. C. D.
3 4 6 12
11.下列函数中,在 R 上是增函数的是( )
x
A. y lg x B. y log 1 x C. y 1 D. y 10x
2 2
12.已知a (2,m 2),b (4,m),且 a / /b,则 m=( )
A. 4 B. -4 C. 6 D. -6
13.函数 f (x) ln x x 3的零点的个数是( )
A. 0 B.1 C. 2 D.3
14.我国古代数学专著《九章算术》中的“堑堵”是指底面为直角三角形的直棱柱.如图,三棱柱
ABC A1B1C1 为堑堵,其中 AB AC, AB 3, AC 1,则直线 BC 与 A1B1所成角是( )
A. 60° B. 30° C.45° D.150°
15.某人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
A.至多有一次中靶 B.只有一次中靶 C.两次都中靶 D.两次都不中靶
16.如图,在 ABC中,CD 是 AB 边上的中线,点 P是 CD 的中点,则( )
1 1 1 1 1 1 1 1
A. AP AB AC B. AP AB AC C. AP AB AC D. AP AB AC
4 2 2 4 3 2 2 3
x
17.函数 f (x) 4 1 的图象关于( )
2x 1
A.y 轴对称 B.直线 y x对称 C.坐标原点对称 D.直线 y x对称
18.如图,树人中学欲利用原有的墙(墙足够长)为背面,建造一间长方体形状的房屋作为体育器材室.
房屋地面面积为18m2,高度为 3m.若房屋侧面和正面每平方米的造价均为 1000 元,屋顶的造价为
6000 元,且不计房屋背面和地面的费用,则该房屋的最低总造价为( )
A.40000 元 B.42000 元 C.45000 元 D.48000 元
二.填空题(本大题共 4 小题,每小题 4 分,满分 16 分,把答案填在题中的横线上).
19. sin 300 _______.
20.若 f (x 1) x 1 2,则 f 2 ___________.
21. 若函数 f x sin x 3 cos x 在 x 时取得最大值,则 的一个取值为___________.
22.如图,设Ox、Oy是平面内相交成60 角的两条数轴, e y1、 e2 分别是与 x轴、 轴正方向同向的
单位向量.若向量OP xe1 ye2 ,则把有序实数对 x, y 叫做向量OP在斜坐标系 xOy中的坐标,
记作OP x, y.在此斜坐标系 xOy中,已知 a 2,3,b 5,2, a,b夹角为 ,则 ______.
三.解答题(每小题 10 分,共 3 小题,满分 30 分).
23. ABC中的内角 A,B,C所对的边分别为 a,b,c.已知 sin A 3 cos A 0 .
(1)求角 A;(2)若b 4, c 2,求 a.
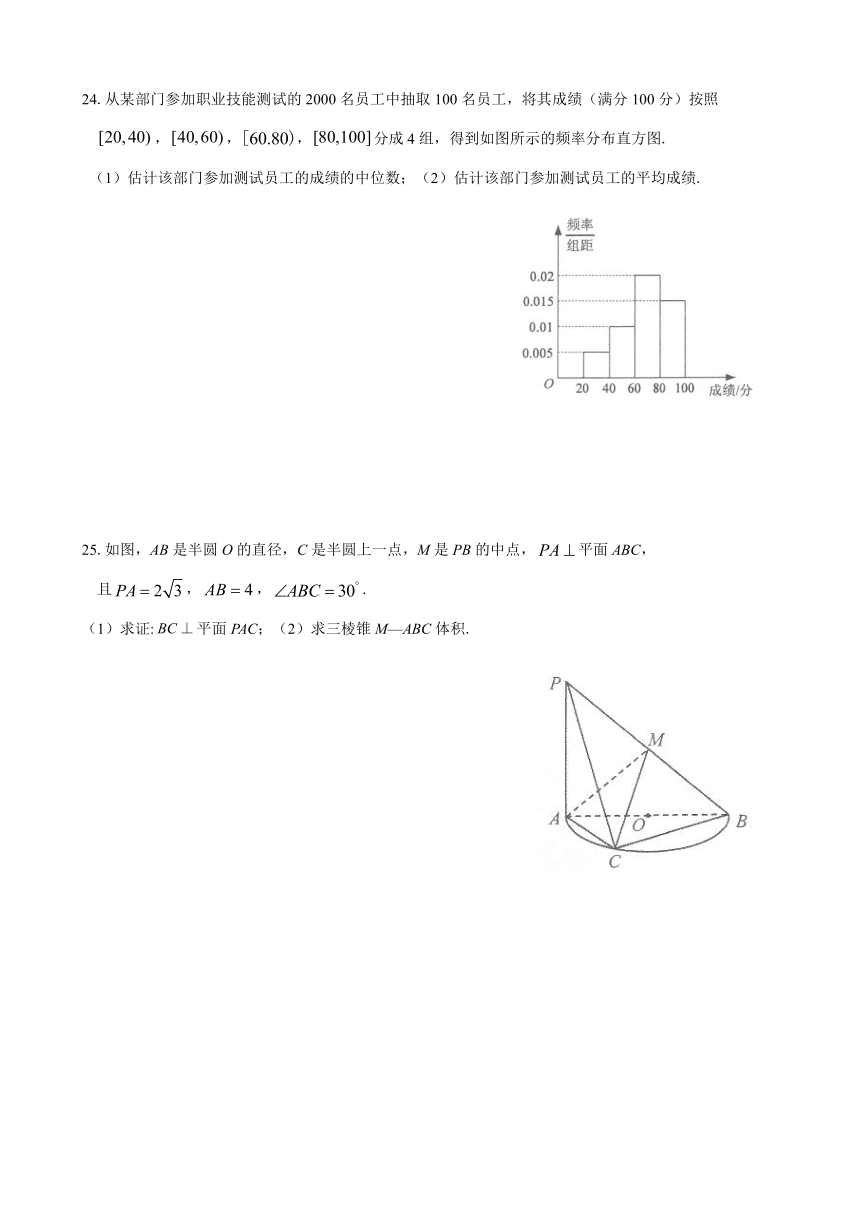
24.从某部门参加职业技能测试的 2000名员工中抽取 100名员工,将其成绩(满分 100分)按照
[20,40),[40,60),[60.80),[80,100]分成 4组,得到如图所示的频率分布直方图.
(1)估计该部门参加测试员工的成绩的中位数;(2)估计该部门参加测试员工的平均成绩.
25.如图,AB是半圆 O的直径,C是半圆上一点,M是 PB的中点, PA 平面 ABC,
且 PA 2 3, AB 4, ABC 30 .
(1)求证: BC⊥平面 PAC;(2)求三棱锥 M—ABC体积.
参考答案
一.选择题
1.解析: A 1,3,5 ,B 0,1,2 , A B 1 ,故选 B
2.解析: y x 定义域为 0, ,不关于原点对称,不是偶函数; y x 1是非奇非偶函数; y = x2是
偶函数, y x3是奇函数;故选:C.
3.解析:因为 (x 1)(x 3) 0,所以 -1< x < 3,即不等式的解集为{x | 1 x 3},故选: A
4.解析: “任意”改为“存在”,否定结论即可. 对“ x 1, x2 1 ”的否定形式是“ x 1, x2 1”.
故选 B
5.解析:若四边形 ABCD为菱形,则 AC BD;反之,若 AC BD,则四边形 ABCD不一定是菱形.故
为充分不必要条件.故选 A.
2 i 2 iz 1 i 1 3i 1 36.解析:因为 i z 1 3 3 ,所以 i,所以 的虚部为 ,故选:1 i 1 i 1 i 2 2 2 2 2 z 2
C
7.解析:因为 f (x) a x 1( a 0,且 a 1),令 x 0,则 f 0 a0 1 2,故函数过点 0,2 ,
故选C
56 4 4
8.解析:由题,男运动员占总体运动员的 ,所以男运动员中需要抽取的人数为 28 16 ,故
56 42 7 7
选:C
x 3
9.解析: x 3,y 4,r 32 42 5, 由任意角的三角函数的定义知,cos ,故选D.r 5
10.解析:同时掷两个均匀骰子,基本事件有6 6 36种,其中点数和为 7 的有 16,25,34,43,52,61 共 6
6 1
种,所以概率为 P .故选:C.
36 6
11.解析:A,B中函数定义域是 (0, ),C,D
1 x
中函数定义域是 R,其中 y ( ) 是减函数, y 10x是增
2
函数.故选:D.
r r
12.解析:因为a (2,m 2),b (4,m),且 a//b,所以 2 m 4 m 2 ,解得m 4故选 A
13.解析:因为 y ln x与 y x 3在 0, 上单调递增,所以 f (x) ln x x 3也在 0, 上单调
递增,又 f 1 ln1 1 3 2 0, f 3 ln3 3 3 ln3 0所以 f 1 f 3 0,故函数在 1,3
上存在唯一零点,故选: B
14.解析:在三棱柱 ABC A1B1C1中,AB//A1B1,所以 ABC为异面直线 A1B1与 BC所成的角,在 ABC
AB AC AC 1 tan ABC AC 1 3中, , AB 3, ,所以 ,所以 ABC 30 ,故异面
AB 3 3
直线 A 1B1与 BC所成的角为30 ,故选 B
15.解析: “至少有一次中靶”与 “至多有一次中靶”均包含中靶一次的情况.故 A 错误.“至少有一次
中靶”与“只有一次中靶” 均包含中靶一次的情况.故 B 错误.“至少有一次中靶”与“两次都中靶”
均包含中靶两次的情况.故C错误.根据互斥事件的定义可得,事件“至少有一次中靶”的互斥事件是“两次都
不中靶”.故选:D
1 1
16.解析:依题意可得 AP AC AD2 , AD AB,2
1 1 1 1 1 所以 AP AC AD AC AB AC AB,故选: A2 2 2 2 4
x 1
17 f (x) 4 1 (2x 2 x ) f (
1
x) (2 x 2x.解析: ,所以 ) f (x),函数为偶函数,图象关于 y
2x 1 2 2
轴对称.故选:A.
xm 18m y 6000 1000 18 18.解析:设房屋的长为 ,则宽为 ,则总造价 3x 2 3x x
36
y 6000 3000 x 36
6000 3000 2 x
36
42000 ,当且仅当 x ,即 x 6时取等号;
x x x
故当长等于6m,宽等于3m时,房屋的最低总造价为 42000元,故选 B
二.填空题(本大题共 4 小题,每小题 4 分,满分 16 分,把答案填在题中的横线上).
1
19、 .
2
20、【解析】因为 f (x 1) x 1 2,所以 f 2 f (1 1) (1 1)2 4,故答案为:4
21. (答案不唯一)
6
f (x) 2 1 sin x 3 cos x 2sin 【解析】因为 x ,
2 2
3
所以当 x 2k , k Z,即 x 2k , k Z时, f (x)取得最大值,
3 2 6
所以 2k , k Z ,所以 可以取 .故答案为: (答案不唯一)
6 6 6
22.【解析】由题, a 2e1 3e2 ,b 5e1 2e2 ,
2 2a b 2e 1 19所以 1 3e2 5e1 2e2 10e1 11e1 e2 6e2 10 11 6 2 2
a 2 2e1 3e2 2
2 2 1
4e1 12e1 e2 9e2 4 12 9 19 ,则 a 19 ,2
2 2 b 2 2 5e1 2e2 25e1 20e1 e2 4e2 25 20 1 4 19 ,则 b 19 ,2
19 2 2
所以 cos a b 2 1 ,则 故答案为: a b 19 19 2 3 3
三.解答题(每小题 10 分,共 3 小题,满分 30 分).
23. ABC中的内角 A,B,C所对的边分别为 a,b,c.已知 sin A 3 cos A 0 .
(1)求角 A;(2)若b 4, c 2,求 a.
【解析】 (1)由 sin A 3 cos A 0,易知cos A 0,则 tan A 3 .因为0 A ,所以 A .3
2 a2 b2 c2( )由余弦定理得 2bc cos A 16 4 2
1
4 2 12,所以
2 a 2 3
.
24.从某部门参加职业技能测试的 2000名员工中抽取 100名员工,将其成绩(满分 100分)按照
[20,40),[40,60),[60.80),[80,100]分成 4组,得到如图所示的频率分布直方图.
(1)估计该部门参加测试员工的成绩的中位数;(2)估计该部门参加测试员工的平均成绩.
【答案】(1)中位数为 70分.(2)平均成绩为 68分.
【解析】(1)设中位数为 x分.因为前 2组频率之和为 0.1 0.2 0.3 0.5,
而前 3组频率之和为 0.1 0.2 0.4 07 0.5,所以60 x 80 .
由0.02(x 60) 0.5 (0.1 0.2) 解得 x 70 .故可估计该部门参加测试员工的成绩的中位数为 70分.
(2)抽取的 100名员工的平均成绩 x 30 0.1 50 0.2 70 0.4 90 0.3 3 10 28 27 68 .
故可估计该部门参加测试员工的平均成绩为 68分.
25.如图,AB是半圆 O的直径,C是半圆上一点,M是 PB的中点, PA 平面 ABC,
且 PA 2 3, AB 4, ABC 30 .
(1)求证: BC⊥平面 PAC;(2)求三棱锥 M—ABC体积.
【解析】(1)证明:因为 AB是半圆O的直径,所以 AC BC .
因为 PA 平面 ABC, BC 平面 ABC,所以 PA BC,
又因为 AC 平面 PAC, PA 平面 PAC,且 AC PA A ,所以 BC⊥平面 PAC .
1
(2)解:因为 ABC 30 , AB 4,所以 BC 2 3, S ABC AB BC sin 30 2 3 .2
连接OM .因为O、M 分别是 AB,PB的中点,所以OM //PA,OM 1 PA 3 .又 PA 平面 ABC .
2
所以OM 平面 ABC 1.因此OM 为三棱锥M ABC的高.所以VM ABC 2 3 3 2 .3
数学仿真模拟试卷(八)
本试卷包括选择题、填空题、和解答题三部分。时量 90分钟,满分 100分
一、选择题(本大题共 18 小题,每小题 3 分,满分 54 分。每小题 4 个选项中,只有 1 个选项符合题目要
求,多选不给分)
1.已知集合 A 1,3,5 , B 0,1,2 ,则 A B=( )
A. B. 1 C. {0,1} D. 1, 2,3
2.下列函数中为偶函数的是( )
A. y x B. y x 1 C. y = x2 D. y x3
3.不等式 (x 1)(x 3) 0的解集为( )
A. {x | 1 x 3} B. {x | 3 x 1} C. {x | x 1,或 x 3} D. {x | x 3,或 x 1}
4.命题“ x 1, x2 1”的否定形式是( )
A. x 1, x2 1 B. x 1, x2 1 C. x 1, x2 1 D. x 1, x2 1
5.已知四边形 ABCD 的两条对角线分别为 AC,BD,则“四边形 ABCD 为菱形”是“ AC BD”的( )
A.充分不必要条件 B.充要条件 C.必要不充分条件 D.既不充分也不必要条件
z 2 i6.设 ,则 z 的共轭复数的虚部为( )
1 i
3 1 3 1
A. B. C. D.
2 2 2 2
7.函数 f (x) a x 1(a 0,且 a 1)的图象经过定点( )
A. (0,1) B. (0, 1) C. (0, 2) D. (1,1)
8.一支田径队有男运动员 56 人,女运动员 42 人,若用分层抽样的方法从全体运动员中
抽取一个容量为 28 的样本,则在男运动员中需要抽取的人数为( )
A. 12 B. 14 C. 16 D. 18
9.在平面直角坐标系中,已知角α的终边经过点 (3,4),则 cos ( )
4 3 4 3
A. B. C. D.
3 4 5 5
10.同时掷两个均匀骰子,向上的点数之和是 7 的概率是( )
1 1 1 1
A. B. C. D.
3 4 6 12
11.下列函数中,在 R 上是增函数的是( )
x
A. y lg x B. y log 1 x C. y 1 D. y 10x
2 2
12.已知a (2,m 2),b (4,m),且 a / /b,则 m=( )
A. 4 B. -4 C. 6 D. -6
13.函数 f (x) ln x x 3的零点的个数是( )
A. 0 B.1 C. 2 D.3
14.我国古代数学专著《九章算术》中的“堑堵”是指底面为直角三角形的直棱柱.如图,三棱柱
ABC A1B1C1 为堑堵,其中 AB AC, AB 3, AC 1,则直线 BC 与 A1B1所成角是( )
A. 60° B. 30° C.45° D.150°
15.某人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
A.至多有一次中靶 B.只有一次中靶 C.两次都中靶 D.两次都不中靶
16.如图,在 ABC中,CD 是 AB 边上的中线,点 P是 CD 的中点,则( )
1 1 1 1 1 1 1 1
A. AP AB AC B. AP AB AC C. AP AB AC D. AP AB AC
4 2 2 4 3 2 2 3
x
17.函数 f (x) 4 1 的图象关于( )
2x 1
A.y 轴对称 B.直线 y x对称 C.坐标原点对称 D.直线 y x对称
18.如图,树人中学欲利用原有的墙(墙足够长)为背面,建造一间长方体形状的房屋作为体育器材室.
房屋地面面积为18m2,高度为 3m.若房屋侧面和正面每平方米的造价均为 1000 元,屋顶的造价为
6000 元,且不计房屋背面和地面的费用,则该房屋的最低总造价为( )
A.40000 元 B.42000 元 C.45000 元 D.48000 元
二.填空题(本大题共 4 小题,每小题 4 分,满分 16 分,把答案填在题中的横线上).
19. sin 300 _______.
20.若 f (x 1) x 1 2,则 f 2 ___________.
21. 若函数 f x sin x 3 cos x 在 x 时取得最大值,则 的一个取值为___________.
22.如图,设Ox、Oy是平面内相交成60 角的两条数轴, e y1、 e2 分别是与 x轴、 轴正方向同向的
单位向量.若向量OP xe1 ye2 ,则把有序实数对 x, y 叫做向量OP在斜坐标系 xOy中的坐标,
记作OP x, y.在此斜坐标系 xOy中,已知 a 2,3,b 5,2, a,b夹角为 ,则 ______.
三.解答题(每小题 10 分,共 3 小题,满分 30 分).
23. ABC中的内角 A,B,C所对的边分别为 a,b,c.已知 sin A 3 cos A 0 .
(1)求角 A;(2)若b 4, c 2,求 a.
24.从某部门参加职业技能测试的 2000名员工中抽取 100名员工,将其成绩(满分 100分)按照
[20,40),[40,60),[60.80),[80,100]分成 4组,得到如图所示的频率分布直方图.
(1)估计该部门参加测试员工的成绩的中位数;(2)估计该部门参加测试员工的平均成绩.
25.如图,AB是半圆 O的直径,C是半圆上一点,M是 PB的中点, PA 平面 ABC,
且 PA 2 3, AB 4, ABC 30 .
(1)求证: BC⊥平面 PAC;(2)求三棱锥 M—ABC体积.
参考答案
一.选择题
1.解析: A 1,3,5 ,B 0,1,2 , A B 1 ,故选 B
2.解析: y x 定义域为 0, ,不关于原点对称,不是偶函数; y x 1是非奇非偶函数; y = x2是
偶函数, y x3是奇函数;故选:C.
3.解析:因为 (x 1)(x 3) 0,所以 -1< x < 3,即不等式的解集为{x | 1 x 3},故选: A
4.解析: “任意”改为“存在”,否定结论即可. 对“ x 1, x2 1 ”的否定形式是“ x 1, x2 1”.
故选 B
5.解析:若四边形 ABCD为菱形,则 AC BD;反之,若 AC BD,则四边形 ABCD不一定是菱形.故
为充分不必要条件.故选 A.
2 i 2 iz 1 i 1 3i 1 36.解析:因为 i z 1 3 3 ,所以 i,所以 的虚部为 ,故选:1 i 1 i 1 i 2 2 2 2 2 z 2
C
7.解析:因为 f (x) a x 1( a 0,且 a 1),令 x 0,则 f 0 a0 1 2,故函数过点 0,2 ,
故选C
56 4 4
8.解析:由题,男运动员占总体运动员的 ,所以男运动员中需要抽取的人数为 28 16 ,故
56 42 7 7
选:C
x 3
9.解析: x 3,y 4,r 32 42 5, 由任意角的三角函数的定义知,cos ,故选D.r 5
10.解析:同时掷两个均匀骰子,基本事件有6 6 36种,其中点数和为 7 的有 16,25,34,43,52,61 共 6
6 1
种,所以概率为 P .故选:C.
36 6
11.解析:A,B中函数定义域是 (0, ),C,D
1 x
中函数定义域是 R,其中 y ( ) 是减函数, y 10x是增
2
函数.故选:D.
r r
12.解析:因为a (2,m 2),b (4,m),且 a//b,所以 2 m 4 m 2 ,解得m 4故选 A
13.解析:因为 y ln x与 y x 3在 0, 上单调递增,所以 f (x) ln x x 3也在 0, 上单调
递增,又 f 1 ln1 1 3 2 0, f 3 ln3 3 3 ln3 0所以 f 1 f 3 0,故函数在 1,3
上存在唯一零点,故选: B
14.解析:在三棱柱 ABC A1B1C1中,AB//A1B1,所以 ABC为异面直线 A1B1与 BC所成的角,在 ABC
AB AC AC 1 tan ABC AC 1 3中, , AB 3, ,所以 ,所以 ABC 30 ,故异面
AB 3 3
直线 A 1B1与 BC所成的角为30 ,故选 B
15.解析: “至少有一次中靶”与 “至多有一次中靶”均包含中靶一次的情况.故 A 错误.“至少有一次
中靶”与“只有一次中靶” 均包含中靶一次的情况.故 B 错误.“至少有一次中靶”与“两次都中靶”
均包含中靶两次的情况.故C错误.根据互斥事件的定义可得,事件“至少有一次中靶”的互斥事件是“两次都
不中靶”.故选:D
1 1
16.解析:依题意可得 AP AC AD2 , AD AB,2
1 1 1 1 1 所以 AP AC AD AC AB AC AB,故选: A2 2 2 2 4
x 1
17 f (x) 4 1 (2x 2 x ) f (
1
x) (2 x 2x.解析: ,所以 ) f (x),函数为偶函数,图象关于 y
2x 1 2 2
轴对称.故选:A.
xm 18m y 6000 1000 18 18.解析:设房屋的长为 ,则宽为 ,则总造价 3x 2 3x x
36
y 6000 3000 x 36
6000 3000 2 x
36
42000 ,当且仅当 x ,即 x 6时取等号;
x x x
故当长等于6m,宽等于3m时,房屋的最低总造价为 42000元,故选 B
二.填空题(本大题共 4 小题,每小题 4 分,满分 16 分,把答案填在题中的横线上).
1
19、 .
2
20、【解析】因为 f (x 1) x 1 2,所以 f 2 f (1 1) (1 1)2 4,故答案为:4
21. (答案不唯一)
6
f (x) 2 1 sin x 3 cos x 2sin 【解析】因为 x ,
2 2
3
所以当 x 2k , k Z,即 x 2k , k Z时, f (x)取得最大值,
3 2 6
所以 2k , k Z ,所以 可以取 .故答案为: (答案不唯一)
6 6 6
22.【解析】由题, a 2e1 3e2 ,b 5e1 2e2 ,
2 2a b 2e 1 19所以 1 3e2 5e1 2e2 10e1 11e1 e2 6e2 10 11 6 2 2
a 2 2e1 3e2 2
2 2 1
4e1 12e1 e2 9e2 4 12 9 19 ,则 a 19 ,2
2 2 b 2 2 5e1 2e2 25e1 20e1 e2 4e2 25 20 1 4 19 ,则 b 19 ,2
19 2 2
所以 cos a b 2 1 ,则 故答案为: a b 19 19 2 3 3
三.解答题(每小题 10 分,共 3 小题,满分 30 分).
23. ABC中的内角 A,B,C所对的边分别为 a,b,c.已知 sin A 3 cos A 0 .
(1)求角 A;(2)若b 4, c 2,求 a.
【解析】 (1)由 sin A 3 cos A 0,易知cos A 0,则 tan A 3 .因为0 A ,所以 A .3
2 a2 b2 c2( )由余弦定理得 2bc cos A 16 4 2
1
4 2 12,所以
2 a 2 3
.
24.从某部门参加职业技能测试的 2000名员工中抽取 100名员工,将其成绩(满分 100分)按照
[20,40),[40,60),[60.80),[80,100]分成 4组,得到如图所示的频率分布直方图.
(1)估计该部门参加测试员工的成绩的中位数;(2)估计该部门参加测试员工的平均成绩.
【答案】(1)中位数为 70分.(2)平均成绩为 68分.
【解析】(1)设中位数为 x分.因为前 2组频率之和为 0.1 0.2 0.3 0.5,
而前 3组频率之和为 0.1 0.2 0.4 07 0.5,所以60 x 80 .
由0.02(x 60) 0.5 (0.1 0.2) 解得 x 70 .故可估计该部门参加测试员工的成绩的中位数为 70分.
(2)抽取的 100名员工的平均成绩 x 30 0.1 50 0.2 70 0.4 90 0.3 3 10 28 27 68 .
故可估计该部门参加测试员工的平均成绩为 68分.
25.如图,AB是半圆 O的直径,C是半圆上一点,M是 PB的中点, PA 平面 ABC,
且 PA 2 3, AB 4, ABC 30 .
(1)求证: BC⊥平面 PAC;(2)求三棱锥 M—ABC体积.
【解析】(1)证明:因为 AB是半圆O的直径,所以 AC BC .
因为 PA 平面 ABC, BC 平面 ABC,所以 PA BC,
又因为 AC 平面 PAC, PA 平面 PAC,且 AC PA A ,所以 BC⊥平面 PAC .
1
(2)解:因为 ABC 30 , AB 4,所以 BC 2 3, S ABC AB BC sin 30 2 3 .2
连接OM .因为O、M 分别是 AB,PB的中点,所以OM //PA,OM 1 PA 3 .又 PA 平面 ABC .
2
所以OM 平面 ABC 1.因此OM 为三棱锥M ABC的高.所以VM ABC 2 3 3 2 .3
同课章节目录
