2.2 探索直线平行的条件(第二课时)学案
文档属性
| 名称 | 2.2 探索直线平行的条件(第二课时)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 53.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-05 00:00:00 | ||
图片预览


文档简介
初 一 年级 数学 学科导学案
复备人所在单位 上课时间 4.3
复备人 课型 新授课 复备时间 4.2 课时 1
课 题 2.2 探索直线平行的条件(2)
教
学
目
标 知识能力 1.会识别由“三线八角”构成的内错角合同旁内角。2.经历探索直线平行条件的过程,掌握利用同位角相等、同旁内角互补判别直线平行的结论,并能解决一些问题。
过程方法 经历观察、操作、想象、图利、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
情感态度价值观 进一步体验数学与实际生活的密切联系。
学 习 重 点 弄清内错角和同旁内角的意义,会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。
学 习 难 点 会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”
教学、教具
(课件)
准 备 多媒体教学,课件
教法、学法 自主合作探究
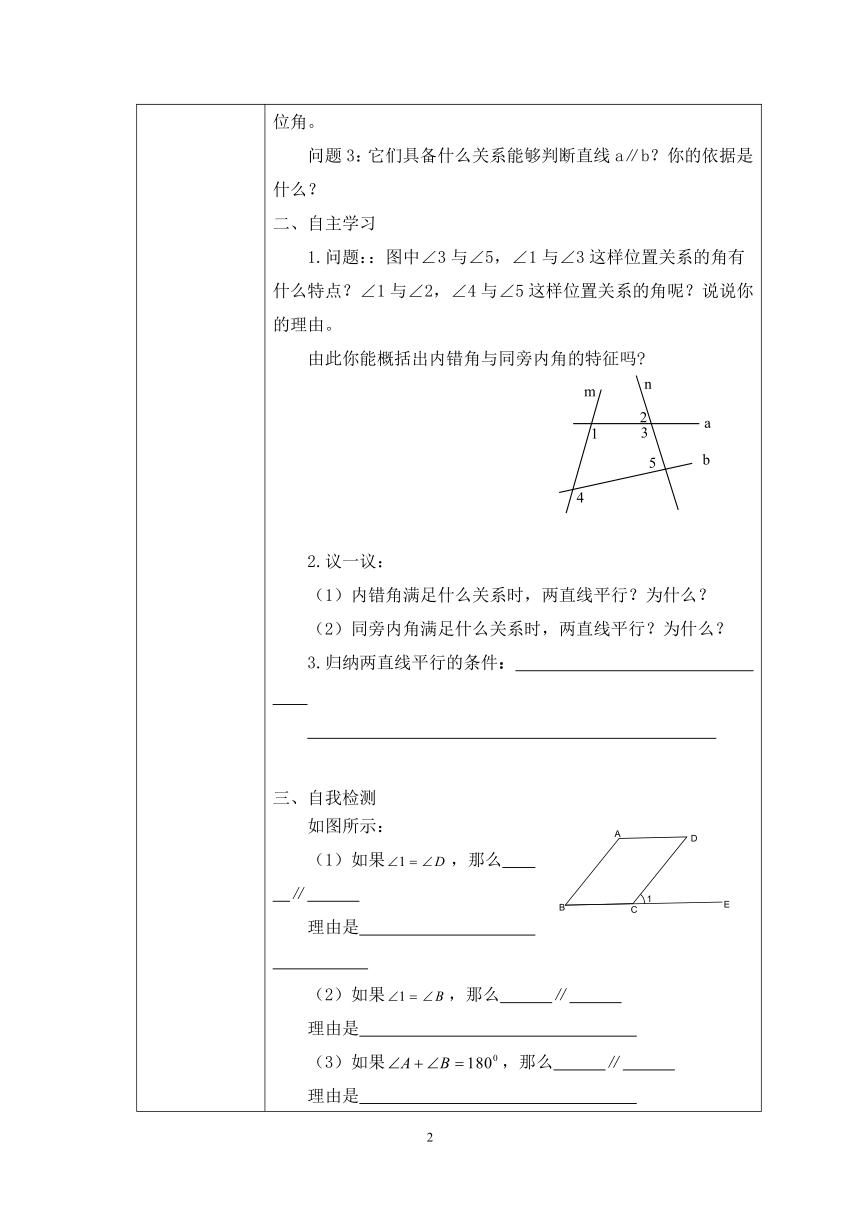
自主学习 一、复习旧知问题1:如图,直线a,b被直线c所截,数一数图中有几个角(不含平角)?问题2:写出图中的所有同位角,并用自己的语言说明什么样的角是同位角?引导学生从角与截线与被截线的位置关系的角度来描述同位角。问题3:它们具备什么关系能够判断直线a∥b?你的依据是什么?二、自主学习1.问题::图中∠3与∠5,∠1与∠3这样位置关系的角有什么特点?∠1与∠2,∠4与∠5这样位置关系的角呢?说说你的理由。由此你能概括出内错角与同旁内角的特征吗 2.议一议:(1)内错角满足什么关系时,两直线平行?为什么?(2)同旁内角满足什么关系时,两直线平行?为什么?3.归纳两直线平行的条件: 三、自我检测如图所示:(1)如果,那么 ∥ 理由是 (2)如果,那么 ∥ 理由是 (3)如果,那么 ∥ 理由是 (4)如果,那么 ∥ 理由是
自我评价:我得了( )颗★ 小组长评价:你得了( )颗★
合作探究 1.同位角、内错角、同旁内角的特征(简称“三线八角”)如下表:基本图形角的名称位置特征图形结构特征2.平行判定2:两条直线被第三条直线所截,如果内错角 ,那么这两直线 。简称: 如图,可表述为:∵ ( ) ∴ ( )平行判定3:两条直线被第三条直线所截,如果同旁内角 ,那么这两直线 。简称: 如图,可表述为:∵ ( )∴ ( )例1、如右图,∵∠1=∠2 ∴ ∥ ,( )∵∠2= ∴ ∥ ,(同位角相等,两直线平行)∵∠3+∠4=180°∴ ∥ , ∴AC∥FG, 变式训练:如图所示,AB⊥BC于点B,BC⊥CD于点C,∠1=∠2,那么EB∥CF吗?为什么?例2、如图,已知,那么AB∥CD成立吗?请说明理由。变式训练:如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?解:因为∠1+∠2=180°( )所以AB∥_______( )又因为∠1=∠3( )所以∠2+∠________=180°( )所以EF∥GH( )拓展:1、如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.解:AB∥CD 理由如下:∵BE是∠ABD的平分线,DE是∠BDC的平分线( )∴∠1= ,∠2= ( )∵∠1+∠2=90 ( )∴∠ABD+∠CDB= = =180 ∴CD∥AB( )2.如图所示,根据下列条件可推得哪两条直线平行,并说明理由。(1)∠ABD=∠CDB;(2)∠CBA+∠BAD=180 ;(3)∠CAD=∠ACB。
形成
结论 内错角相等,两直线平行。 同旁内角互补,两直线平行。
小组长评价:你得了( )颗★
精讲点拨 具备同位角关系的一对角是在被截直线的同一侧,在截线的同一旁,相对位置是相同的,在两条被截直线的内部,在截线的两侧,位置是交错的,这样的角叫做内错角;在两条被截直线的内部,在截线的同旁,这样的角叫做同旁内角.
课堂小结 通过本节课的学习,你收获了什么
达标检测 1.下列结论中,不正确的是( )A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行。B.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。C.两条直线被第三条直线所截,那么这两条直线平行。D.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。2.两条直线被第三条直线所截,下列条件不能判定这两条直线平行的是( )A.同位角相等 B.内错角相等 C.同旁内角互补 D.同旁内角相等3.如图① 不能判定∥的一组条件是( )A.∠1=∠2 B.∠1=∠5 C.∠3=∠4 D.∠2=∠64.如图② 能够判定DE∥BC的条件是( )A. ∠DCE+∠DEC= B. ∠EDC=∠DCB C. ∠BGF=∠DCB D. CD⊥AB,GF⊥AB5.如图5所示AE∥BD,下列说法不正确的是( )A.∠1=∠2 B.∠A=∠CBD C.∠BDE+∠DEA=180° D.∠3=∠4 图5 图6 图76.如图6所示,能说明AB∥DE的有( ) ①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.A.1个 B.2个 C.3个 D.4个7.如图7所示,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5 8.如图1所示,若∠BEF+______=180°,则AB∥CD.9.如图2所示,请你写一个适当的条件_______, 使AD∥BC. 图2 图3 10.如图3所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
教师评价:你得了( )颗★
板书设计 2.2 探索直线平行的条件(2)内错角相等,两直线平行。 同旁内角互补,两直线平行。
课后反思
c
a
b
a
n
m
b
3
4
5
2
1
1
复备人所在单位 上课时间 4.3
复备人 课型 新授课 复备时间 4.2 课时 1
课 题 2.2 探索直线平行的条件(2)
教
学
目
标 知识能力 1.会识别由“三线八角”构成的内错角合同旁内角。2.经历探索直线平行条件的过程,掌握利用同位角相等、同旁内角互补判别直线平行的结论,并能解决一些问题。
过程方法 经历观察、操作、想象、图利、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
情感态度价值观 进一步体验数学与实际生活的密切联系。
学 习 重 点 弄清内错角和同旁内角的意义,会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。
学 习 难 点 会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”
教学、教具
(课件)
准 备 多媒体教学,课件
教法、学法 自主合作探究
自主学习 一、复习旧知问题1:如图,直线a,b被直线c所截,数一数图中有几个角(不含平角)?问题2:写出图中的所有同位角,并用自己的语言说明什么样的角是同位角?引导学生从角与截线与被截线的位置关系的角度来描述同位角。问题3:它们具备什么关系能够判断直线a∥b?你的依据是什么?二、自主学习1.问题::图中∠3与∠5,∠1与∠3这样位置关系的角有什么特点?∠1与∠2,∠4与∠5这样位置关系的角呢?说说你的理由。由此你能概括出内错角与同旁内角的特征吗 2.议一议:(1)内错角满足什么关系时,两直线平行?为什么?(2)同旁内角满足什么关系时,两直线平行?为什么?3.归纳两直线平行的条件: 三、自我检测如图所示:(1)如果,那么 ∥ 理由是 (2)如果,那么 ∥ 理由是 (3)如果,那么 ∥ 理由是 (4)如果,那么 ∥ 理由是
自我评价:我得了( )颗★ 小组长评价:你得了( )颗★
合作探究 1.同位角、内错角、同旁内角的特征(简称“三线八角”)如下表:基本图形角的名称位置特征图形结构特征2.平行判定2:两条直线被第三条直线所截,如果内错角 ,那么这两直线 。简称: 如图,可表述为:∵ ( ) ∴ ( )平行判定3:两条直线被第三条直线所截,如果同旁内角 ,那么这两直线 。简称: 如图,可表述为:∵ ( )∴ ( )例1、如右图,∵∠1=∠2 ∴ ∥ ,( )∵∠2= ∴ ∥ ,(同位角相等,两直线平行)∵∠3+∠4=180°∴ ∥ , ∴AC∥FG, 变式训练:如图所示,AB⊥BC于点B,BC⊥CD于点C,∠1=∠2,那么EB∥CF吗?为什么?例2、如图,已知,那么AB∥CD成立吗?请说明理由。变式训练:如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?解:因为∠1+∠2=180°( )所以AB∥_______( )又因为∠1=∠3( )所以∠2+∠________=180°( )所以EF∥GH( )拓展:1、如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.解:AB∥CD 理由如下:∵BE是∠ABD的平分线,DE是∠BDC的平分线( )∴∠1= ,∠2= ( )∵∠1+∠2=90 ( )∴∠ABD+∠CDB= = =180 ∴CD∥AB( )2.如图所示,根据下列条件可推得哪两条直线平行,并说明理由。(1)∠ABD=∠CDB;(2)∠CBA+∠BAD=180 ;(3)∠CAD=∠ACB。
形成
结论 内错角相等,两直线平行。 同旁内角互补,两直线平行。
小组长评价:你得了( )颗★
精讲点拨 具备同位角关系的一对角是在被截直线的同一侧,在截线的同一旁,相对位置是相同的,在两条被截直线的内部,在截线的两侧,位置是交错的,这样的角叫做内错角;在两条被截直线的内部,在截线的同旁,这样的角叫做同旁内角.
课堂小结 通过本节课的学习,你收获了什么
达标检测 1.下列结论中,不正确的是( )A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行。B.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。C.两条直线被第三条直线所截,那么这两条直线平行。D.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。2.两条直线被第三条直线所截,下列条件不能判定这两条直线平行的是( )A.同位角相等 B.内错角相等 C.同旁内角互补 D.同旁内角相等3.如图① 不能判定∥的一组条件是( )A.∠1=∠2 B.∠1=∠5 C.∠3=∠4 D.∠2=∠64.如图② 能够判定DE∥BC的条件是( )A. ∠DCE+∠DEC= B. ∠EDC=∠DCB C. ∠BGF=∠DCB D. CD⊥AB,GF⊥AB5.如图5所示AE∥BD,下列说法不正确的是( )A.∠1=∠2 B.∠A=∠CBD C.∠BDE+∠DEA=180° D.∠3=∠4 图5 图6 图76.如图6所示,能说明AB∥DE的有( ) ①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.A.1个 B.2个 C.3个 D.4个7.如图7所示,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5 8.如图1所示,若∠BEF+______=180°,则AB∥CD.9.如图2所示,请你写一个适当的条件_______, 使AD∥BC. 图2 图3 10.如图3所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
教师评价:你得了( )颗★
板书设计 2.2 探索直线平行的条件(2)内错角相等,两直线平行。 同旁内角互补,两直线平行。
课后反思
c
a
b
a
n
m
b
3
4
5
2
1
1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
