北师大初中数学七下第二章平行线与相交线全章学案(共8课时)
文档属性
| 名称 | 北师大初中数学七下第二章平行线与相交线全章学案(共8课时) |  | |
| 格式 | zip | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-05 23:14:16 | ||
图片预览

文档简介
2.1 两条直线的位置关系(1)
一、学习目标:
1、知识目标:在具体情景中了解对顶角、补角、余角,知道对顶角相等、同角或等角的余角相等、同角等角的补角相等,并能解决一些实际问题。
2、能力目标:(1)经历观察、操作、推理、交流等过程,发展空间观念、推理能力和有条理地表达的能力。(2)能运用互为余角、互为补角、对顶角等相关的知识解决一些实际问题。
3、情感目标:在活动中培养学生乐于探究、合作的习惯,体验探索成功、感受创新的乐趣,从而培养学习数学的主动性;进一步体会“数学就在我们身边”,增强学生用数学解决实际问题的意识。
二、学习重点:了解补角、余角、对顶角,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等。
三、学习难点:学生探索同角或等角的余角相等、同角或等角的补角相等、对顶角相等的过程以及对其意义的理解,并能解决一些实际问题。初步的“说理”也是难点之一。
四、学习设计:
(一)预习准备:预习书38、39页,回答下列问题:
(1)在 内,两条直线的位置关系有 和 两种。
(2)若两条直线 ,我们称这两条直线为相交线。
(3)在 内,不相交的两条直线叫 。
(4)下列图形中是对顶角的有 个。
(5)预习作业:
①已知∠1=36°,∠2=54°,那么∠1+∠2=_________
②已知∠1=144°,∠2=36°,那么∠1+∠2=_________
(二)学习过程:
1、创设情境,引入课题
完成书P38议一议,填空:
(1)对顶角具有的特点是①
② 。
(2)对顶角的性质是 。
2、展示新知:
完成书P39想一想,填空:
⑴如果两个角的和等于 ,我们就说这两个角互为余角,简称互余;如果两个角的和等于 ,就说这两个角互为补角,简称互补。
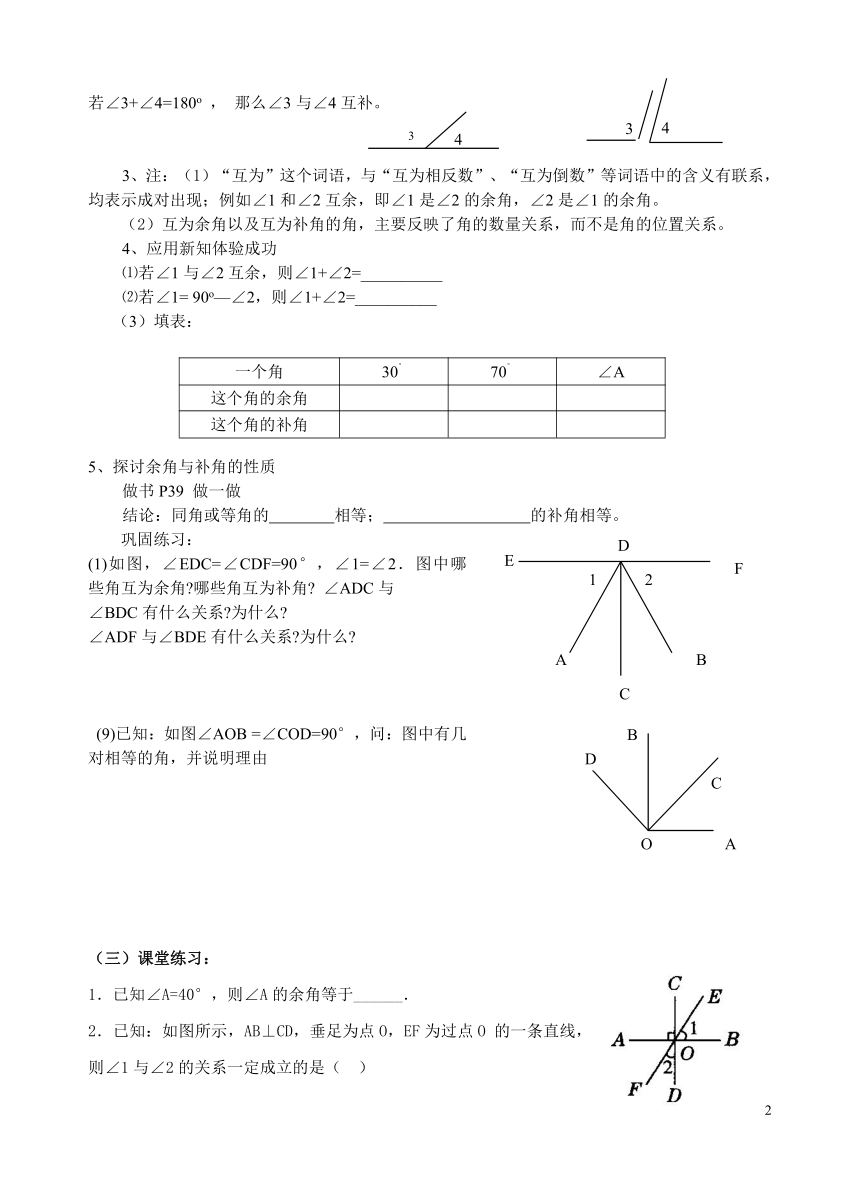
⑵符号语言:若∠1+∠2= 90o , 那么∠1与∠2互余。
若∠3+∠4=180o , 那么∠3与∠4互补。
3、注:(1)“互为”这个词语,与“互为相反数”、“互为倒数”等词语中的含义有联系,均表示成对出现;例如∠1和∠2互余,即∠1是∠2的余角,∠2是∠1的余角。
(2)互为余角以及互为补角的角,主要反映了角的数量关系,而不是角的位置关系。
4、应用新知体验成功
⑴若∠1与∠2互余,则∠1+∠2=__________
⑵若∠1= 90o—∠2,则∠1+∠2=__________
(3)填表:
一个角 30° 70° ∠A
这个角的余角
这个角的补角
5、探讨余角与补角的性质
做书P39 做一做
结论:同角或等角的 相等; 的补角相等。
巩固练习:
(1)如图,∠EDC=∠CDF=90°,∠1=∠2.图中哪 些角互为余角 哪些角互为补角 ∠ADC与
∠BDC有什么关系 为什么
∠ADF与∠BDE有什么关系 为什么
(9)已知:如图∠AOB =∠COD=90°,问:图中有几对相等的角,并说明理由
(三)课堂练习:
1.已知∠A=40°,则∠A的余角等于______.
2.已知:如图所示,AB⊥CD,垂足为点O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.互为对顶角
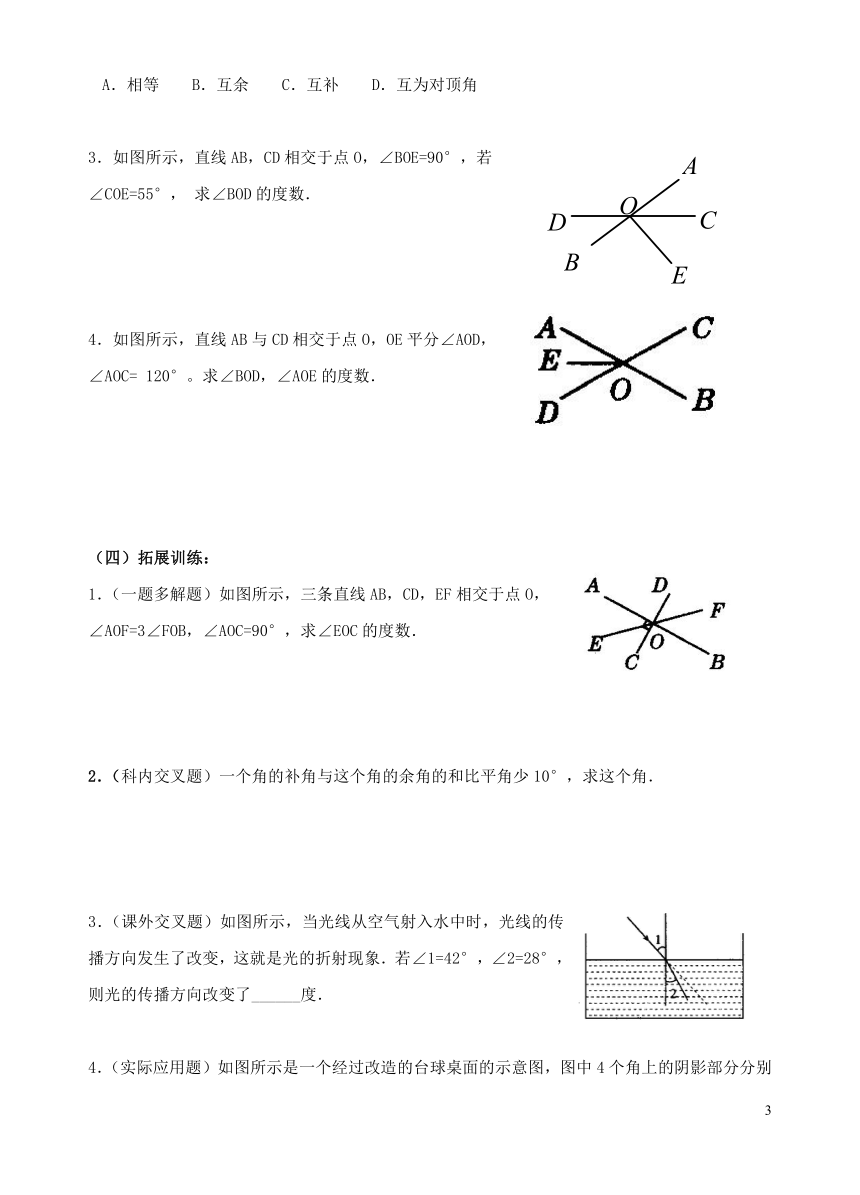
3.如图所示,直线AB,CD相交于点O,∠BOE=90°,若
∠COE=55°,求∠BOD的度数.
4.如图所示,直线AB与CD相交于点O,OE平分∠AOD,
∠AOC=120°。求∠BOD,∠AOE的度数.
(四)拓展训练:
1.(一题多解题)如图所示,三条直线AB,CD,EF相交于点O,
∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数.
2.(科内交叉题)一个角的补角与这个角的余角的和比平角少10°,求这个角.
3.(课外交叉题)如图所示,当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象.若∠1=42°,∠2=28°,则光的传播方向改变了______度.
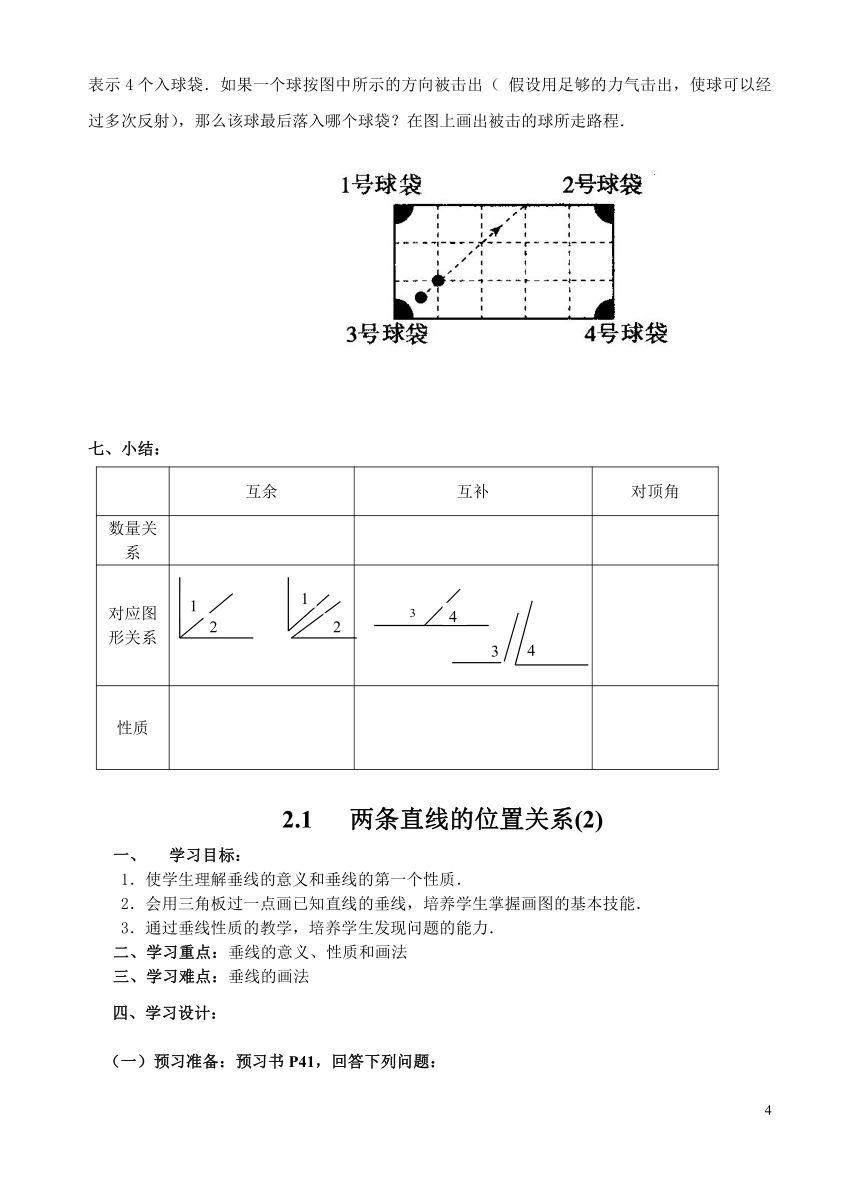
4.(实际应用题)如图所示是一个经过改造的台球桌面的示意图,图中4个角上的阴影部分分别表示4个入球袋.如果一个球按图中所示的方向被击出(假设用足够的力气击出,使球可以经过多次反射),那么该球最后落入哪个球袋?在图上画出被击的球所走路程.
七、小结:
互余 互补 对顶角
数量关系
对应图形关系
性质
两条直线的位置关系(2)
学习目标:
1.使学生理解垂线的意义和垂线的第一个性质.
2.会用三角板过一点画已知直线的垂线,培养学生掌握画图的基本技能.
3.通过垂线性质的教学,培养学生发现问题的能力.
二、学习重点:垂线的意义、性质和画法
三、学习难点:垂线的画法
四、学习设计:
(一)预习准备:预习书P41,回答下列问题:
(1) 在平面内的两条直线有 和 两种位置关系,而垂直是 位置关系中的一种特殊情况。
(2) ,那么称这两条直线互相垂直,其中一条直线叫做另一条直线的 ,它们的交点叫 .
(3)通常用符号 表示两条直线互相垂直,“⊥”读作“垂直于”,如AB⊥CD于M,含义是直线AB与直线CD垂直,垂足是M。
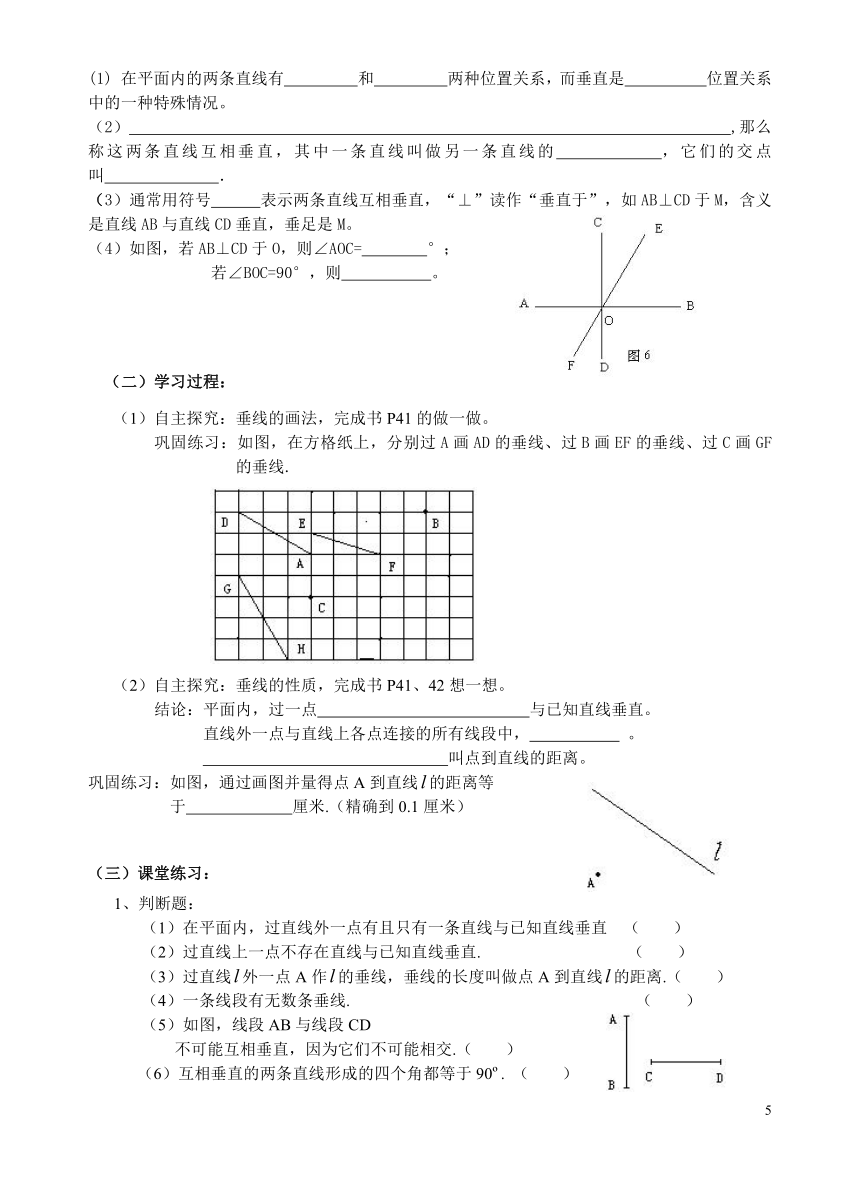
(4)如图,若AB⊥CD于O,则∠AOC= °;
若∠BOC=90°,则 。
(二)学习过程:
(1)自主探究:垂线的画法,完成书P41的做一做。
巩固练习:如图,在方格纸上,分别过A画AD的垂线、过B画EF的垂线、过C画GF的垂线.
(2)自主探究:垂线的性质,完成书P41、42想一想。
结论:平面内,过一点 与已知直线垂直。
直线外一点与直线上各点连接的所有线段中, 。
叫点到直线的距离。
巩固练习:如图,通过画图并量得点A到直线的距离等
于 厘米.(精确到0.1厘米)
(三)课堂练习:
1、判断题:
(1)在平面内,过直线外一点有且只有一条直线与已知直线垂直 ( )
(2)过直线上一点不存在直线与已知直线垂直. ( )
(3)过直线外一点A作的垂线,垂线的长度叫做点A到直线的距离.( )
(4)一条线段有无数条垂线. ( )
(5)如图,线段AB与线段CD
不可能互相垂直,因为它们不可能相交.( )
(6)互相垂直的两条直线形成的四个角都等于90 . ( )
2、下列说法错误的个数是( )
一条直线的垂线只有一条;②一条直线的垂线有无数条;
③过一点画一条直线的垂线只能画一条
A、0 B、1 C、2 D、3
3、如果两条直线相交成( ),那么这两条直线互相垂直
A、锐角 B、直角 C、钝角 D、任意一个角
4、过一条线段外一点画这条线段的垂线,垂足在( )
A、这条线段上 B、这条线段的端点上
C、这条线段的延长线上 D、以上都有可能
5、在一个平面内过直线上一点A画的平行线,能画出 条;过直线上一点A画的垂线,能画出 条.
6、在下列各图中,用三角板分别过点C画线段AB的垂线.
(1) (2) (3) (4)
7、将一张长方形纸对折,使OA与OB重合,这时∠AOC是什么角?为什么?
(四)拓展训练:
1、按照题目的要求,分别画出图形,并回答有关问题.
画长3cm的线段AB,取AB的中点O,过O作线段AB的垂线,在上任取一点P,连接PA,PB,量一量线段PA,PB的长度,你发现什么结论?
画一个∠ABC,作出∠ABC的角平分线BD,在BD上任取一点P(除B点外),过P分别作PM⊥BA,PN⊥BC,垂足分别是M,N,量一量线段PM,PN的长度,你发现什么结论?
2、按题目要求画图,并回答相关问题.
画两条直线m,n,使m∥n,在直线m上任取两点A,B,分别过A,B作直线n的垂线,垂足分别为C,D,量一量线段AC,BD的长,你发现了什么结论?
如图,点P是∠AOB内一点,过点P作PM⊥OA,
垂足为M,作PN⊥OB,垂足为N,量一量∠MPN
和∠O,你发现了什么结论?
2.2 探索直线平行的条件(1)
一、学习目标:
1、经历观察、操作、想象、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达的能力。
2、会认由三线八角所成的同位角。
3、掌握平行线公理及平行线的传递性。
4、掌握直线平行的条件并能解决一些问题
二、学习重点:会认各种图形下的同位角,并掌握直线平行的条件是“同位角相等,两直线平行”
三、学习难点:判断两直线平行的说理过程
四、学习设计:
(一)课前准备
(1)预习书44-48页
(2) 思考①什么叫同位角、内错角、同旁内角?②同位角、内错角、同旁内角有什么特征?
(3)预习作业
如图所示,①是 角;它们是由直线 和直线 ,被直线 所截得的;②是 角;它们是由直线 和直线 ,被直线 所截得的;③是 角;它们是由直线 和直线 ,被直线 所截得的。
(二)学习过程
1、两直线被第三直线所截,可形成的角有 , , 。
例1如图是同位角关系的两角是 ,是互补关系的两角是 ,是对顶角的是 。
2、平行判定1:两条直线被第三条直线所截,如果同位角 ,那么这两直线 。
简称: (公理)
如图,可表述为:
∵ ( )
∴ ( )
如图
(1)
(垂直的定义)
∴ ∥ (同位角相等,两直线平行)
(2)用一句精炼的话总结(1)所包含的规律
变式训练:如图所示
1、(已知)
∴ ∥ ( )
2、(已知)
∴ ∥ ( )
例3、如图,已知,直线BC与DF平行吗?为什么?
变式训练:如图,已知,试问a与b平行吗?说说你的理由。
过已知直线a外一点p画a的平行线b
P .
a
平行线公理:过直线外一点有 条直线与这条直线平行。
平行线的传递性:
几何语言:
拓展:
如图,已知,问再添加什么条件可使AB∥CD?试说明理由。
2.2 探索直线平行的条件(2)
一、学习目标:
1、经历观察、操作、想象、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
2、经历探索直线平行的条件的过程,掌握直线平行的条件,并能解决一些问题。
3、会用三角尺过已知直线外一点画这条直线的平行线。
二、学习重点:弄清内错角和同旁内角的意义,会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。
三、学习难点:
会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。
四、学习设计
(一)预习准备
(1)预习书47-48页
(2)回顾:①什么是同位角?什么是内错角?什么是同旁内角?
同位角、内错角、同旁内角的特征(简称“三线八角”)如下表:
基本图形 角的名称 位置特征 图形结构特征
②同位角相等,两直线平行。
(3)预习作业:
如图所示:
(1)如果,那么 ∥
理由是
(2)如果,那么 ∥
理由是
(3)如果,那么 ∥
理由是
(4)如果,那么 ∥
理由是
(二)新课学行判定2:两条直线被第三条直线所截,如果内错角 ,那么这两直线 。
简称:
如图,可表述为:
∵ ( )
∴ ( )
平行判定3:两条直线被第三条直线所截,如果同旁内角 ,那么这两直线 。
简称:
如图,可表述为:
∵ ( )
∴ ( )
例1、如右图,∵∠1=∠2
∴ ∥ ,
∵∠2=
∴ ∥ ,(同位角相等,两直线平行)
∵∠3+∠4=180°
∴ ∥ ,
∴AC∥FG,
变式训练:如图所示,AB⊥BC于点B,BC⊥CD于点C,∠1=∠2,那么EB∥CF吗?为什么?
例2、如图,已知,那么AB∥CD成立吗?请说明理由。
变式训练:如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?
解:为∠1+∠2=180°( )
所以AB∥_______( )
又因为∠1=∠3( )
所以∠2+∠________=180°( )
所以EF∥GH( )
拓展:1、如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
解:AB∥CD 理由如下:
∵BE是∠ABD的平分线,DE是∠BDC的平分线( )
∴∠1= ,∠2= ( )
∵∠1+∠2=90 ( )
∴∠ABD+∠CDB= = =180 。
∴CD∥AB( )
2.如图所示,根据下列条件可推得哪两条直线平行,并说明理由。
(1)∠ABD=∠CDB;(2)∠CBA+∠BAD=180 ;
(3)∠CAD=∠ACB。
当堂测评:
1.下列结论中,不正确的是( )
A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
B.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
C.两条直线被第三条直线所截,那么这两条直线平行。
D.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
2.两条直线被第三条直线所截,下列条件不能判定这两条直线平行的是( )
A.同位角相等 B.内错角相等 C.同旁内角互补 D.同旁内角相等
3.如图① 不能判定∥的一组条件是( )
A.∠1=∠2 B.∠1=∠5 C.∠3=∠4 D.∠2=∠6
4.如图② 能够判定DE∥BC的条件是( )
A. ∠DCE+∠DEC= B. ∠EDC=∠DCB
C. ∠BGF=∠DCB D. CD⊥AB,GF⊥AB
5.如图5所示AE∥BD,下列说法不正确的是( )
A.∠1=∠2 B.∠A=∠CBD C.∠BDE+∠DEA=180° D.∠3=∠4
图5 图6 图7
6.如图6所示,能说明AB∥DE的有( )
①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
7.如图7所示,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
8.如图1所示,若∠BEF+______=180°,则AB∥CD.
9.(2008,齐齐哈尔市)如图2所示,请你写一个适当的条件_______, 使AD∥BC.
图2 图3
10.如图3所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
11.如图③, 已知CDE是直线,∠1=,∠A=。
求证:AB∥CD。
证明:∵CDE是一条直线( )
∴∠1+∠2=(平角定义)
∵∠1=( ),∴∠2=( )
又∵∠A=( ),∴∠2=∠A( )
∴AB∥CD( )
12.下列括号内填写的理由是否正确,若有错加以改正
(1)如图④ ∵∠1=,∠2=(已知)∴∠1=∠2(同位角相等)
∴∥(同位角相等,两直线平行)
(2)如图⑤ ∵∥,∥(已知)
∴∥(等量代换)
(3)如图⑥ ∵∠A=,∠ACE=(已知)
∴∠A=∠ACE(内错角相等)
∴BA∥CE(两直线平行)
13.如图⑦ 已知∠2=3∠1,且∠3+∠1=,试说明:AB∥CD
14.已知如图⑧ MP、NP分别平分∠BMF、∠END,且∠1与∠2互余,
求证:AB∥CD
2.3 平行线的性质
一、学习目标
1、经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
2、经历探索平行线特征的过程,掌握平行线的特征,并能解决一些问题。
二、学习重点
平行线的特征的探索
三、学习难点
运用平行线的特征进行有条理的分析、表达
四、学习过程
第一课时
(一)预习准备
(1)预习书50-51页
(2)看书上50页图2-18,并回答四个问题
(二)学习过程
1订正预习作业
2得出平行线的性质
(1)
(2)
(3)
3完成书上50页的做一做
4完成书上51页的随堂练习和习题2.5
第二课时
(一)预习准备
(1)预习书52-54页
(2)回顾:平行线有哪些判定方法和性质?
(3)预习作业
1、如图,已知BE是AB的延长线,并且AD∥BC,AB∥DC,若,则 度, 度。
2、如图,当 ∥ 时,;
当 ∥ 时,;
(二)学习过程
1书上52页例1,例2,例3
2完成书上53页想一想
3完成书上的随堂练习
4完成书上54页的习题2.6
例 如图,已知AD∥BE,AC∥DE,,可推出(1);(2)AB∥CD。填出推理理由。
证明:(1)∵AD∥BE( )
∴( )
又∵AC∥ ( )
∴( )
∴( )
(2)∵AD∥ ( )
∴( )
又∵( )
∴( )
∴AB∥CD( )
变式训练:如图,下列推理所注理由正确的是( )
A、∵DE∥BC ∴(同位角相等,两直线平行)
B、∵ ∴DE∥BC(内错角相等,两直线平行)
C、∵DE∥BC ∴(两直线平行,内错角相等)
D、∵ ∴DE∥BC(两直线平行,同位角相等)
例,如图,已知AB∥CD,求的度数。
变式训练:如图,,已知AB∥CD,试说明
拓展:1、如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,的平分线与的平分线相交于点P,则,试说明理由。
如图,已知EF∥AB,CD⊥AB,,试说明
DG∥BC。
回顾小结:
1、说说平行线的三个性质是什么?
2、平行线的性质与平行线的判定的区别:
判定:角的关系 平行关系
性质:平行关系 角的关系
3、证平行,用判定;知平行,用性质。
2.4用尺规作角
一、学习目标:1、会用尺规作一个角等于已知角。
二、学习重点:1、作一个角等于已知角。
2、作角的和、差、倍数等。
三、学习难点:作角的和、差、倍。
四、学习方法:猜想、实践法
五、学习设计
(一)预习准备
问题的提出:
如右图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB。
(1)请过点C画出与AB平行的另一条边。
(2)如果你只有一个圆规和一把没有刻度的直尺,
你能解决这个问题吗?
(二 )、新课:
内容一:(请按作图步骤和要求操作,别忘了留下作图痕迹)
用尺规作一个角等于已知角.
已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法 图
(1)作射线OˊAˊ
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′A′于点C′;
(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D′;
(5)过点D′作射线 O′B′。则∠A′O′B′就是所求作的角。
(二) 用尺规作一个角等于已知角的倍数:
(3) 已知:∠1
求作: ∠MON,使∠MON=2∠1
∠COD,使∠COD=3∠1
(三) 用尺规作一个角等于已知角的和:
(4) 已知:∠1、∠2、∠3
求作: ∠POQ,使∠POQ=∠1+∠2+∠3
(四) 用尺规作一个角等于已知角的差:
已知:∠、∠、∠
求作:∠AOB,使∠AOB=∠-∠
∠POQ,使∠POQ=∠-∠-∠
求作一个角,使它等于2∠-∠
(六) 综合练习:
1、 下列说法正确的是( )
A、在直线l上取线段AB=a B、作
C、延长射线OA D、反向延长射线OB
2、已知:线段AB、 ∠、∠,求作:分别过点A、点B作∠CAB=∠ 、∠CBA=∠
如图,点P为∠ABC的边AB上的一点,过点P作直线EF//BC
4、已知:直线l和l外一点P,
求作:一条直线,使它经过点P,并与已知直线l平行
已知:△ABC
求作:直线MN,使MN经过点A,且MN//BC
如图,以点B为顶点,射线BA为一边,在∠ABC外再作一个角,使其等于∠ABC
七、 小结:今天我们学习了用尺规作一个角等于已知角,它是一个基本的作图方法。
常见作图语言:(1)作∠XXX=∠XXX。
(2)作XX(射线)平分∠XXX。
(3)过点X作XX⊥XX,垂足为点X。
八、作业:习题2.7 1、2题
回顾与思考
一、课前诊测
1、构建知识框架
2、怎样用尺规作一条线段等于已知线段,作一个角等于已知角?
3、完成书P58-59,知识技能部分。
二、典型例题
例1 已知,如图AB∥CD,直线EF分别截AB,CD于M、N,MG、NH分别是的平分线。试说明MG∥NH。
析:此题考察角平分线、平行线的性质和平行的条件等知识。
证明:∵AB∥CD(已知)
∴ = ( )
∵MG平分(已知)
∴ = = ( )
∵NH平分(已知)
∴ = = ( )
∴ = ( )
∴ ∥ ( )
已知,如图
证明:∵AF与DB相交(已知)
∴ = ( )
∵(已知)
∴ = ( )
∴ ∥ ( )
∴ =∠D( )
∵(已知)
∴ = ( )
∴ ∥ ( )
∴ = ( )
已知,如图AB∥EF,,试判断BC和DE的位置关系,并说明理由。
证明:连接BE,交CD于点O
∵AB∥EF(已知)
∴ = ( )
∵(已知)
∴ — = — ( )
∴ = ( )
∴ ∥ ( )
三、巩固练习
1、下列说法错误的是( )
A、是同位角 B、是同位角
C、是同旁内角 D、是内错角
2、已知:如图,AD∥BC,,求证:AB∥DC。
证:∵AD∥BC(已知)
∴ ( )
又∵(已知)
∴( )
∴
∴AB∥DC( )
3、已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,EF⊥AB,垂足为E,且,,求的度数。
解:∵CD⊥AB,EF⊥AB(已知) ∴∠BEF=∠BDC=90°(垂直的定义)
∴ ∥ ( )
∴ = ( )
∵(已知)
∴ = ( )
∴ ∥ ( )
∴ = ( )
∵(已知)
∴ ( )
4、如图,已知。
推理过程:∵( )
(已知)
∴(等量代换)
∴ ∥ ( )
∴∠3+∠6=180°( )
又∵( )
∴( )
∴( )
5、如图,BE∥CD,,试说明
推理过程: ∵BE∥CD( )
∴ ( )
∵(已知)
∴ ( )
∴BC∥ ( )
∴( )
6、如图,BE平分,DE平分,DG平分,且,试说明BE∥DG.
推理过程:∵BE平分,DE平分( )
∴ , ( )
∵(已知)
∴ =180°
∴ ∥ ( )
∴ ( )
∵DG平分(已知)
∴ ( )
∴( )
∴BE∥DG( )
四、课后练习 <优化>P19 教材P59-60 数学理解 问题解决
2
1
1 ∠3与∠4
2
4
4
3
D
2
E
F
A
1
B
C
C
O
A
B
D
2
1
1 ∠3与∠4
2
4
3
4
P
l
两条直线的位置关系
相交线
平行线
概念
两直线平行的条件
平行线的性质
两直线相交
两直线被第三直线所截
对顶角概念,性质:对顶角
余角概念,性质:同角或等角
补角概念,性质:同角或等角
垂线概念,性质:平面内,过一点
;直线外一点与直线上各点连接的所
有线段中, ;点到直线的距离的概念
“三线八角”及识别
1
2
3
1
2
3
过直线外一点
平行于同一直线的两条直线 。
PAGE
2
一、学习目标:
1、知识目标:在具体情景中了解对顶角、补角、余角,知道对顶角相等、同角或等角的余角相等、同角等角的补角相等,并能解决一些实际问题。
2、能力目标:(1)经历观察、操作、推理、交流等过程,发展空间观念、推理能力和有条理地表达的能力。(2)能运用互为余角、互为补角、对顶角等相关的知识解决一些实际问题。
3、情感目标:在活动中培养学生乐于探究、合作的习惯,体验探索成功、感受创新的乐趣,从而培养学习数学的主动性;进一步体会“数学就在我们身边”,增强学生用数学解决实际问题的意识。
二、学习重点:了解补角、余角、对顶角,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等。
三、学习难点:学生探索同角或等角的余角相等、同角或等角的补角相等、对顶角相等的过程以及对其意义的理解,并能解决一些实际问题。初步的“说理”也是难点之一。
四、学习设计:
(一)预习准备:预习书38、39页,回答下列问题:
(1)在 内,两条直线的位置关系有 和 两种。
(2)若两条直线 ,我们称这两条直线为相交线。
(3)在 内,不相交的两条直线叫 。
(4)下列图形中是对顶角的有 个。
(5)预习作业:
①已知∠1=36°,∠2=54°,那么∠1+∠2=_________
②已知∠1=144°,∠2=36°,那么∠1+∠2=_________
(二)学习过程:
1、创设情境,引入课题
完成书P38议一议,填空:
(1)对顶角具有的特点是①
② 。
(2)对顶角的性质是 。
2、展示新知:
完成书P39想一想,填空:
⑴如果两个角的和等于 ,我们就说这两个角互为余角,简称互余;如果两个角的和等于 ,就说这两个角互为补角,简称互补。
⑵符号语言:若∠1+∠2= 90o , 那么∠1与∠2互余。
若∠3+∠4=180o , 那么∠3与∠4互补。
3、注:(1)“互为”这个词语,与“互为相反数”、“互为倒数”等词语中的含义有联系,均表示成对出现;例如∠1和∠2互余,即∠1是∠2的余角,∠2是∠1的余角。
(2)互为余角以及互为补角的角,主要反映了角的数量关系,而不是角的位置关系。
4、应用新知体验成功
⑴若∠1与∠2互余,则∠1+∠2=__________
⑵若∠1= 90o—∠2,则∠1+∠2=__________
(3)填表:
一个角 30° 70° ∠A
这个角的余角
这个角的补角
5、探讨余角与补角的性质
做书P39 做一做
结论:同角或等角的 相等; 的补角相等。
巩固练习:
(1)如图,∠EDC=∠CDF=90°,∠1=∠2.图中哪 些角互为余角 哪些角互为补角 ∠ADC与
∠BDC有什么关系 为什么
∠ADF与∠BDE有什么关系 为什么
(9)已知:如图∠AOB =∠COD=90°,问:图中有几对相等的角,并说明理由
(三)课堂练习:
1.已知∠A=40°,则∠A的余角等于______.
2.已知:如图所示,AB⊥CD,垂足为点O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.互为对顶角
3.如图所示,直线AB,CD相交于点O,∠BOE=90°,若
∠COE=55°,求∠BOD的度数.
4.如图所示,直线AB与CD相交于点O,OE平分∠AOD,
∠AOC=120°。求∠BOD,∠AOE的度数.
(四)拓展训练:
1.(一题多解题)如图所示,三条直线AB,CD,EF相交于点O,
∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数.
2.(科内交叉题)一个角的补角与这个角的余角的和比平角少10°,求这个角.
3.(课外交叉题)如图所示,当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象.若∠1=42°,∠2=28°,则光的传播方向改变了______度.
4.(实际应用题)如图所示是一个经过改造的台球桌面的示意图,图中4个角上的阴影部分分别表示4个入球袋.如果一个球按图中所示的方向被击出(假设用足够的力气击出,使球可以经过多次反射),那么该球最后落入哪个球袋?在图上画出被击的球所走路程.
七、小结:
互余 互补 对顶角
数量关系
对应图形关系
性质
两条直线的位置关系(2)
学习目标:
1.使学生理解垂线的意义和垂线的第一个性质.
2.会用三角板过一点画已知直线的垂线,培养学生掌握画图的基本技能.
3.通过垂线性质的教学,培养学生发现问题的能力.
二、学习重点:垂线的意义、性质和画法
三、学习难点:垂线的画法
四、学习设计:
(一)预习准备:预习书P41,回答下列问题:
(1) 在平面内的两条直线有 和 两种位置关系,而垂直是 位置关系中的一种特殊情况。
(2) ,那么称这两条直线互相垂直,其中一条直线叫做另一条直线的 ,它们的交点叫 .
(3)通常用符号 表示两条直线互相垂直,“⊥”读作“垂直于”,如AB⊥CD于M,含义是直线AB与直线CD垂直,垂足是M。
(4)如图,若AB⊥CD于O,则∠AOC= °;
若∠BOC=90°,则 。
(二)学习过程:
(1)自主探究:垂线的画法,完成书P41的做一做。
巩固练习:如图,在方格纸上,分别过A画AD的垂线、过B画EF的垂线、过C画GF的垂线.
(2)自主探究:垂线的性质,完成书P41、42想一想。
结论:平面内,过一点 与已知直线垂直。
直线外一点与直线上各点连接的所有线段中, 。
叫点到直线的距离。
巩固练习:如图,通过画图并量得点A到直线的距离等
于 厘米.(精确到0.1厘米)
(三)课堂练习:
1、判断题:
(1)在平面内,过直线外一点有且只有一条直线与已知直线垂直 ( )
(2)过直线上一点不存在直线与已知直线垂直. ( )
(3)过直线外一点A作的垂线,垂线的长度叫做点A到直线的距离.( )
(4)一条线段有无数条垂线. ( )
(5)如图,线段AB与线段CD
不可能互相垂直,因为它们不可能相交.( )
(6)互相垂直的两条直线形成的四个角都等于90 . ( )
2、下列说法错误的个数是( )
一条直线的垂线只有一条;②一条直线的垂线有无数条;
③过一点画一条直线的垂线只能画一条
A、0 B、1 C、2 D、3
3、如果两条直线相交成( ),那么这两条直线互相垂直
A、锐角 B、直角 C、钝角 D、任意一个角
4、过一条线段外一点画这条线段的垂线,垂足在( )
A、这条线段上 B、这条线段的端点上
C、这条线段的延长线上 D、以上都有可能
5、在一个平面内过直线上一点A画的平行线,能画出 条;过直线上一点A画的垂线,能画出 条.
6、在下列各图中,用三角板分别过点C画线段AB的垂线.
(1) (2) (3) (4)
7、将一张长方形纸对折,使OA与OB重合,这时∠AOC是什么角?为什么?
(四)拓展训练:
1、按照题目的要求,分别画出图形,并回答有关问题.
画长3cm的线段AB,取AB的中点O,过O作线段AB的垂线,在上任取一点P,连接PA,PB,量一量线段PA,PB的长度,你发现什么结论?
画一个∠ABC,作出∠ABC的角平分线BD,在BD上任取一点P(除B点外),过P分别作PM⊥BA,PN⊥BC,垂足分别是M,N,量一量线段PM,PN的长度,你发现什么结论?
2、按题目要求画图,并回答相关问题.
画两条直线m,n,使m∥n,在直线m上任取两点A,B,分别过A,B作直线n的垂线,垂足分别为C,D,量一量线段AC,BD的长,你发现了什么结论?
如图,点P是∠AOB内一点,过点P作PM⊥OA,
垂足为M,作PN⊥OB,垂足为N,量一量∠MPN
和∠O,你发现了什么结论?
2.2 探索直线平行的条件(1)
一、学习目标:
1、经历观察、操作、想象、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达的能力。
2、会认由三线八角所成的同位角。
3、掌握平行线公理及平行线的传递性。
4、掌握直线平行的条件并能解决一些问题
二、学习重点:会认各种图形下的同位角,并掌握直线平行的条件是“同位角相等,两直线平行”
三、学习难点:判断两直线平行的说理过程
四、学习设计:
(一)课前准备
(1)预习书44-48页
(2) 思考①什么叫同位角、内错角、同旁内角?②同位角、内错角、同旁内角有什么特征?
(3)预习作业
如图所示,①是 角;它们是由直线 和直线 ,被直线 所截得的;②是 角;它们是由直线 和直线 ,被直线 所截得的;③是 角;它们是由直线 和直线 ,被直线 所截得的。
(二)学习过程
1、两直线被第三直线所截,可形成的角有 , , 。
例1如图是同位角关系的两角是 ,是互补关系的两角是 ,是对顶角的是 。
2、平行判定1:两条直线被第三条直线所截,如果同位角 ,那么这两直线 。
简称: (公理)
如图,可表述为:
∵ ( )
∴ ( )
如图
(1)
(垂直的定义)
∴ ∥ (同位角相等,两直线平行)
(2)用一句精炼的话总结(1)所包含的规律
变式训练:如图所示
1、(已知)
∴ ∥ ( )
2、(已知)
∴ ∥ ( )
例3、如图,已知,直线BC与DF平行吗?为什么?
变式训练:如图,已知,试问a与b平行吗?说说你的理由。
过已知直线a外一点p画a的平行线b
P .
a
平行线公理:过直线外一点有 条直线与这条直线平行。
平行线的传递性:
几何语言:
拓展:
如图,已知,问再添加什么条件可使AB∥CD?试说明理由。
2.2 探索直线平行的条件(2)
一、学习目标:
1、经历观察、操作、想象、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
2、经历探索直线平行的条件的过程,掌握直线平行的条件,并能解决一些问题。
3、会用三角尺过已知直线外一点画这条直线的平行线。
二、学习重点:弄清内错角和同旁内角的意义,会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。
三、学习难点:
会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。
四、学习设计
(一)预习准备
(1)预习书47-48页
(2)回顾:①什么是同位角?什么是内错角?什么是同旁内角?
同位角、内错角、同旁内角的特征(简称“三线八角”)如下表:
基本图形 角的名称 位置特征 图形结构特征
②同位角相等,两直线平行。
(3)预习作业:
如图所示:
(1)如果,那么 ∥
理由是
(2)如果,那么 ∥
理由是
(3)如果,那么 ∥
理由是
(4)如果,那么 ∥
理由是
(二)新课学行判定2:两条直线被第三条直线所截,如果内错角 ,那么这两直线 。
简称:
如图,可表述为:
∵ ( )
∴ ( )
平行判定3:两条直线被第三条直线所截,如果同旁内角 ,那么这两直线 。
简称:
如图,可表述为:
∵ ( )
∴ ( )
例1、如右图,∵∠1=∠2
∴ ∥ ,
∵∠2=
∴ ∥ ,(同位角相等,两直线平行)
∵∠3+∠4=180°
∴ ∥ ,
∴AC∥FG,
变式训练:如图所示,AB⊥BC于点B,BC⊥CD于点C,∠1=∠2,那么EB∥CF吗?为什么?
例2、如图,已知,那么AB∥CD成立吗?请说明理由。
变式训练:如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?
解:为∠1+∠2=180°( )
所以AB∥_______( )
又因为∠1=∠3( )
所以∠2+∠________=180°( )
所以EF∥GH( )
拓展:1、如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
解:AB∥CD 理由如下:
∵BE是∠ABD的平分线,DE是∠BDC的平分线( )
∴∠1= ,∠2= ( )
∵∠1+∠2=90 ( )
∴∠ABD+∠CDB= = =180 。
∴CD∥AB( )
2.如图所示,根据下列条件可推得哪两条直线平行,并说明理由。
(1)∠ABD=∠CDB;(2)∠CBA+∠BAD=180 ;
(3)∠CAD=∠ACB。
当堂测评:
1.下列结论中,不正确的是( )
A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
B.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
C.两条直线被第三条直线所截,那么这两条直线平行。
D.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
2.两条直线被第三条直线所截,下列条件不能判定这两条直线平行的是( )
A.同位角相等 B.内错角相等 C.同旁内角互补 D.同旁内角相等
3.如图① 不能判定∥的一组条件是( )
A.∠1=∠2 B.∠1=∠5 C.∠3=∠4 D.∠2=∠6
4.如图② 能够判定DE∥BC的条件是( )
A. ∠DCE+∠DEC= B. ∠EDC=∠DCB
C. ∠BGF=∠DCB D. CD⊥AB,GF⊥AB
5.如图5所示AE∥BD,下列说法不正确的是( )
A.∠1=∠2 B.∠A=∠CBD C.∠BDE+∠DEA=180° D.∠3=∠4
图5 图6 图7
6.如图6所示,能说明AB∥DE的有( )
①∠1=∠D; ②∠CFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
7.如图7所示,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
8.如图1所示,若∠BEF+______=180°,则AB∥CD.
9.(2008,齐齐哈尔市)如图2所示,请你写一个适当的条件_______, 使AD∥BC.
图2 图3
10.如图3所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
11.如图③, 已知CDE是直线,∠1=,∠A=。
求证:AB∥CD。
证明:∵CDE是一条直线( )
∴∠1+∠2=(平角定义)
∵∠1=( ),∴∠2=( )
又∵∠A=( ),∴∠2=∠A( )
∴AB∥CD( )
12.下列括号内填写的理由是否正确,若有错加以改正
(1)如图④ ∵∠1=,∠2=(已知)∴∠1=∠2(同位角相等)
∴∥(同位角相等,两直线平行)
(2)如图⑤ ∵∥,∥(已知)
∴∥(等量代换)
(3)如图⑥ ∵∠A=,∠ACE=(已知)
∴∠A=∠ACE(内错角相等)
∴BA∥CE(两直线平行)
13.如图⑦ 已知∠2=3∠1,且∠3+∠1=,试说明:AB∥CD
14.已知如图⑧ MP、NP分别平分∠BMF、∠END,且∠1与∠2互余,
求证:AB∥CD
2.3 平行线的性质
一、学习目标
1、经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
2、经历探索平行线特征的过程,掌握平行线的特征,并能解决一些问题。
二、学习重点
平行线的特征的探索
三、学习难点
运用平行线的特征进行有条理的分析、表达
四、学习过程
第一课时
(一)预习准备
(1)预习书50-51页
(2)看书上50页图2-18,并回答四个问题
(二)学习过程
1订正预习作业
2得出平行线的性质
(1)
(2)
(3)
3完成书上50页的做一做
4完成书上51页的随堂练习和习题2.5
第二课时
(一)预习准备
(1)预习书52-54页
(2)回顾:平行线有哪些判定方法和性质?
(3)预习作业
1、如图,已知BE是AB的延长线,并且AD∥BC,AB∥DC,若,则 度, 度。
2、如图,当 ∥ 时,;
当 ∥ 时,;
(二)学习过程
1书上52页例1,例2,例3
2完成书上53页想一想
3完成书上的随堂练习
4完成书上54页的习题2.6
例 如图,已知AD∥BE,AC∥DE,,可推出(1);(2)AB∥CD。填出推理理由。
证明:(1)∵AD∥BE( )
∴( )
又∵AC∥ ( )
∴( )
∴( )
(2)∵AD∥ ( )
∴( )
又∵( )
∴( )
∴AB∥CD( )
变式训练:如图,下列推理所注理由正确的是( )
A、∵DE∥BC ∴(同位角相等,两直线平行)
B、∵ ∴DE∥BC(内错角相等,两直线平行)
C、∵DE∥BC ∴(两直线平行,内错角相等)
D、∵ ∴DE∥BC(两直线平行,同位角相等)
例,如图,已知AB∥CD,求的度数。
变式训练:如图,,已知AB∥CD,试说明
拓展:1、如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,的平分线与的平分线相交于点P,则,试说明理由。
如图,已知EF∥AB,CD⊥AB,,试说明
DG∥BC。
回顾小结:
1、说说平行线的三个性质是什么?
2、平行线的性质与平行线的判定的区别:
判定:角的关系 平行关系
性质:平行关系 角的关系
3、证平行,用判定;知平行,用性质。
2.4用尺规作角
一、学习目标:1、会用尺规作一个角等于已知角。
二、学习重点:1、作一个角等于已知角。
2、作角的和、差、倍数等。
三、学习难点:作角的和、差、倍。
四、学习方法:猜想、实践法
五、学习设计
(一)预习准备
问题的提出:
如右图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB。
(1)请过点C画出与AB平行的另一条边。
(2)如果你只有一个圆规和一把没有刻度的直尺,
你能解决这个问题吗?
(二 )、新课:
内容一:(请按作图步骤和要求操作,别忘了留下作图痕迹)
用尺规作一个角等于已知角.
已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法 图
(1)作射线OˊAˊ
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′A′于点C′;
(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D′;
(5)过点D′作射线 O′B′。则∠A′O′B′就是所求作的角。
(二) 用尺规作一个角等于已知角的倍数:
(3) 已知:∠1
求作: ∠MON,使∠MON=2∠1
∠COD,使∠COD=3∠1
(三) 用尺规作一个角等于已知角的和:
(4) 已知:∠1、∠2、∠3
求作: ∠POQ,使∠POQ=∠1+∠2+∠3
(四) 用尺规作一个角等于已知角的差:
已知:∠、∠、∠
求作:∠AOB,使∠AOB=∠-∠
∠POQ,使∠POQ=∠-∠-∠
求作一个角,使它等于2∠-∠
(六) 综合练习:
1、 下列说法正确的是( )
A、在直线l上取线段AB=a B、作
C、延长射线OA D、反向延长射线OB
2、已知:线段AB、 ∠、∠,求作:分别过点A、点B作∠CAB=∠ 、∠CBA=∠
如图,点P为∠ABC的边AB上的一点,过点P作直线EF//BC
4、已知:直线l和l外一点P,
求作:一条直线,使它经过点P,并与已知直线l平行
已知:△ABC
求作:直线MN,使MN经过点A,且MN//BC
如图,以点B为顶点,射线BA为一边,在∠ABC外再作一个角,使其等于∠ABC
七、 小结:今天我们学习了用尺规作一个角等于已知角,它是一个基本的作图方法。
常见作图语言:(1)作∠XXX=∠XXX。
(2)作XX(射线)平分∠XXX。
(3)过点X作XX⊥XX,垂足为点X。
八、作业:习题2.7 1、2题
回顾与思考
一、课前诊测
1、构建知识框架
2、怎样用尺规作一条线段等于已知线段,作一个角等于已知角?
3、完成书P58-59,知识技能部分。
二、典型例题
例1 已知,如图AB∥CD,直线EF分别截AB,CD于M、N,MG、NH分别是的平分线。试说明MG∥NH。
析:此题考察角平分线、平行线的性质和平行的条件等知识。
证明:∵AB∥CD(已知)
∴ = ( )
∵MG平分(已知)
∴ = = ( )
∵NH平分(已知)
∴ = = ( )
∴ = ( )
∴ ∥ ( )
已知,如图
证明:∵AF与DB相交(已知)
∴ = ( )
∵(已知)
∴ = ( )
∴ ∥ ( )
∴ =∠D( )
∵(已知)
∴ = ( )
∴ ∥ ( )
∴ = ( )
已知,如图AB∥EF,,试判断BC和DE的位置关系,并说明理由。
证明:连接BE,交CD于点O
∵AB∥EF(已知)
∴ = ( )
∵(已知)
∴ — = — ( )
∴ = ( )
∴ ∥ ( )
三、巩固练习
1、下列说法错误的是( )
A、是同位角 B、是同位角
C、是同旁内角 D、是内错角
2、已知:如图,AD∥BC,,求证:AB∥DC。
证:∵AD∥BC(已知)
∴ ( )
又∵(已知)
∴( )
∴
∴AB∥DC( )
3、已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,EF⊥AB,垂足为E,且,,求的度数。
解:∵CD⊥AB,EF⊥AB(已知) ∴∠BEF=∠BDC=90°(垂直的定义)
∴ ∥ ( )
∴ = ( )
∵(已知)
∴ = ( )
∴ ∥ ( )
∴ = ( )
∵(已知)
∴ ( )
4、如图,已知。
推理过程:∵( )
(已知)
∴(等量代换)
∴ ∥ ( )
∴∠3+∠6=180°( )
又∵( )
∴( )
∴( )
5、如图,BE∥CD,,试说明
推理过程: ∵BE∥CD( )
∴ ( )
∵(已知)
∴ ( )
∴BC∥ ( )
∴( )
6、如图,BE平分,DE平分,DG平分,且,试说明BE∥DG.
推理过程:∵BE平分,DE平分( )
∴ , ( )
∵(已知)
∴ =180°
∴ ∥ ( )
∴ ( )
∵DG平分(已知)
∴ ( )
∴( )
∴BE∥DG( )
四、课后练习 <优化>P19 教材P59-60 数学理解 问题解决
2
1
1 ∠3与∠4
2
4
4
3
D
2
E
F
A
1
B
C
C
O
A
B
D
2
1
1 ∠3与∠4
2
4
3
4
P
l
两条直线的位置关系
相交线
平行线
概念
两直线平行的条件
平行线的性质
两直线相交
两直线被第三直线所截
对顶角概念,性质:对顶角
余角概念,性质:同角或等角
补角概念,性质:同角或等角
垂线概念,性质:平面内,过一点
;直线外一点与直线上各点连接的所
有线段中, ;点到直线的距离的概念
“三线八角”及识别
1
2
3
1
2
3
过直线外一点
平行于同一直线的两条直线 。
PAGE
2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
