冀教版数学七年级下册 第十章 一元一次不等式和一元一次不等式组 复习课件 (共21张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 第十章 一元一次不等式和一元一次不等式组 复习课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 07:06:12 | ||
图片预览





文档简介
(共21张PPT)
第十章 一元一次不等式和一元一次不等式组 复习课件
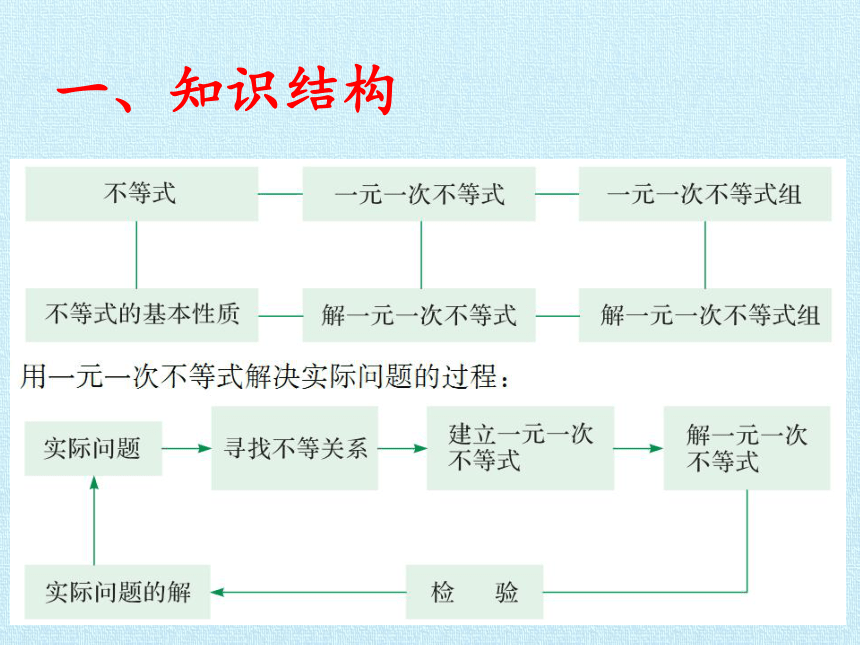
一、知识结构
1.不等式的概念和性质
(1)定义:表示不相等关系的式子叫做不等式。
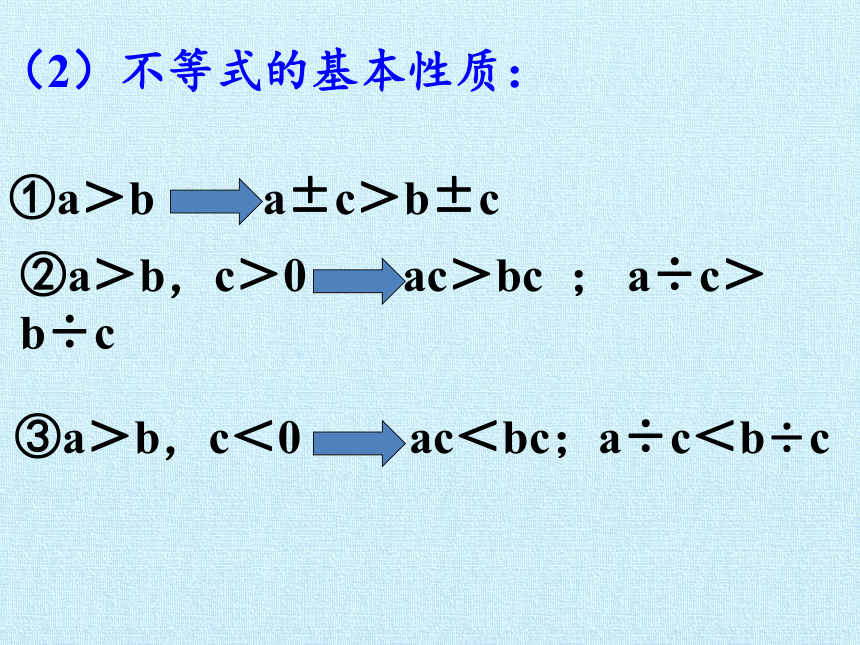
(2)不等式的基本性质:
①a>b a±c>b±c
②a>b,c>0 ac>bc ; a÷c>b÷c
③a>b,c<0 ac<bc;a÷c<b÷c
(3)不等式的解集:
能使不等式成立的未知数的值,
叫做这个不等式的解。
不等式的所有解的集合,叫做
这个不等式的解集。
求不等式的解集的过程,叫做
解不等式。
(4)一元一次不等式和一元一次不等式组
可化为只含有一个未知数,并且未
知数的最高次数是1,系数不等于0的不
等式,叫做一元一次不等式。
最简形式:ax>b或ax<b(a≠0)
标准形式:ax+b>0或ax+b<0(a≠0)
含有相同未知数的几个一元一次不等式组成的不等式组,叫做一元一次不等式组
所有这些一元一次不等式的解集的公共部分,叫做一元一次不等式组的解集。
2.解不等式
(1)解法:类似于解一元一次方程,但注意运用性质3时,不等号方向改变。
(2)一元一次不等式组的解法:
①先求出这个不等式组的各个不等式的解集
②利用数轴确定这个不等式组的解集
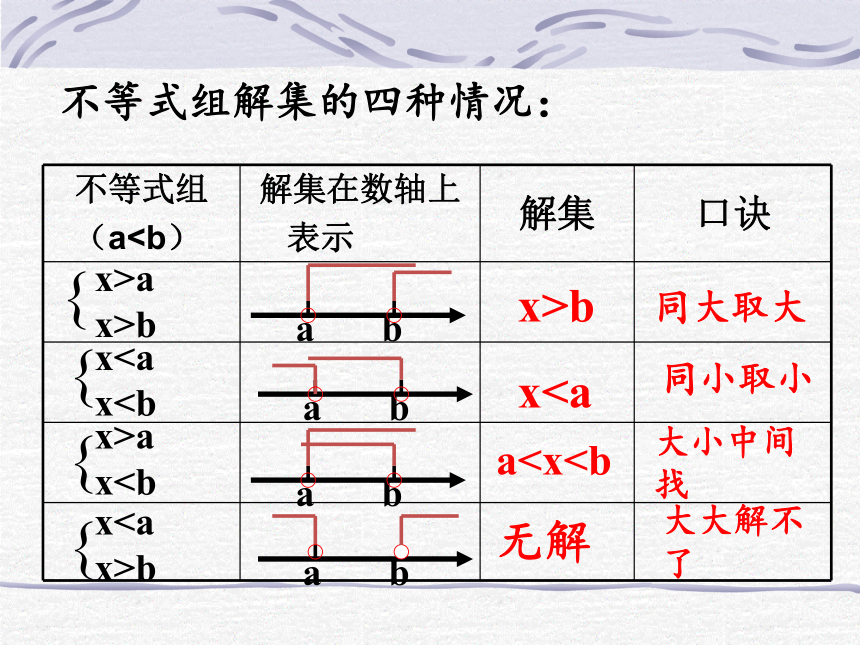
不等式组解集的四种情况:
不等式组 (a{
x>ax>b
{
{
{
xx>axxb
a b
a b
a b
a b
x>b
xa无解
同大取大
同小取小
大小中间找
大大解不了
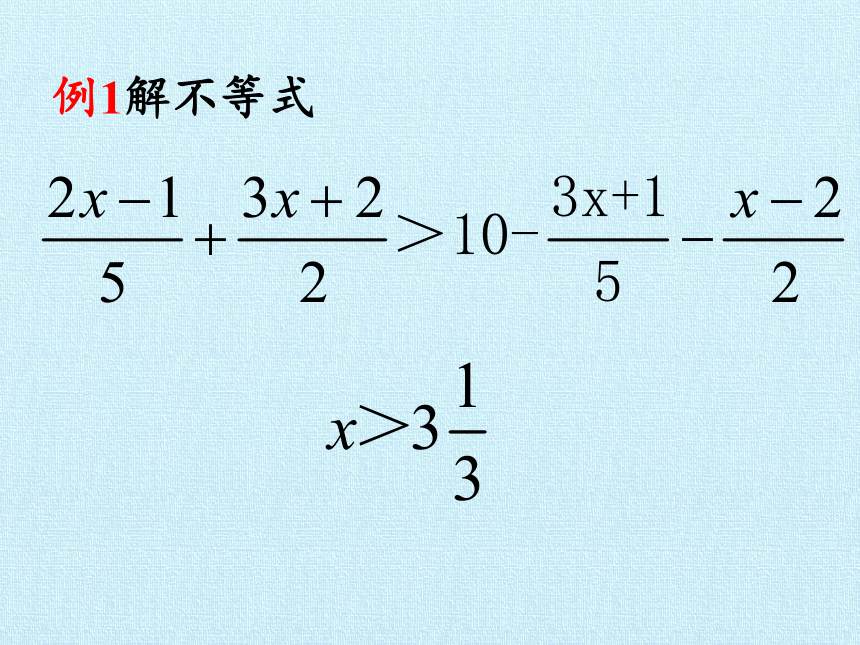
例1解不等式
例2:解不等式组
-3≤x≤1
例3:求不等式
的非负整数解
0,1,2,3
例4:韩日“世界杯”期间,重庆球迷一行56人从旅馆乘出租车到球场为中国队加油,现有A、B两个出租车队,A队比B队少3辆,若全部安排乘A队的车,每辆坐5人,车不够,若每辆坐6人,有的车未坐满;若全部安排乘B队的车,每辆坐4人,车不够,若每辆坐5人,有的车未坐满。求:A、B两队各有几车?
A队10辆车
B队13辆车
达标检测
1.x取什么值时,代数式3x-6的值:
(1)是正数 (2)是负数 (3)是零
解:(1)由题意得:3x-6>0
解得:x>2
∴当x>2时代数式3x-6的值是正数
(2)由题意得:3x-6<0
解得:x<2
∴当x<2时代数式3x-6的值是负数
1.x取什么值时,代数式3x-6的值:
(1)是正数 (2)是负数 (3)是零
解:(3)由题意得:3x-6=0
解得:x=2
∴当x=2时代数式3x-6的值是零。
2.k取什么数值时,代数式
8k2-4(1-3k+2k2)的值不是负数?
解:由题意得:
8k2-4(1-3k+2k2)≥0
解得:k≥
∴当k ≥ 代数式8k2-4(1-3k+2k2)的值不是负数。
3.求不等式10(x+4)+x≤84的非负整数解。
解:解不等式10(x+4)+x≤84得:
x≤4
∴不等式10(x+4)+x≤84的非负整数解是:x=0、1、2、3、4。
4.k为何值时,关于x的不等式
11x-24≤4x-k没有正数解。
解:解关于x的不等式11x-24≤4x-k得:
x≤
又∵x≤0
∴24–k≤0即k≥24
∴当k≥24时,关于x的不等式11x-24≤4x-k没有正数解。
5.关于x的方程x–3(k–2x)=x–1有正数解,求k的取值范围。
解:解关于x的方程x–3(k–2x)=x–1得:
又∵x﹥0
∴3k–1﹥0即 k ﹥
∴ k的取值范围是k ﹥ 。
x =
6.怎样求不等式 的解集?
解:原不等式可化为两个不等式组:
或
即 或
解(1)得 , 解(2)得
∴原不等式的解集是 或 。
谢 谢
第十章 一元一次不等式和一元一次不等式组 复习课件
一、知识结构
1.不等式的概念和性质
(1)定义:表示不相等关系的式子叫做不等式。
(2)不等式的基本性质:
①a>b a±c>b±c
②a>b,c>0 ac>bc ; a÷c>b÷c
③a>b,c<0 ac<bc;a÷c<b÷c
(3)不等式的解集:
能使不等式成立的未知数的值,
叫做这个不等式的解。
不等式的所有解的集合,叫做
这个不等式的解集。
求不等式的解集的过程,叫做
解不等式。
(4)一元一次不等式和一元一次不等式组
可化为只含有一个未知数,并且未
知数的最高次数是1,系数不等于0的不
等式,叫做一元一次不等式。
最简形式:ax>b或ax<b(a≠0)
标准形式:ax+b>0或ax+b<0(a≠0)
含有相同未知数的几个一元一次不等式组成的不等式组,叫做一元一次不等式组
所有这些一元一次不等式的解集的公共部分,叫做一元一次不等式组的解集。
2.解不等式
(1)解法:类似于解一元一次方程,但注意运用性质3时,不等号方向改变。
(2)一元一次不等式组的解法:
①先求出这个不等式组的各个不等式的解集
②利用数轴确定这个不等式组的解集
不等式组解集的四种情况:
不等式组 (a
x>ax>b
{
{
{
x
a b
a b
a b
a b
x>b
x
同大取大
同小取小
大小中间找
大大解不了
例1解不等式
例2:解不等式组
-3≤x≤1
例3:求不等式
的非负整数解
0,1,2,3
例4:韩日“世界杯”期间,重庆球迷一行56人从旅馆乘出租车到球场为中国队加油,现有A、B两个出租车队,A队比B队少3辆,若全部安排乘A队的车,每辆坐5人,车不够,若每辆坐6人,有的车未坐满;若全部安排乘B队的车,每辆坐4人,车不够,若每辆坐5人,有的车未坐满。求:A、B两队各有几车?
A队10辆车
B队13辆车
达标检测
1.x取什么值时,代数式3x-6的值:
(1)是正数 (2)是负数 (3)是零
解:(1)由题意得:3x-6>0
解得:x>2
∴当x>2时代数式3x-6的值是正数
(2)由题意得:3x-6<0
解得:x<2
∴当x<2时代数式3x-6的值是负数
1.x取什么值时,代数式3x-6的值:
(1)是正数 (2)是负数 (3)是零
解:(3)由题意得:3x-6=0
解得:x=2
∴当x=2时代数式3x-6的值是零。
2.k取什么数值时,代数式
8k2-4(1-3k+2k2)的值不是负数?
解:由题意得:
8k2-4(1-3k+2k2)≥0
解得:k≥
∴当k ≥ 代数式8k2-4(1-3k+2k2)的值不是负数。
3.求不等式10(x+4)+x≤84的非负整数解。
解:解不等式10(x+4)+x≤84得:
x≤4
∴不等式10(x+4)+x≤84的非负整数解是:x=0、1、2、3、4。
4.k为何值时,关于x的不等式
11x-24≤4x-k没有正数解。
解:解关于x的不等式11x-24≤4x-k得:
x≤
又∵x≤0
∴24–k≤0即k≥24
∴当k≥24时,关于x的不等式11x-24≤4x-k没有正数解。
5.关于x的方程x–3(k–2x)=x–1有正数解,求k的取值范围。
解:解关于x的方程x–3(k–2x)=x–1得:
又∵x﹥0
∴3k–1﹥0即 k ﹥
∴ k的取值范围是k ﹥ 。
x =
6.怎样求不等式 的解集?
解:原不等式可化为两个不等式组:
或
即 或
解(1)得 , 解(2)得
∴原不等式的解集是 或 。
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
