冀教版数学七年级下册 第八章 读一读 杨辉三角课件(共22张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 第八章 读一读 杨辉三角课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 417.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 12:15:35 | ||
图片预览






文档简介
(共22张PPT)
读一读 杨辉三角
温故知新
多项式乘以多项式:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn.
完全平方公式:
活动一
你能利用多项式乘以多项式法则,求出:
(a+b)1=
(a+b)2=
(a+b)3=
(a+b)4=
(a+b)5=
(a+b)6=
1a+1b
1a2+2ab+1b2
1a3+3a2b+3ab2+1b3
1a4+4a3b+6a2b2+4ab3+1b4
1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
1a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
与二项式展开系数的关系
按某一个字母的次数降序排列
在展开式中,a是按其幂指数由 到 排列的,b是按其幂指数由 到 排列的;首项a的次数与末项b的次数 ,都等于 ;展开式中的项数比二项式乘方的次数 ;展开各项的指数和为
.
高
低
高
低
相同
二项式乘方的次数
多1
二项式乘方的次数
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
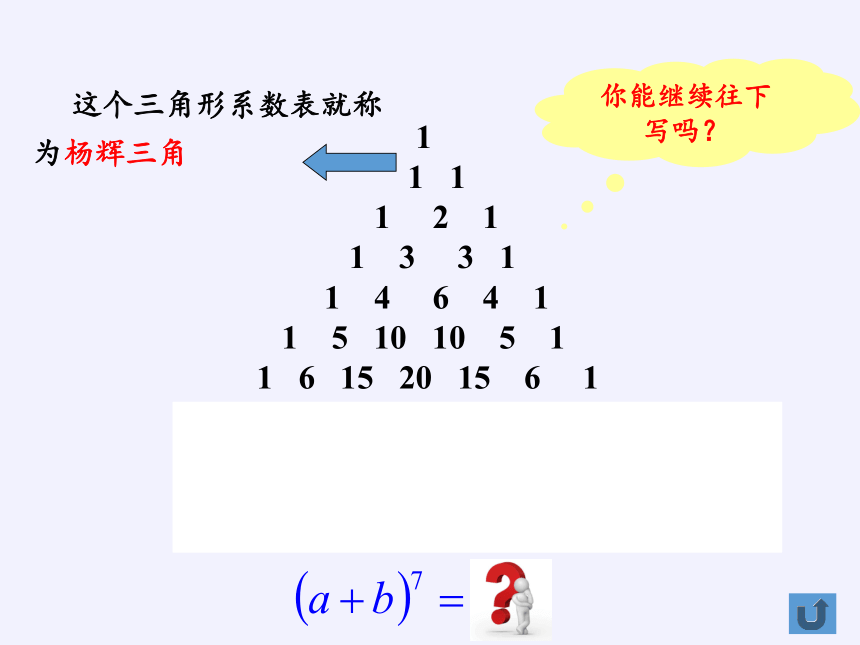
这个三角形系数表就称为杨辉三角
你能继续往下写吗?
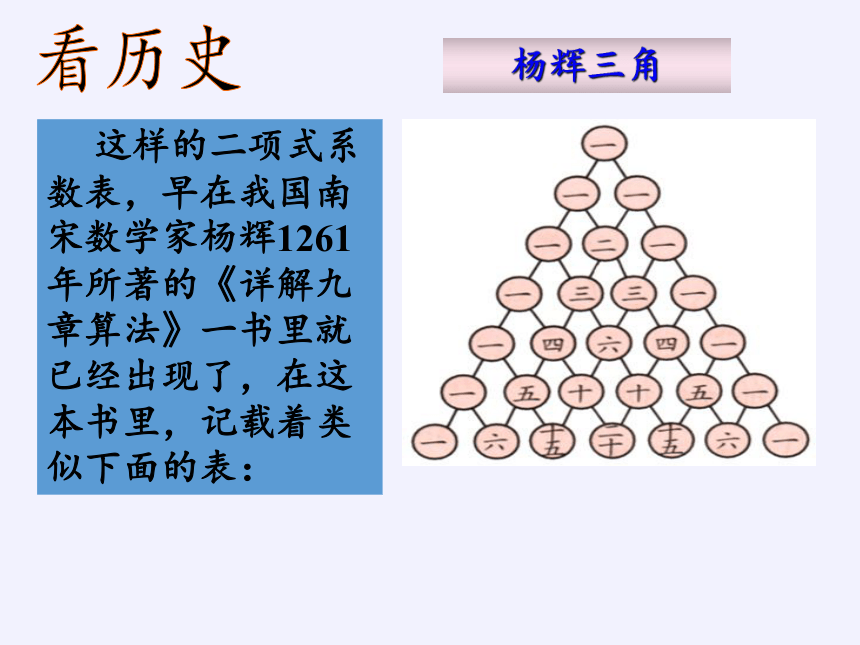
杨辉三角
这样的二项式系数表,早在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书里就已经出现了,在这本书里,记载着类似下面的表:
看历史
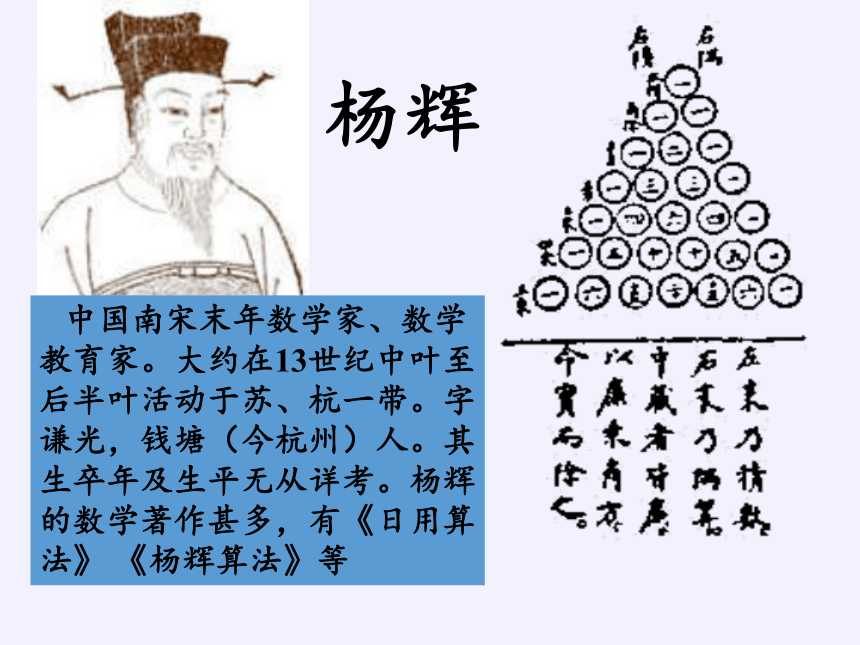
杨辉
中国南宋末年数学家、数学教育家。大约在13世纪中叶至后半叶活动于苏、杭一带。字谦光,钱塘(今杭州)人。其生卒年及生平无从详考。杨辉的数学著作甚多,有《日用算法》 《杨辉算法》等
“杨辉三角”出现在杨辉编著的《详解九章算法》一书中,且我国北宋数学家贾宪(约公元11世纪)已经用过它,这表明我国发现这个表不晚于11世纪.在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角.杨辉三角的发现要比欧洲早500年左右.
在杨辉三角中你发现了哪些规律?
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
活动二
1.三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加
2.杨辉三角具有对称性(对称美),与首末两端“等距离 ”的两个数相等
3.每一行的第二个数就是二项式的次数
4.所有行的第二个数构成等差数列
5.第n行包含n+1个数
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
杨辉三角的基本性质
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
与数字11的幂的关系
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
与数字2的幂的关系
+
+ +
+ + +
杨辉三角第n行中n个数之和等于2的n-1次幂。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
第2k行的数字特征
所有数的和是偶数
弹球游戏,小球向容器内跌落,碰到第一层挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品.
A B C D E F G
在弹球游戏中的应用
AG区奖品最好,BF区奖品次之,CE区奖品第三,D区奖品最差。
“纵横路线图”是数学中的一类有趣的问题.图1是某城市的部分街道图,纵横各有三条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?
A
图1
问:纵横各有几条路呢?
B
杨辉三角的实际应用
我们把图顺时针转45度,使A在正上方,B在正下方,然后在交叉点标上相应的杨辉三角数.B处的杨辉三角数与A到B的走法有什么关系 .
结论:有趣的是,B处所对应的数6,正好是答案( 6).
一般地, 每个交点上的杨辉三角数,就是从A到达该点的方法数.由此看来,杨辉三角与纵横路线图问题有天然的联系
A
B
1
1
1
1
1
2
3
3
6
A
B
D
C
A
B
杨辉三角还有许多奇妙的性质等待着你的发现!
谢 谢
读一读 杨辉三角
温故知新
多项式乘以多项式:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn.
完全平方公式:
活动一
你能利用多项式乘以多项式法则,求出:
(a+b)1=
(a+b)2=
(a+b)3=
(a+b)4=
(a+b)5=
(a+b)6=
1a+1b
1a2+2ab+1b2
1a3+3a2b+3ab2+1b3
1a4+4a3b+6a2b2+4ab3+1b4
1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
1a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
与二项式展开系数的关系
按某一个字母的次数降序排列
在展开式中,a是按其幂指数由 到 排列的,b是按其幂指数由 到 排列的;首项a的次数与末项b的次数 ,都等于 ;展开式中的项数比二项式乘方的次数 ;展开各项的指数和为
.
高
低
高
低
相同
二项式乘方的次数
多1
二项式乘方的次数
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
这个三角形系数表就称为杨辉三角
你能继续往下写吗?
杨辉三角
这样的二项式系数表,早在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书里就已经出现了,在这本书里,记载着类似下面的表:
看历史
杨辉
中国南宋末年数学家、数学教育家。大约在13世纪中叶至后半叶活动于苏、杭一带。字谦光,钱塘(今杭州)人。其生卒年及生平无从详考。杨辉的数学著作甚多,有《日用算法》 《杨辉算法》等
“杨辉三角”出现在杨辉编著的《详解九章算法》一书中,且我国北宋数学家贾宪(约公元11世纪)已经用过它,这表明我国发现这个表不晚于11世纪.在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角.杨辉三角的发现要比欧洲早500年左右.
在杨辉三角中你发现了哪些规律?
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
活动二
1.三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加
2.杨辉三角具有对称性(对称美),与首末两端“等距离 ”的两个数相等
3.每一行的第二个数就是二项式的次数
4.所有行的第二个数构成等差数列
5.第n行包含n+1个数
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
杨辉三角的基本性质
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
与数字11的幂的关系
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
与数字2的幂的关系
+
+ +
+ + +
杨辉三角第n行中n个数之和等于2的n-1次幂。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
第2k行的数字特征
所有数的和是偶数
弹球游戏,小球向容器内跌落,碰到第一层挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品.
A B C D E F G
在弹球游戏中的应用
AG区奖品最好,BF区奖品次之,CE区奖品第三,D区奖品最差。
“纵横路线图”是数学中的一类有趣的问题.图1是某城市的部分街道图,纵横各有三条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?
A
图1
问:纵横各有几条路呢?
B
杨辉三角的实际应用
我们把图顺时针转45度,使A在正上方,B在正下方,然后在交叉点标上相应的杨辉三角数.B处的杨辉三角数与A到B的走法有什么关系 .
结论:有趣的是,B处所对应的数6,正好是答案( 6).
一般地, 每个交点上的杨辉三角数,就是从A到达该点的方法数.由此看来,杨辉三角与纵横路线图问题有天然的联系
A
B
1
1
1
1
1
2
3
3
6
A
B
D
C
A
B
杨辉三角还有许多奇妙的性质等待着你的发现!
谢 谢
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
