沪科版数学八年级下册 18.1勾股定理的-教案
文档属性
| 名称 | 沪科版数学八年级下册 18.1勾股定理的-教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 383.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 09:50:48 | ||
图片预览


文档简介
创新教学
《勾股定理》的教学设计
---------听故事 识定理
学习目标
1、掌握《勾股定理》的内容(重点)
2、通过探索和验证勾股定理的过程,发展对图形性质或数量关系猜想及检验能力。提高学生学习数学的兴趣。 (难点)
3、能应用勾股定理进行简单的计算,感受数形结合之美。
教学过程
一 情境导入-----勾股史话
活动1 听故事
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,你想知道大哲学家发现了什么吗?
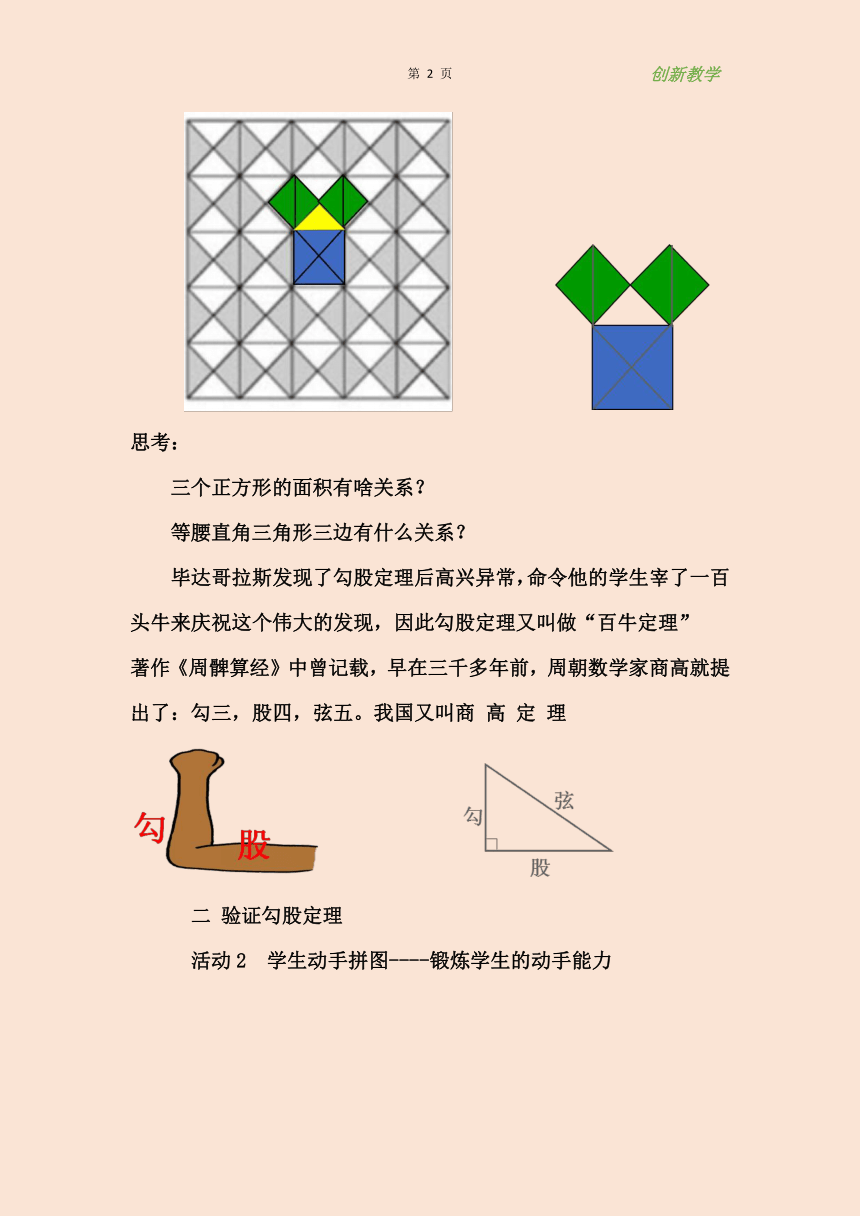
思考:
三个正方形的面积有啥关系?
等腰直角三角形三边有什么关系?
毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”
著作《周髀算经》中曾记载,早在三千多年前,周朝数学家商高就提出了:勾三,股四,弦五。我国又叫商 高 定 理
二 验证勾股定理
活动2 学生动手拼图----锻炼学生的动手能力
用四个直角三角形拼成上右图---赵爽弦图
如下图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你能利用这个图验证勾股定理吗?把你的想法与大家交流一下。
三 勾股定理的证明
1证法一:P53 例题
2证法二:利用赵爽弦图证明
现在我们一起来探索“赵爽弦图”的奥妙吧!
3证法三 美国总统证法
1876年一个周末的傍晚,华盛顿的郊外当时美国共和党议员加菲尔德走着走着,突然发现有两个小孩正在聚精会神地谈论着什么,由于好奇心驱使,加菲尔德循声向两个小孩走去。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”
勾股定理的证明史话:
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
四 美丽的勾股树
五 勾股小常识:
基本勾股数如:大家一定要熟记
3.4.5 5.12.13 7.24.25
2.如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
6、8、10 9、12、15 10、24、26 15、36、39
六 课堂练习:.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
七 课堂小结
学生谈学习本节课的体会
八 课堂作业
1 课本57页,第1、2、3、题
2 查阅有关勾股定理的历史资料
《勾股定理》的教学设计
---------听故事 识定理
学习目标
1、掌握《勾股定理》的内容(重点)
2、通过探索和验证勾股定理的过程,发展对图形性质或数量关系猜想及检验能力。提高学生学习数学的兴趣。 (难点)
3、能应用勾股定理进行简单的计算,感受数形结合之美。
教学过程
一 情境导入-----勾股史话
活动1 听故事
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,你想知道大哲学家发现了什么吗?
思考:
三个正方形的面积有啥关系?
等腰直角三角形三边有什么关系?
毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”
著作《周髀算经》中曾记载,早在三千多年前,周朝数学家商高就提出了:勾三,股四,弦五。我国又叫商 高 定 理
二 验证勾股定理
活动2 学生动手拼图----锻炼学生的动手能力
用四个直角三角形拼成上右图---赵爽弦图
如下图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你能利用这个图验证勾股定理吗?把你的想法与大家交流一下。
三 勾股定理的证明
1证法一:P53 例题
2证法二:利用赵爽弦图证明
现在我们一起来探索“赵爽弦图”的奥妙吧!
3证法三 美国总统证法
1876年一个周末的傍晚,华盛顿的郊外当时美国共和党议员加菲尔德走着走着,突然发现有两个小孩正在聚精会神地谈论着什么,由于好奇心驱使,加菲尔德循声向两个小孩走去。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是加菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”加菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”加菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩说:“先生,你能说出其中的道理吗?”加菲尔德一时语塞,无法解释了,心里很不是滋味。加菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”
勾股定理的证明史话:
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
四 美丽的勾股树
五 勾股小常识:
基本勾股数如:大家一定要熟记
3.4.5 5.12.13 7.24.25
2.如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
6、8、10 9、12、15 10、24、26 15、36、39
六 课堂练习:.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
七 课堂小结
学生谈学习本节课的体会
八 课堂作业
1 课本57页,第1、2、3、题
2 查阅有关勾股定理的历史资料
