山东省淄博市临淄区2012-2013学年九年级下学期期中考试数学试题
文档属性
| 名称 | 山东省淄博市临淄区2012-2013学年九年级下学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 113.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-06 12:23:08 | ||
图片预览




文档简介
2012—2013学年度下学期期中质量检测
初 三 数 学 试 题
本试题共包含三道大题24个小题,满分120分,检测时间120分钟.
一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
1.一组数据4,3,6,9,6,5的中位数和众数分别是
A.5和5.5 B.5.5和6 C.5和6 D.6和6
2. 我市某一周每天的最高气温统计如下:27,28,29,29,30,29,28(单位:℃),则这组数据的极差与众数分别是
A.2,28 B.3,29 C.2,27 D.3,28
3.某中学足球队的18名队员的年龄情况如下表:
年龄(单位:岁) 14 15 16 17 18
人数 3 6 4 4 1
则这些队员年龄的众数和中位数分别是
A.15,15 B.16,15 C.15,16 D.15,15.5
4. 小华所在的八年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是
A.班上比小华高的学生人数不会超过25人;
B.1.65米是该班学生身高的平均水平;
C.这组身高数据的中位数不一定是1.65米;
D.这组身高数据的众数不一定是1.65米.
5.某校开展“节约每一滴水”活动,为了了解开展活动的一个月以来节约用水的情况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水量/m3 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估计这400名同学的家庭一个月节约用水的总量大约是
A. 130m3 B. 135m3 C. 6.5m3 D. 260m3
6.已知一组数据:12,5,9,5,14,下列说法不正确的是
A.平均数是9 B.中位数是9 C.众数是5 D.极差是5
7.已知一组数据10,8,9,,5的众数是8,那么这组数据的方差是
A. 2.8 B. C.2 D.5
8.不能判定一个四边形是平行四边形的条件是
A.两组对边分别平行 B.一组对边平行另一组对边相等
C.一组对边平行且相等 D.两组对边分别相等
9.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连结AB、AD、CD,则四边形ABCD一定是
A.平行四边形 B.矩形 C.菱形 D.梯形
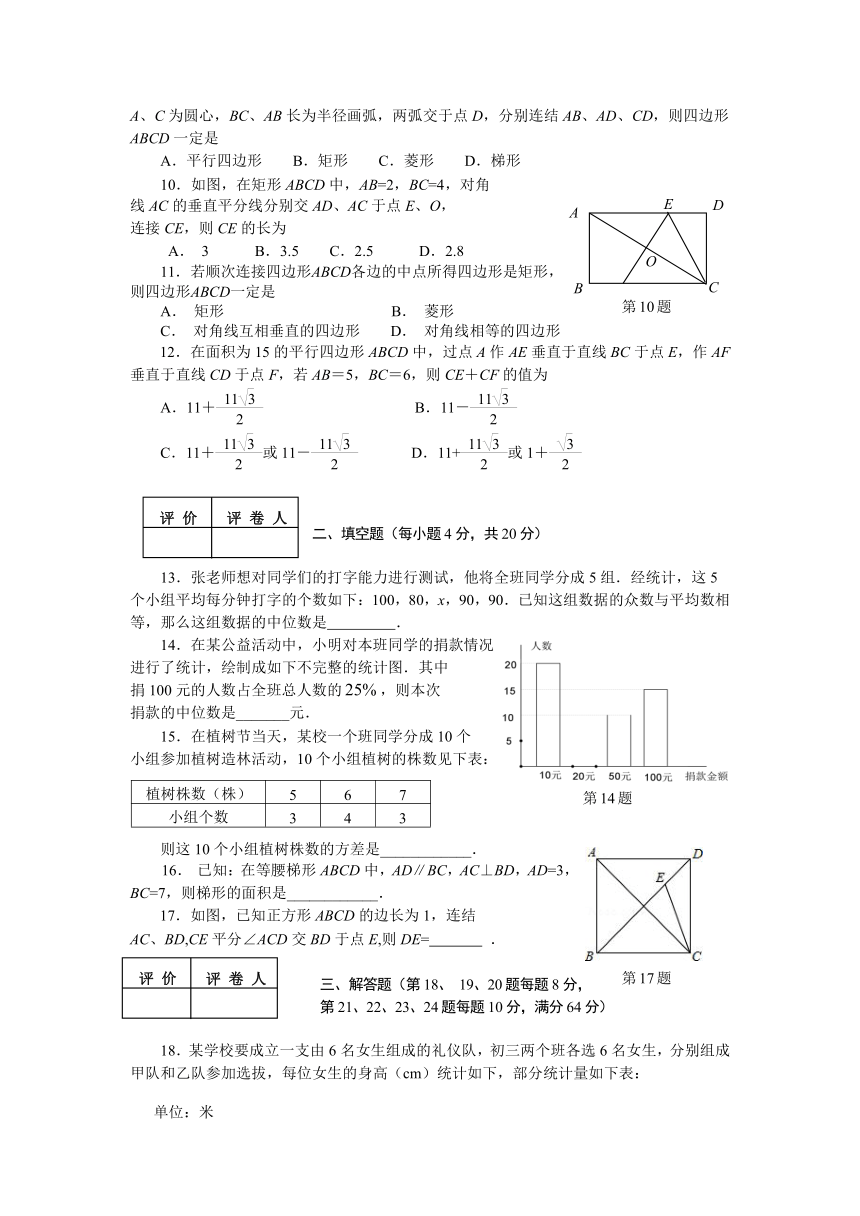
10.如图,在矩形ABCD中,AB=2,BC=4,对角
线AC的垂直平分线分别交AD、AC于点E、O,
连接CE,则CE的长为
A. 3 B.3.5 C.2.5 D.2.8
11.若顺次连接四边形ABCD各边的中点所得四边形是矩形,
则四边形ABCD一定是
A. 矩形 B. 菱形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
12.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为
A.11+ EQ \F( 11 ,2) B.11- EQ \F( 11 ,2)
C.11+ EQ \F( 11 ,2)或11- EQ \F( 11 ,2) D.11+ EQ \F( 11 ,2)或1+ EQ \F( ,2)
二、填空题(每小题4分,共20分)
13.张老师想对同学们的打字能力进行测试,他将全班同学分成5组.经统计,这5个小组平均每分钟打字的个数如下:100,80,x,90,90.已知这组数据的众数与平均数相等,那么这组数据的中位数是 .
14.在某公益活动中,小明对本班同学的捐款情况
进行了统计,绘制成如下不完整的统计图.其中
捐100元的人数占全班总人数的,则本次
捐款的中位数是_______元.
15.在植树节当天,某校一个班同学分成10个
小组参加植树造林活动,10个小组植树的株数见下表:
植树株数(株) 5 6 7
小组个数 3 4 3
则这10个小组植树株数的方差是____________.
16. 已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面积是____________.
17.如图,已知正方形ABCD的边长为1,连结
AC、BD,CE平分∠ACD交BD于点E,则DE= .
三、解答题(第18、 19、20题每题8分,
第21、22、23、24题每题10分,满分64分)
18.某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如下,部分统计量如下表:
平均数 标准差 中位数
甲队 1.72 0.038
乙队 0.025 1.70
(1)求甲队身高的中位数;
(2)如果选拔标准是身高越整齐越好,那么甲乙两个队哪个队被录取?请说明理由.
19.我们约定:如果身高在选定标准的%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,测量出他们的身高(单位:cm),收集并整理如下统计表:
男生序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高(cm) 163 171 173 159 161 174 164 166 169 164
根据以上表格信息解决如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择其中一个统计量作为选定标准,并按此选定标准找出这10名男生具有“普通身高”的男生是哪几位?
(3)若该年级共有280名男生,按(2)中选定标准请你估算出该年级男生中具有“普通身高”的人数约有多少名?
20.如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.
(1)求证:梯形ABCD是等腰梯形;
(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.
21.如图,在菱形ABCD中,AB=2,,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
22.在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH是正方形;
(2)若AD=2,BC=4,求四边形EFGH的面积.
23.如图(1),矩形纸片ABCD,把它沿对角线BD向上折叠.
(1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图痕迹,不写作法.)
(2)折叠后重合部分是什么图形?说明理由.
24.如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.
2012—2013学年度下学期期中质量检测
初三数学试题参考答案
友情提示:
批卷前先做一遍,对学生的方法和结果批前要了解,解题方法只要正确,可参照得分.
一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B D A A D A B A C C D
二、填空题(每小题4分,共20分)
13. 90; 14.20; 15.0.6; 16.25; 17..
三、解答题(第18、 19、20题每题8分,第21、 22、23、24题每题10分,满分64分)18.(1)甲队身高的中位数是=1.73米; …………4分
(2)∵S乙﹤S甲∴乙队身高比较整齐,乙队被录取. …………8分
19.解:(1)平均数为
(cm)…1分
中位数为(cm) …………2分
众数为164(cm) …………3分
(2)选平均数作为标准:
身高满足: …………4分
即时为“普通身高”, …………5分
此时⑦⑧⑨⑩男生的身高具有“普通身高”. …………6分
选中位数作为标准:
身高满足: …………4分
即时为“普通身高”, …………5分
此时①⑦⑧⑩男生的身高具有“普通身高”. …………6分
选众数作为标准:
身高满足: …………4分
即时为“普通身高”, …………5分
此时①⑤⑦⑧⑩男生的身高具有“普通身高”. …………6分
(3)以平均数作为标准,估计全年级男生中具有“普通身高”的人数约为:
(人); …………8分
以中位数作为标准,估计全年级男生中具有“普通身高”的人数约为:
(人). …………8分
以众数作为标准,估计全年级男生中具有“普通身高”的人数约为:
(人). …………8分
20.解:(1)证明:∵AD∥BC,
∴∠DEC=∠EDA,∠BEA=∠EAD. …1分
又∵EA=ED,∴∠EAD=∠EDA.
∴∠DEC=∠AEB. …………2分
又∵EB=EC,∴△DEC≌△AEB. …………3分
∴AB=CD.∴梯形ABCD是等腰梯形. …………4分
(2)当AB⊥AC时,四边形AECD是菱形. …5分
证明:∵AD∥BC,BE=EC=AD,
∴四边形ABED和四边形AECD均为平行四边形.
∴AD=EC ,AE=CD.…………6分
∵AB⊥AC,
∴AE=BE=EC.
∴AE=EC=CD=AD.
∴四边形AECD是菱形.
过A作AG⊥BE于点G,
∵AE=CE=BE=AB=2,
∴△ABE是等边三角形,∠AEB=60°.
∴AG=. …………7分
∴S菱形AECD=2×=.…………8分
21.(1)证明:∵四边形ABCD是菱形,∴ND∥AM
∴∠NDE=∠EAM ,∠END=∠EMA …………2分
又∵点E是AD中点,∴DE=AE …………3分
∴△DEN≌△AEM, …………4分
∴ND=AM …………5分
∴四边形AMDN是平行四边形 …………6分
(2)①1;②2 …………10分
22.(1)∵E、F分别是AB、BC的中点
∴EF是三角形ABC的中位线
∴EF∥AC、EF=AC, ………1分
同理得,HG ∥AC,HG=AC,EH∥BD, EH=BD, FG∥BD, FG=BD, …2分
∵AC=BD∴EH=FG=EF=HG
∴四边形EFGH为菱形 ………3分
∵EF∥AC, EH∥BD, AC⊥BD
∴∠EHG=90° ………4分
∴菱形EFGH为正方形. ………5分
(2)∵在梯形ABCD中,E、G分别是AB、CD的中点.
∴EG为梯形ABCD的中位线
∴EG=(AD+BC)=3 ………8分
正方形EFGH的面积=EG2=4.5 …………10分
23.解:(1)作法参考:
方法1:作∠BDG=∠BDC,在射线DG上截取DE=DC,连接BE;
方法2:作∠DBH=∠DBC,在射线BH上截取BE=BC,连接DE;
方法3:作∠BDG=∠BDC,过B点作BH⊥DG,垂足为E
方法4:作∠DBH=∠DBC,过D点作DG⊥BH,垂足为E;
方法5:分别以D、B为圆心,DC、BC的长为半径画弧,两弧交于点E,连接DE、BE
(注:作法合理均可得分)
∴△DEB为所求作的图形. ………5分
(2)等腰三角形. ………6分
证明:∵△BDE是△BDC沿BD折叠而成,
∴△BDE≌△BDC,
∴∠FDB=∠CDB, ………7分
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABD=∠BDC, ………8分
∴∠FDB=∠BDC, ∴DF=BF,…9分
∴△BDF是等腰三角形. …10分
24.证明:(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°, ……2分
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM=AD,CN=BC,
∴AM=CN, ……3分
在△MAB和△NDC中,
∵AB=CD,∠A=∠C=90°,AM=CN,
∴△MAB≌△NDC; ……5分
(2)四边形MPNQ是菱形, ……6分
理由如下:连接AN,易证:△ABN≌△BAM, ……7分
∴AN=BM,∠ABM=∠CDN,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴,
∴PM=NQ,
∵DM=BN,DQ=BP,∠MDQ=∠NBP,
∴△MQD≌△NPB,
∴MQ=PN.
∴四边形MPNQ是平行四边形, ……8分
∵M是AB中点,Q是DN中点,
∴MQ=AN,
∴MQ=BM,
∴MP=BM,
∴MP=MQ, ……9分
∴四边形MQNP是菱形. ……10分
评 价
评 卷 人
第9题
第10题
A
B
C
D
E
O
评 价
评 卷 人
第14题
第17题
评 价
评 卷 人
单位:米
第18题
第20题
A
C
B
D
E
F
第21题
A
D
C
B
M
N
P
Q
第24题
第20题
A
C
B
D
E
F
G
第22题
第23题
A
D
C
B
M
N
P
Q
第24题
初 三 数 学 试 题
本试题共包含三道大题24个小题,满分120分,检测时间120分钟.
一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
1.一组数据4,3,6,9,6,5的中位数和众数分别是
A.5和5.5 B.5.5和6 C.5和6 D.6和6
2. 我市某一周每天的最高气温统计如下:27,28,29,29,30,29,28(单位:℃),则这组数据的极差与众数分别是
A.2,28 B.3,29 C.2,27 D.3,28
3.某中学足球队的18名队员的年龄情况如下表:
年龄(单位:岁) 14 15 16 17 18
人数 3 6 4 4 1
则这些队员年龄的众数和中位数分别是
A.15,15 B.16,15 C.15,16 D.15,15.5
4. 小华所在的八年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是
A.班上比小华高的学生人数不会超过25人;
B.1.65米是该班学生身高的平均水平;
C.这组身高数据的中位数不一定是1.65米;
D.这组身高数据的众数不一定是1.65米.
5.某校开展“节约每一滴水”活动,为了了解开展活动的一个月以来节约用水的情况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水量/m3 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估计这400名同学的家庭一个月节约用水的总量大约是
A. 130m3 B. 135m3 C. 6.5m3 D. 260m3
6.已知一组数据:12,5,9,5,14,下列说法不正确的是
A.平均数是9 B.中位数是9 C.众数是5 D.极差是5
7.已知一组数据10,8,9,,5的众数是8,那么这组数据的方差是
A. 2.8 B. C.2 D.5
8.不能判定一个四边形是平行四边形的条件是
A.两组对边分别平行 B.一组对边平行另一组对边相等
C.一组对边平行且相等 D.两组对边分别相等
9.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连结AB、AD、CD,则四边形ABCD一定是
A.平行四边形 B.矩形 C.菱形 D.梯形
10.如图,在矩形ABCD中,AB=2,BC=4,对角
线AC的垂直平分线分别交AD、AC于点E、O,
连接CE,则CE的长为
A. 3 B.3.5 C.2.5 D.2.8
11.若顺次连接四边形ABCD各边的中点所得四边形是矩形,
则四边形ABCD一定是
A. 矩形 B. 菱形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
12.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为
A.11+ EQ \F( 11 ,2) B.11- EQ \F( 11 ,2)
C.11+ EQ \F( 11 ,2)或11- EQ \F( 11 ,2) D.11+ EQ \F( 11 ,2)或1+ EQ \F( ,2)
二、填空题(每小题4分,共20分)
13.张老师想对同学们的打字能力进行测试,他将全班同学分成5组.经统计,这5个小组平均每分钟打字的个数如下:100,80,x,90,90.已知这组数据的众数与平均数相等,那么这组数据的中位数是 .
14.在某公益活动中,小明对本班同学的捐款情况
进行了统计,绘制成如下不完整的统计图.其中
捐100元的人数占全班总人数的,则本次
捐款的中位数是_______元.
15.在植树节当天,某校一个班同学分成10个
小组参加植树造林活动,10个小组植树的株数见下表:
植树株数(株) 5 6 7
小组个数 3 4 3
则这10个小组植树株数的方差是____________.
16. 已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面积是____________.
17.如图,已知正方形ABCD的边长为1,连结
AC、BD,CE平分∠ACD交BD于点E,则DE= .
三、解答题(第18、 19、20题每题8分,
第21、22、23、24题每题10分,满分64分)
18.某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如下,部分统计量如下表:
平均数 标准差 中位数
甲队 1.72 0.038
乙队 0.025 1.70
(1)求甲队身高的中位数;
(2)如果选拔标准是身高越整齐越好,那么甲乙两个队哪个队被录取?请说明理由.
19.我们约定:如果身高在选定标准的%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,测量出他们的身高(单位:cm),收集并整理如下统计表:
男生序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高(cm) 163 171 173 159 161 174 164 166 169 164
根据以上表格信息解决如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择其中一个统计量作为选定标准,并按此选定标准找出这10名男生具有“普通身高”的男生是哪几位?
(3)若该年级共有280名男生,按(2)中选定标准请你估算出该年级男生中具有“普通身高”的人数约有多少名?
20.如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.
(1)求证:梯形ABCD是等腰梯形;
(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.
21.如图,在菱形ABCD中,AB=2,,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
22.在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH是正方形;
(2)若AD=2,BC=4,求四边形EFGH的面积.
23.如图(1),矩形纸片ABCD,把它沿对角线BD向上折叠.
(1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图痕迹,不写作法.)
(2)折叠后重合部分是什么图形?说明理由.
24.如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.
2012—2013学年度下学期期中质量检测
初三数学试题参考答案
友情提示:
批卷前先做一遍,对学生的方法和结果批前要了解,解题方法只要正确,可参照得分.
一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B D A A D A B A C C D
二、填空题(每小题4分,共20分)
13. 90; 14.20; 15.0.6; 16.25; 17..
三、解答题(第18、 19、20题每题8分,第21、 22、23、24题每题10分,满分64分)18.(1)甲队身高的中位数是=1.73米; …………4分
(2)∵S乙﹤S甲∴乙队身高比较整齐,乙队被录取. …………8分
19.解:(1)平均数为
(cm)…1分
中位数为(cm) …………2分
众数为164(cm) …………3分
(2)选平均数作为标准:
身高满足: …………4分
即时为“普通身高”, …………5分
此时⑦⑧⑨⑩男生的身高具有“普通身高”. …………6分
选中位数作为标准:
身高满足: …………4分
即时为“普通身高”, …………5分
此时①⑦⑧⑩男生的身高具有“普通身高”. …………6分
选众数作为标准:
身高满足: …………4分
即时为“普通身高”, …………5分
此时①⑤⑦⑧⑩男生的身高具有“普通身高”. …………6分
(3)以平均数作为标准,估计全年级男生中具有“普通身高”的人数约为:
(人); …………8分
以中位数作为标准,估计全年级男生中具有“普通身高”的人数约为:
(人). …………8分
以众数作为标准,估计全年级男生中具有“普通身高”的人数约为:
(人). …………8分
20.解:(1)证明:∵AD∥BC,
∴∠DEC=∠EDA,∠BEA=∠EAD. …1分
又∵EA=ED,∴∠EAD=∠EDA.
∴∠DEC=∠AEB. …………2分
又∵EB=EC,∴△DEC≌△AEB. …………3分
∴AB=CD.∴梯形ABCD是等腰梯形. …………4分
(2)当AB⊥AC时,四边形AECD是菱形. …5分
证明:∵AD∥BC,BE=EC=AD,
∴四边形ABED和四边形AECD均为平行四边形.
∴AD=EC ,AE=CD.…………6分
∵AB⊥AC,
∴AE=BE=EC.
∴AE=EC=CD=AD.
∴四边形AECD是菱形.
过A作AG⊥BE于点G,
∵AE=CE=BE=AB=2,
∴△ABE是等边三角形,∠AEB=60°.
∴AG=. …………7分
∴S菱形AECD=2×=.…………8分
21.(1)证明:∵四边形ABCD是菱形,∴ND∥AM
∴∠NDE=∠EAM ,∠END=∠EMA …………2分
又∵点E是AD中点,∴DE=AE …………3分
∴△DEN≌△AEM, …………4分
∴ND=AM …………5分
∴四边形AMDN是平行四边形 …………6分
(2)①1;②2 …………10分
22.(1)∵E、F分别是AB、BC的中点
∴EF是三角形ABC的中位线
∴EF∥AC、EF=AC, ………1分
同理得,HG ∥AC,HG=AC,EH∥BD, EH=BD, FG∥BD, FG=BD, …2分
∵AC=BD∴EH=FG=EF=HG
∴四边形EFGH为菱形 ………3分
∵EF∥AC, EH∥BD, AC⊥BD
∴∠EHG=90° ………4分
∴菱形EFGH为正方形. ………5分
(2)∵在梯形ABCD中,E、G分别是AB、CD的中点.
∴EG为梯形ABCD的中位线
∴EG=(AD+BC)=3 ………8分
正方形EFGH的面积=EG2=4.5 …………10分
23.解:(1)作法参考:
方法1:作∠BDG=∠BDC,在射线DG上截取DE=DC,连接BE;
方法2:作∠DBH=∠DBC,在射线BH上截取BE=BC,连接DE;
方法3:作∠BDG=∠BDC,过B点作BH⊥DG,垂足为E
方法4:作∠DBH=∠DBC,过D点作DG⊥BH,垂足为E;
方法5:分别以D、B为圆心,DC、BC的长为半径画弧,两弧交于点E,连接DE、BE
(注:作法合理均可得分)
∴△DEB为所求作的图形. ………5分
(2)等腰三角形. ………6分
证明:∵△BDE是△BDC沿BD折叠而成,
∴△BDE≌△BDC,
∴∠FDB=∠CDB, ………7分
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABD=∠BDC, ………8分
∴∠FDB=∠BDC, ∴DF=BF,…9分
∴△BDF是等腰三角形. …10分
24.证明:(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°, ……2分
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM=AD,CN=BC,
∴AM=CN, ……3分
在△MAB和△NDC中,
∵AB=CD,∠A=∠C=90°,AM=CN,
∴△MAB≌△NDC; ……5分
(2)四边形MPNQ是菱形, ……6分
理由如下:连接AN,易证:△ABN≌△BAM, ……7分
∴AN=BM,∠ABM=∠CDN,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴,
∴PM=NQ,
∵DM=BN,DQ=BP,∠MDQ=∠NBP,
∴△MQD≌△NPB,
∴MQ=PN.
∴四边形MPNQ是平行四边形, ……8分
∵M是AB中点,Q是DN中点,
∴MQ=AN,
∴MQ=BM,
∴MP=BM,
∴MP=MQ, ……9分
∴四边形MQNP是菱形. ……10分
评 价
评 卷 人
第9题
第10题
A
B
C
D
E
O
评 价
评 卷 人
第14题
第17题
评 价
评 卷 人
单位:米
第18题
第20题
A
C
B
D
E
F
第21题
A
D
C
B
M
N
P
Q
第24题
第20题
A
C
B
D
E
F
G
第22题
第23题
A
D
C
B
M
N
P
Q
第24题
同课章节目录
