矩形的定义和性质 课件
图片预览



文档简介
课件31张PPT。第十九章 四边形——矩形的定义、性质人教版八年级(下册)19.2 特殊平行四边形§19.2 .1矩形的定义、性质矩形www.21cnjy.com矩形的定义和性质温故而知新平行四边形有哪些性质?对边平行
且相等对角相等
邻角互补对角线互
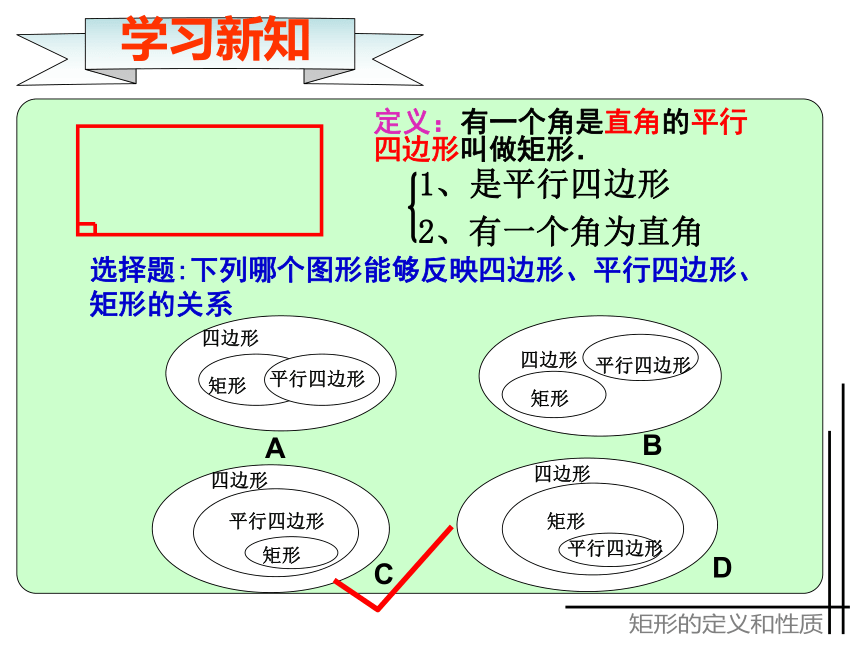
相平分中心对称图形细心观察矩形的定义和性质细心观察平行四边形内角的变化 定义:有一个角是直角的平行四边形叫做矩形.1、是平行四边形2、有一个角为直角选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系矩形的定义和性质学习新知1、平行四边形变成矩形时,图形的内角
有何特征?
2、平行四边形变成矩形时,两条对角线
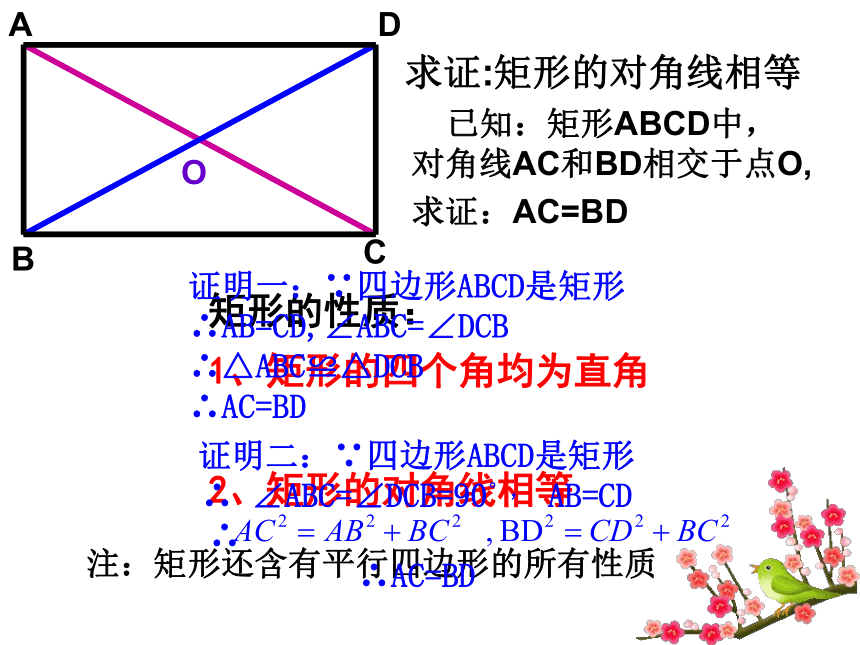
的长度有什么关系?动手试一试矩形的定义和性质在操作过程中,请你思考下列问题:AODCB求证:矩形的对角线相等已知:矩形ABCD中,
对角线AC和BD相交于点O,求证:AC=BD矩形的性质:
1、矩形的四个角均为直角
2、矩形的对角线相等注:矩形还含有平行四边形的所有性质证明二:∵四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°, AB=CD
∴
∴AC=BD证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
∴△ABC≌△DCB
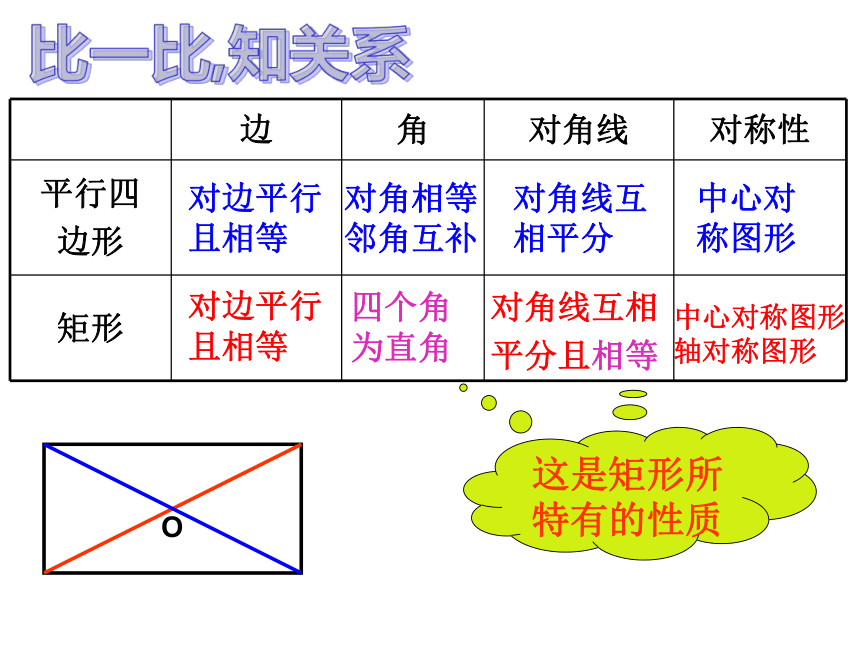
∴AC=BD比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形O学以致用矩形的定义和性质1. 矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分2、 矩形的一组邻边长分别是3cm和4cm,
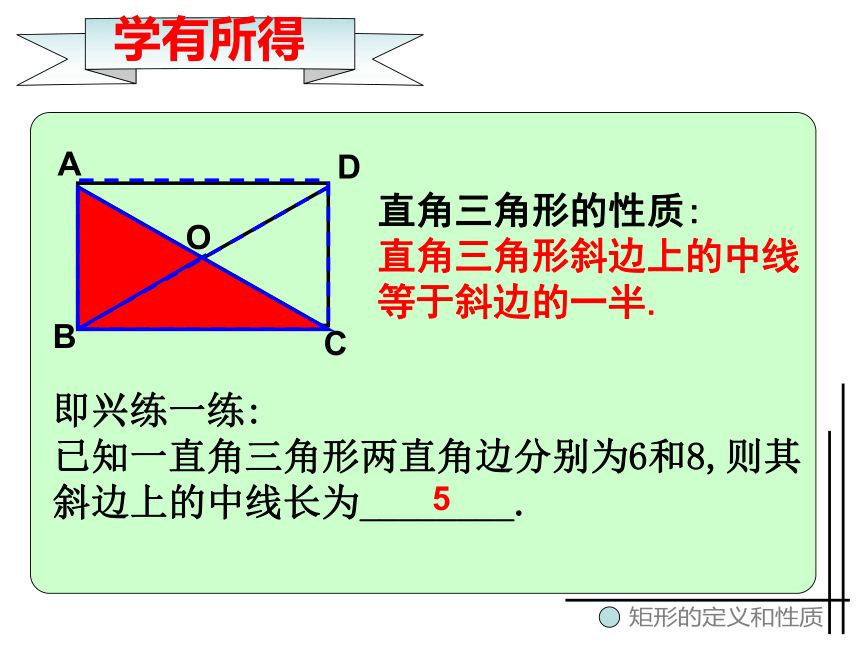
则它的对角线长是 cm. A5AODCB直角三角形的性质:
直角三角形斜边上的中线
等于斜边的一半.即兴练一练:
已知一直角三角形两直角边分别为6和8,则其
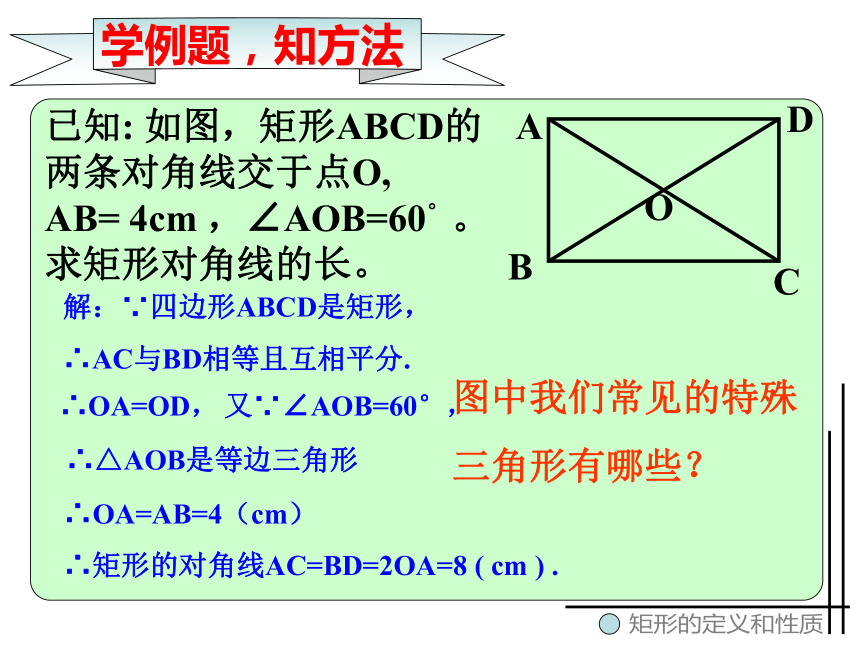
斜边上的中线长为________.5矩形的定义和性质学有所得学例题,知方法矩形的定义和性质图中我们常见的特殊
三角形有哪些?BO解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.∴OA=OD,又∵∠AOB=60°,∴OA=AB=4(cm)
∴矩形的对角线AC=BD=2OA=8 ( cm ) .∴△AOB是等边三角形已知: 如图,矩形ABCD的
两条对角线交于点O,
AB= 4cm ,∠AOB=60°。
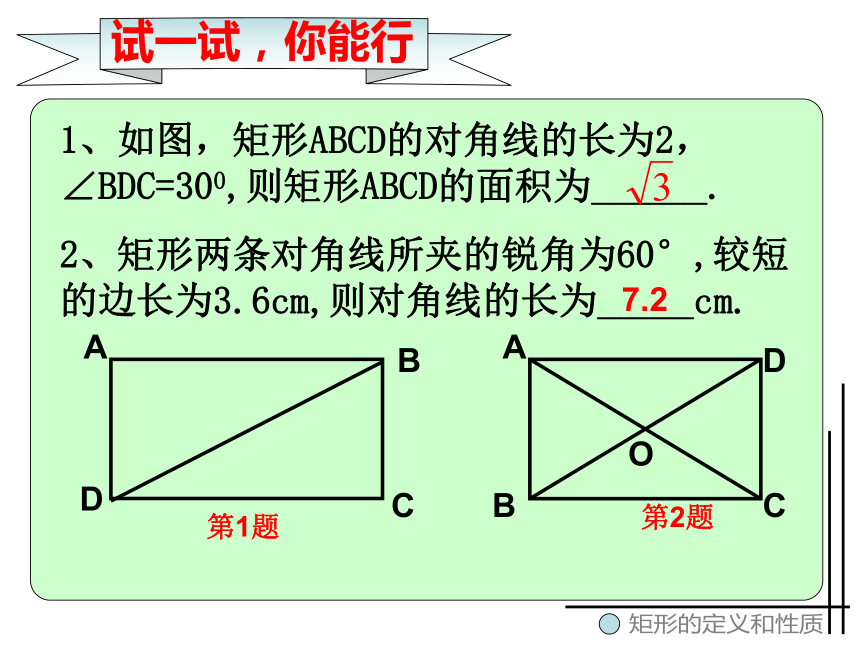
求矩形对角线的长。 DCA矩形的定义和性质1、如图,矩形ABCD的对角线的长为2,∠BDC=300,则矩形ABCD的面积为______.
2、矩形两条对角线所夹的锐角为60°,较短的边长为3.6cm,则对角线的长为_____cm.7.2试一试,你能行试一试,你能行矩形的定义和性质 3、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____ADCBO161、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4∵AE平分∠BAD
∴∠BAE=45°∴AB=BE=4∴BC=7∴矩形ABCD的周长为22cm比一比,看谁做得快!矩形的定义和性质说说:今天的收获……
你还有什么不明白的地方……矩形的定义和性质4、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;1、矩形定义:
有一个角是直角的平行四边形叫矩形矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等歇闲小站 作 业4、9、四边形1、2、33、 学海 无涯1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD试一试已知矩形ABCD,请找出所有的直角三角形和等腰三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC、△ADO、 △DOC、
△COB、 △AOB、600如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分。又 ∠AOB=60°,∴ ΔOAB是等边三角形∴OA=AB=4(cm)∴ AC=BD = 2OA=2×4=8(cm)
∴ OA = OB。变式:若BD=8cm,∠AOD=120°,求边AB的长。
O1200OABCD公平,因为OB=OD = OA=OC生活链接---投圈游戏OABCDOB=OD = OA=OC推论:直角三角形斜边上的中线等于
斜边的一半。
= AC= BD 在 中,∠ABC=900 ,BO是斜边AC上的中线
OB = AC练一练 1. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510 学海 无涯A2.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm2D3.在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.作斜边AB边的中线则 AD=CD= AB∴AC=AD=CD= AB又∵AB=2AC∴⊿ACD是等边三角形∴∠A=60°
∴∠B=30 °练习4.矩形ABCD中,AB=2BC,AE=AB,求∠EBC的度数ABCDE5.设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1________S2.6.已知如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=1200,求∠EAO的度数和∠OEA的度数 。7.已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。2、如图,矩形AEFG和矩形ADCB的大小、形状完全相同,把它们拼成如图所示的L型图案,已知∠FAE=30°,分别求∠1、∠2的度数。 解:依题意可知:
∠FAE=∠DCA=30 °,AF=AC∴∠1=45 °,∴∠2=∠ACF-∠ACD=15 °∴∠DAC=60 °,∴∠FAC=90 °,矩形的定义和性质挑战你的思维 如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢?阅读下面短文矩形的定义和性质
且相等对角相等
邻角互补对角线互
相平分中心对称图形细心观察矩形的定义和性质细心观察平行四边形内角的变化 定义:有一个角是直角的平行四边形叫做矩形.1、是平行四边形2、有一个角为直角选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系矩形的定义和性质学习新知1、平行四边形变成矩形时,图形的内角
有何特征?
2、平行四边形变成矩形时,两条对角线
的长度有什么关系?动手试一试矩形的定义和性质在操作过程中,请你思考下列问题:AODCB求证:矩形的对角线相等已知:矩形ABCD中,
对角线AC和BD相交于点O,求证:AC=BD矩形的性质:
1、矩形的四个角均为直角
2、矩形的对角线相等注:矩形还含有平行四边形的所有性质证明二:∵四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°, AB=CD
∴
∴AC=BD证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
∴△ABC≌△DCB
∴AC=BD比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形O学以致用矩形的定义和性质1. 矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分2、 矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是 cm. A5AODCB直角三角形的性质:
直角三角形斜边上的中线
等于斜边的一半.即兴练一练:
已知一直角三角形两直角边分别为6和8,则其
斜边上的中线长为________.5矩形的定义和性质学有所得学例题,知方法矩形的定义和性质图中我们常见的特殊
三角形有哪些?BO解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.∴OA=OD,又∵∠AOB=60°,∴OA=AB=4(cm)
∴矩形的对角线AC=BD=2OA=8 ( cm ) .∴△AOB是等边三角形已知: 如图,矩形ABCD的
两条对角线交于点O,
AB= 4cm ,∠AOB=60°。
求矩形对角线的长。 DCA矩形的定义和性质1、如图,矩形ABCD的对角线的长为2,∠BDC=300,则矩形ABCD的面积为______.
2、矩形两条对角线所夹的锐角为60°,较短的边长为3.6cm,则对角线的长为_____cm.7.2试一试,你能行试一试,你能行矩形的定义和性质 3、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____ADCBO161、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4∵AE平分∠BAD
∴∠BAE=45°∴AB=BE=4∴BC=7∴矩形ABCD的周长为22cm比一比,看谁做得快!矩形的定义和性质说说:今天的收获……
你还有什么不明白的地方……矩形的定义和性质4、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;1、矩形定义:
有一个角是直角的平行四边形叫矩形矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等歇闲小站 作 业4、9、四边形1、2、33、 学海 无涯1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD试一试已知矩形ABCD,请找出所有的直角三角形和等腰三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC、△ADO、 △DOC、
△COB、 △AOB、600如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分。又 ∠AOB=60°,∴ ΔOAB是等边三角形∴OA=AB=4(cm)∴ AC=BD = 2OA=2×4=8(cm)
∴ OA = OB。变式:若BD=8cm,∠AOD=120°,求边AB的长。
O1200OABCD公平,因为OB=OD = OA=OC生活链接---投圈游戏OABCDOB=OD = OA=OC推论:直角三角形斜边上的中线等于
斜边的一半。
= AC= BD 在 中,∠ABC=900 ,BO是斜边AC上的中线
OB = AC练一练 1. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510 学海 无涯A2.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm2D3.在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.作斜边AB边的中线则 AD=CD= AB∴AC=AD=CD= AB又∵AB=2AC∴⊿ACD是等边三角形∴∠A=60°
∴∠B=30 °练习4.矩形ABCD中,AB=2BC,AE=AB,求∠EBC的度数ABCDE5.设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1________S2.6.已知如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=1200,求∠EAO的度数和∠OEA的度数 。7.已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。2、如图,矩形AEFG和矩形ADCB的大小、形状完全相同,把它们拼成如图所示的L型图案,已知∠FAE=30°,分别求∠1、∠2的度数。 解:依题意可知:
∠FAE=∠DCA=30 °,AF=AC∴∠1=45 °,∴∠2=∠ACF-∠ACD=15 °∴∠DAC=60 °,∴∠FAC=90 °,矩形的定义和性质挑战你的思维 如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢?阅读下面短文矩形的定义和性质
