第8章成对数据的统计分析 单元测试(Word版含答案)
文档属性
| 名称 | 第8章成对数据的统计分析 单元测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 361.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 12:52:18 | ||
图片预览



文档简介
高二数学必修三第8章《成对数据的统计分析》单元测试
一、选择题
1.下列变量之间具有相关关系的是( )
A.利息与利率 B.居民收入与储蓄存款
C.出租车费与行驶的路程 D.某种商品的销售额与销售价格
2.以下四个命题中:
①函数关系是一种确定性关系;
②回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法;
③独立性检验中的统计假设就是假设相关事件A、B相互独立;
④某项测量结果 服从正态分布N(1,a2),且P( ≤5)=0.81,则P(-3≤ <10.31.
以上命题中,真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
3.在一次独立性检验中得到如下列联表:
A1 A2 总计
B1 200 800 1000
B2 180 a 180+a
总计 380 800+a 1180+a
若这两个分类变量A和B没有关系,则a的可能值是( )
A.200 B.720 C.100 D.180
4.通过来判断模拟型拟合的效果,判断原始数据中是否存在可疑数据,这种分析称为( )
A.回归分析 B.独立性检验分析 C.残差分析 D. 散点图分析
5.已知具有线性相关的变量x,y,设其样本点为Pi(xi,yi)(i=1,2,l,6),回归直线方程为=2x+,若++L+=(12,18)(O为坐标原点),则( )
A.-1 B.-6 C.1 D.6
6.利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关,通过随机询问名不同的大学生是否爱好某项运动,利用列联表,由计算可得.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
参照附表,得到的正确结论是( )
A.有以上的把握认为“爱好该项运动与性别无关”
B.有以上的把握认为“爱好该项运动与性别有关”
C.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关”
7.为了考察两个变量和之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为和,已知两人在试验中发现对变量的观测数据的平均值都是,对变量的观测数据的平均值都是,那么下列说法正确的是( )
.和有交点 .与相交,但交点不一定是
.与必定平行 .与必定重合
8.给出下列结论:在回归分析中
(1)可用相关指数R2的值判断模型的拟合效果, R2越大,模型的拟合效果越好;
(2)可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)可用相关系数r的值判断模型的拟合效果,r越大,模型的拟合效果越好;
(4)可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,不正确的是( )
A.(1)(3) B.(2)(3) C.(1)(4) D.(3)(4)
二、多选题
9.已知变量,之间的经验回归方程为,且变量,的数据如表所示,则下列说法正确的是( )
6 8 10 12
6 3 2
A.变量,之间呈正相关关系 B.变量,之间呈负相关关系
C.的值等于5 D.该回归直线必过点
10.某人工智能公司近5年的利润情况如下表所示:
第年 1 2 3 4 5
利润亿元 2 3 4 5 7
10、已知变量与之间具有线性相关关系,设用最小二乘法建立的回归直线方程为,则下列说法正确的是
A.
B.变量与之间的线性相关系数
C.预测该人工智能公司第6年的利润约为7.8亿元
D.该人工智能公司这5年的利润的方差小于2
11.月亮公转与自转的周期大约为30天,阴历是以月相变化为依据.人们根据长时间的观测,统计了月亮出来的时间y(简称“月出时间”,单位:小时)与天数x(x为阴历日数,x,且0≤x≤30)的有关数据,如下表,并且根据表中数据,求得y关于x的线性回归方程为=0.8x+.
x 2 4 7 10 15 22
y 8.1 9.4 12 14.4 18.5 24
其中,阴历22日是分界线,从阴历22日开始月亮就要到第二天(即23日0:00)才升起.则( )
A.样本点的中心为 (10,14.4)
B.=6.8
C.预报月出时间为16时的那天是阴历13日
D.预报阴历27日的月出时间为阴历28日早上4:00
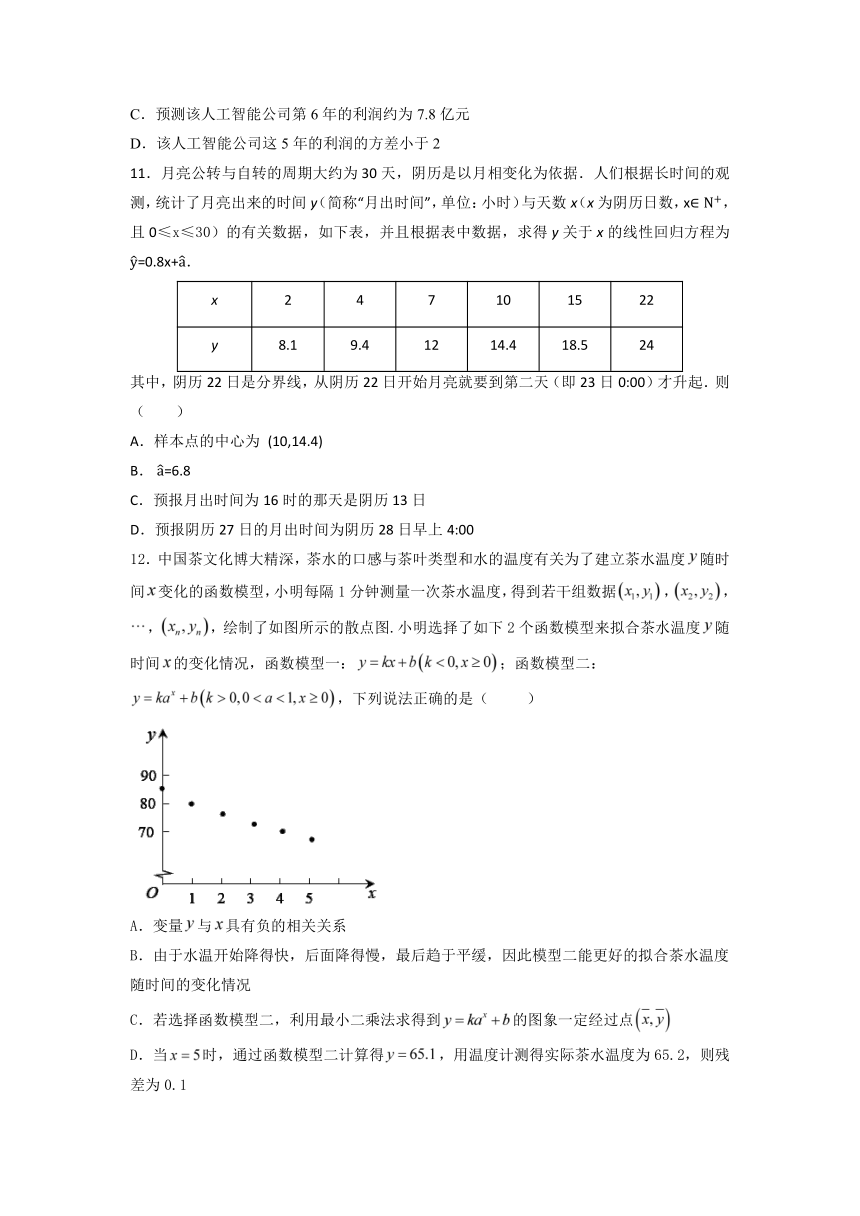
12.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关为了建立茶水温度随时间变化的函数模型,小明每隔1分钟测量一次茶水温度,得到若干组数据,,,,绘制了如图所示的散点图.小明选择了如下2个函数模型来拟合茶水温度随时间的变化情况,函数模型一:;函数模型二:,下列说法正确的是( )
A.变量与具有负的相关关系
B.由于水温开始降得快,后面降得慢,最后趋于平缓,因此模型二能更好的拟合茶水温度随时间的变化情况
C.若选择函数模型二,利用最小二乘法求得到的图象一定经过点
D.当时,通过函数模型二计算得,用温度计测得实际茶水温度为65.2,则残差为0.1
三、填空题
13.对于回归直线方程,当时,的估计值为 .
14.某设备的使用年限x与所支出的维修费用y呈线性相关,部分统计数据如下表:
使用年限x(单位:年) 2.5 3 4 5 5.5
维修费用y(单位:万元) 2 4 5.5 6.5 7
根据上表可得y关于x的回归直线方程为=1.5x+,则=_____,据此模型预测,若使用年限为16年,估计维修费用为__________万元.
15.对两个变量的相关系数r,有下列说法:(1)越大,相关程度越大;(2)越小,相关程度越大;(3)趋近于0时,没有非线性相关系数;(4)越接近于1时,线性相关程度越强,其中正确的是___________.
16.许多因素都会影响贫穷,教育也许是其中之一,在研究这两个因素的关系时收集了美国50个州的成年人受过9年或更少教育的百分比(x)和收入低于官方规定的贫困线的人数占本州人数的百分比()的数据,建立的回归直线方程如下,斜率的估计等于0.8说明 ;成年人受过9年或更少教育的百分比()和收入低于官方的贫困线的人数占本州人数的百分比()之间的相关系数 (填充“大于0”或“小于0”)
四、解答题
17.随着新冠疫情防控进入常态化),人们的生产生活逐步步入正轨.为拉动消费,某市发行2亿元消费券.为了解该消费券使用人群的年龄结构情况,该市随机抽取了50人,对是否使用过消费券的情况进行调查,结果如下表所示,其中年龄低于45岁的人数占总人数的.
年龄(单位:岁) [15,25) [25,35) [35,45) [45,55) [55,65) [65,75)
调查人数 5 m 15 10 n 5
使用消费券人数 5 10 12 7 2 1
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为是否使用消费券与人的年龄有关.
年龄低于45岁的人数 年龄不低于45岁的人数 合计
使用消费券人数
未使用消费券人数
合计
(2)从使用消费券且年龄在[15,25)与[25,35)的人中按分层抽样方法抽取6人,再从这6人中选取2名,记抽取的两人中年龄在[15,25)的人数为X,求X的分布列与数学期望.
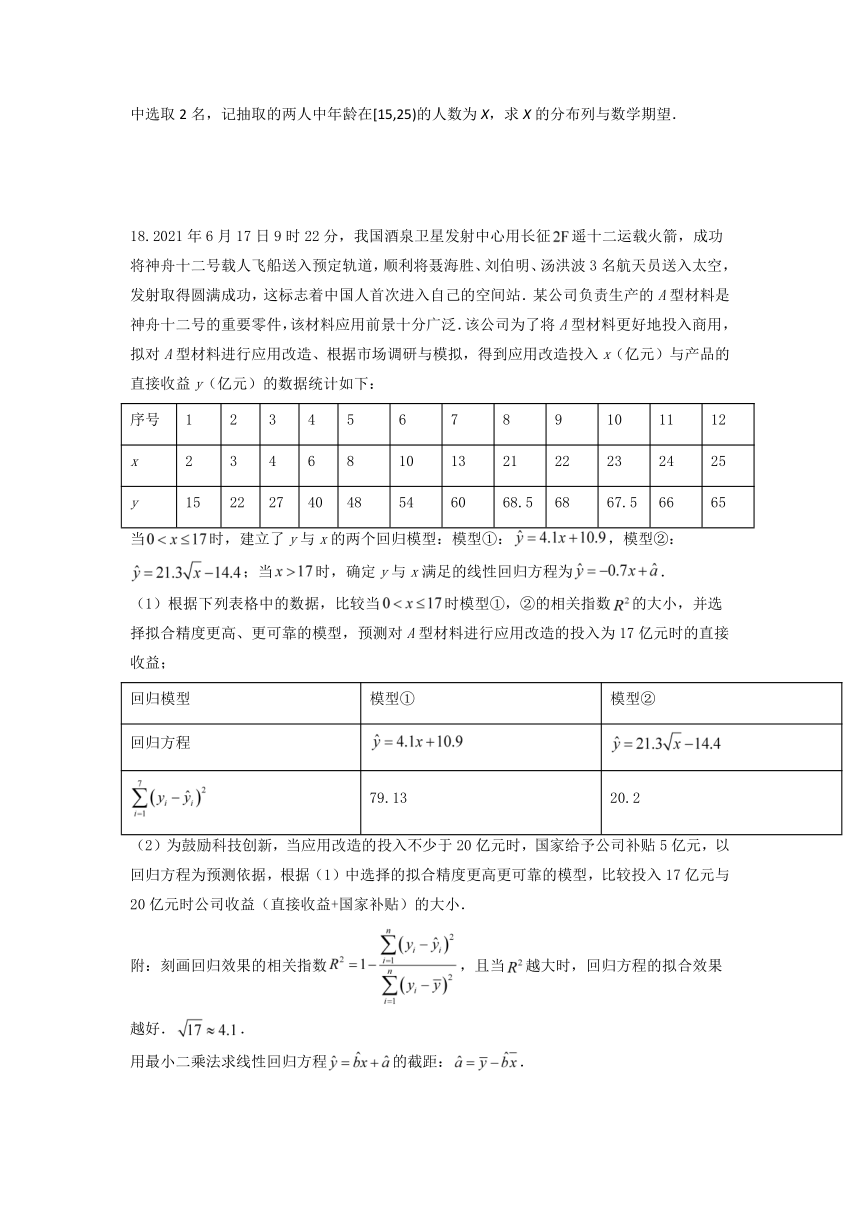
18.2021年6月17日9时22分,我国酒泉卫星发射中心用长征遥十二运载火箭,成功将神舟十二号载人飞船送入预定轨道,顺利将聂海胜、刘伯明、汤洪波3名航天员送入太空,发射取得圆满成功,这标志着中国人首次进入自己的空间站.某公司负责生产的A型材料是神舟十二号的重要零件,该材料应用前景十分广泛.该公司为了将A型材料更好地投入商用,拟对A型材料进行应用改造、根据市场调研与模拟,得到应用改造投入x(亿元)与产品的直接收益y(亿元)的数据统计如下:
序号 1 2 3 4 5 6 7 8 9 10 11 12
x 2 3 4 6 8 10 13 21 22 23 24 25
y 15 22 27 40 48 54 60 68.5 68 67.5 66 65
当时,建立了y与x的两个回归模型:模型①:,模型②:;当时,确定y与x满足的线性回归方程为.
(1)根据下列表格中的数据,比较当时模型①,②的相关指数的大小,并选择拟合精度更高、更可靠的模型,预测对A型材料进行应用改造的投入为17亿元时的直接收益;
回归模型 模型① 模型②
回归方程
79.13 20.2
(2)为鼓励科技创新,当应用改造的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,根据(1)中选择的拟合精度更高更可靠的模型,比较投入17亿元与20亿元时公司收益(直接收益+国家补贴)的大小.
附:刻画回归效果的相关指数,且当越大时,回归方程的拟合效果越好..
用最小二乘法求线性回归方程的截距:.
19.2022年北京冬奥组委发布的《北京2022年冬奥会和冬残奥会经济遗产报告》显示,北京冬奥会已签约45家赞助企业,冬奥会赞助成为一项跨度时间较长的营销方式.为了解该45家赞助企业每天销售额与每天线上销售时间之间的相关关系,某平台对45家赞助企业进行跟踪调查,其中每天线上销售时间不少于8小时的企业有20家,余下的企业中,每天的销售额不足30万元的企业占,统计后得到如下列联表:
销售额不少于30万元 销售额不足30万元 合计
线上销售时间不少于8小时 17 20
线上销售时间不足8小时
合计 45
(1)请完成上面的列联表,并依据的独立性检验,能否认为赞助企业每天的销售额与每天线上销售时间有关;
(2)①按销售额进行分层抽样,在上述赞助企业中抽取5家企业,求销售额不少于30万元和销售额不足30万元的企业数;
②在①条件下,抽取销售额不足30万元的企业时,设抽到每天线上销售时间不少于8小时的企业数是,求的分布列及期望值.
20.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按,,,,分组,绘制频率分布直方图如图所示.试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的列联表,并根据列联表及的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.
(i)用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率;
(ii)以(i)中确定的概率作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记个人注射2次疫苗后产生抗体的数量为随机变量.试验后统计数据显示,当时,取最大值,求参加人体接种试验的人数及.
参考公式:(其中为样本容量)
参考数据:
0.50 0.40 0.25 0.15 0.100 0.050 0.025
0.455 0.708 1.323 2.072 2.706 3.841 5.024
22.为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 1 2 3 4 5 6 7 8
零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次序 9 10 11 12 13 14 15 16
零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得,,,,其中为抽取的第i个零件的尺寸,.
(1)求的相关系数,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本的相关系数,.
一、选择题
1-8.B D B C A B A B
二、多选题
9. B C D 10. A C 11. A D 12. A B D
三、填空题
13.390
14.-1,23
15. (1) (4)
16.一个地区受过9年或更少教育的百分比每增加1%,收入低于官方规定的贫困线的人数占本州人数的百分比将增加0.8%左右;大于0
四、解答题
17.(1)列联表见解析,有99%的把握认为是否使用消费券与人的年龄有关;(2)分布列见解析,数学期望为.
18. (1)模型②拟合精度更高、更可靠,亿;(2)投入17亿元比投入20亿元时收益小.
19.解:(1)每天线上销售时间不少于8小时的企业有20家,
每天线上销售时间不足8小时的企业有家,其中每天销售额不足30万元的企业有家,
故列联表如下:
销售额不少于30万元 销售额不足30万元 合计
线上销售时间不少于8小时 17 3 20
线上销售时间不足8小时 10 15 25
合计 27 18 45
,
依据的独立性检验,能认为赞助企业每天的销售额与每天线上销售时间有关.
(2)①销售额不少于30万元的企业数:,
销售额不足30万元的企业数:.
②由题意可得,所有可能取值为0,1,2,
,,,
故的分布列为:
0 1 2
故.
20. 【答案】(1)列联表答案见解析,认为注射疫苗后小白鼠产生抗体与指标值不小于60有关;(2)(i);(ii)当接种人数为n=99时,;当n=100时,.
【解析】(1)由频率分布直方图,知200只小白鼠按指标值分布为:
在内有(只);
在内有(只);
在内有(只);
在内有(只);
在内有(只).
由题意,有抗体且指标值小于60的有50只;而指标值小于60的小白鼠共有(只),所以指标值小于60且没有抗体的小白鼠有20只,同理,指标值不小于60且没有抗体的小白鼠有20只,故列联表如下:
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
零假设为:注射疫苗后小白鼠产生抗体与指标值不小于60无关联.
根据列联表中数据,得.
根据的独立性检验,推断不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)(i)令事件“小白鼠第一次注射疫苗产生抗体”,事件“小白鼠第二次注射疫苗产生抗体”,事件“小白鼠注射2次疫苗后产生抗体”.
记事件A,B,C发生的概率分别为,,,
则,,.
所以一只小白鼠注射2次疫苗后产生抗体的概率.
(ii)由题意,知随机变量,().
因为最大,
所以,
解得,因为是整数,所以或,所以接受接种试验的人数为99或100.
①当接种人数为99时,;
②当接种人数为100时,.
22.【解析】(1)由样本数据得的相关系数为
.
由于,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
(2)(i)由于,由样本数据可以看出抽取的第13个零件的尺寸在以外,因此需对当天的生产过程进行检查.
(ii)剔除离群值,即第13个数据,剩下数据的平均数为,这条生产线当天生产的零件尺寸的均值的估计值为10.02.
,
剔除第13个数据,剩下数据的样本方差为,
这条生产线当天生产的零件尺寸的标准差的估计值为.
一、选择题
1.下列变量之间具有相关关系的是( )
A.利息与利率 B.居民收入与储蓄存款
C.出租车费与行驶的路程 D.某种商品的销售额与销售价格
2.以下四个命题中:
①函数关系是一种确定性关系;
②回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法;
③独立性检验中的统计假设就是假设相关事件A、B相互独立;
④某项测量结果 服从正态分布N(1,a2),且P( ≤5)=0.81,则P(-3≤ <10.31.
以上命题中,真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
3.在一次独立性检验中得到如下列联表:
A1 A2 总计
B1 200 800 1000
B2 180 a 180+a
总计 380 800+a 1180+a
若这两个分类变量A和B没有关系,则a的可能值是( )
A.200 B.720 C.100 D.180
4.通过来判断模拟型拟合的效果,判断原始数据中是否存在可疑数据,这种分析称为( )
A.回归分析 B.独立性检验分析 C.残差分析 D. 散点图分析
5.已知具有线性相关的变量x,y,设其样本点为Pi(xi,yi)(i=1,2,l,6),回归直线方程为=2x+,若++L+=(12,18)(O为坐标原点),则( )
A.-1 B.-6 C.1 D.6
6.利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关,通过随机询问名不同的大学生是否爱好某项运动,利用列联表,由计算可得.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
参照附表,得到的正确结论是( )
A.有以上的把握认为“爱好该项运动与性别无关”
B.有以上的把握认为“爱好该项运动与性别有关”
C.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关”
7.为了考察两个变量和之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为和,已知两人在试验中发现对变量的观测数据的平均值都是,对变量的观测数据的平均值都是,那么下列说法正确的是( )
.和有交点 .与相交,但交点不一定是
.与必定平行 .与必定重合
8.给出下列结论:在回归分析中
(1)可用相关指数R2的值判断模型的拟合效果, R2越大,模型的拟合效果越好;
(2)可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)可用相关系数r的值判断模型的拟合效果,r越大,模型的拟合效果越好;
(4)可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,不正确的是( )
A.(1)(3) B.(2)(3) C.(1)(4) D.(3)(4)
二、多选题
9.已知变量,之间的经验回归方程为,且变量,的数据如表所示,则下列说法正确的是( )
6 8 10 12
6 3 2
A.变量,之间呈正相关关系 B.变量,之间呈负相关关系
C.的值等于5 D.该回归直线必过点
10.某人工智能公司近5年的利润情况如下表所示:
第年 1 2 3 4 5
利润亿元 2 3 4 5 7
10、已知变量与之间具有线性相关关系,设用最小二乘法建立的回归直线方程为,则下列说法正确的是
A.
B.变量与之间的线性相关系数
C.预测该人工智能公司第6年的利润约为7.8亿元
D.该人工智能公司这5年的利润的方差小于2
11.月亮公转与自转的周期大约为30天,阴历是以月相变化为依据.人们根据长时间的观测,统计了月亮出来的时间y(简称“月出时间”,单位:小时)与天数x(x为阴历日数,x,且0≤x≤30)的有关数据,如下表,并且根据表中数据,求得y关于x的线性回归方程为=0.8x+.
x 2 4 7 10 15 22
y 8.1 9.4 12 14.4 18.5 24
其中,阴历22日是分界线,从阴历22日开始月亮就要到第二天(即23日0:00)才升起.则( )
A.样本点的中心为 (10,14.4)
B.=6.8
C.预报月出时间为16时的那天是阴历13日
D.预报阴历27日的月出时间为阴历28日早上4:00
12.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关为了建立茶水温度随时间变化的函数模型,小明每隔1分钟测量一次茶水温度,得到若干组数据,,,,绘制了如图所示的散点图.小明选择了如下2个函数模型来拟合茶水温度随时间的变化情况,函数模型一:;函数模型二:,下列说法正确的是( )
A.变量与具有负的相关关系
B.由于水温开始降得快,后面降得慢,最后趋于平缓,因此模型二能更好的拟合茶水温度随时间的变化情况
C.若选择函数模型二,利用最小二乘法求得到的图象一定经过点
D.当时,通过函数模型二计算得,用温度计测得实际茶水温度为65.2,则残差为0.1
三、填空题
13.对于回归直线方程,当时,的估计值为 .
14.某设备的使用年限x与所支出的维修费用y呈线性相关,部分统计数据如下表:
使用年限x(单位:年) 2.5 3 4 5 5.5
维修费用y(单位:万元) 2 4 5.5 6.5 7
根据上表可得y关于x的回归直线方程为=1.5x+,则=_____,据此模型预测,若使用年限为16年,估计维修费用为__________万元.
15.对两个变量的相关系数r,有下列说法:(1)越大,相关程度越大;(2)越小,相关程度越大;(3)趋近于0时,没有非线性相关系数;(4)越接近于1时,线性相关程度越强,其中正确的是___________.
16.许多因素都会影响贫穷,教育也许是其中之一,在研究这两个因素的关系时收集了美国50个州的成年人受过9年或更少教育的百分比(x)和收入低于官方规定的贫困线的人数占本州人数的百分比()的数据,建立的回归直线方程如下,斜率的估计等于0.8说明 ;成年人受过9年或更少教育的百分比()和收入低于官方的贫困线的人数占本州人数的百分比()之间的相关系数 (填充“大于0”或“小于0”)
四、解答题
17.随着新冠疫情防控进入常态化),人们的生产生活逐步步入正轨.为拉动消费,某市发行2亿元消费券.为了解该消费券使用人群的年龄结构情况,该市随机抽取了50人,对是否使用过消费券的情况进行调查,结果如下表所示,其中年龄低于45岁的人数占总人数的.
年龄(单位:岁) [15,25) [25,35) [35,45) [45,55) [55,65) [65,75)
调查人数 5 m 15 10 n 5
使用消费券人数 5 10 12 7 2 1
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为是否使用消费券与人的年龄有关.
年龄低于45岁的人数 年龄不低于45岁的人数 合计
使用消费券人数
未使用消费券人数
合计
(2)从使用消费券且年龄在[15,25)与[25,35)的人中按分层抽样方法抽取6人,再从这6人中选取2名,记抽取的两人中年龄在[15,25)的人数为X,求X的分布列与数学期望.
18.2021年6月17日9时22分,我国酒泉卫星发射中心用长征遥十二运载火箭,成功将神舟十二号载人飞船送入预定轨道,顺利将聂海胜、刘伯明、汤洪波3名航天员送入太空,发射取得圆满成功,这标志着中国人首次进入自己的空间站.某公司负责生产的A型材料是神舟十二号的重要零件,该材料应用前景十分广泛.该公司为了将A型材料更好地投入商用,拟对A型材料进行应用改造、根据市场调研与模拟,得到应用改造投入x(亿元)与产品的直接收益y(亿元)的数据统计如下:
序号 1 2 3 4 5 6 7 8 9 10 11 12
x 2 3 4 6 8 10 13 21 22 23 24 25
y 15 22 27 40 48 54 60 68.5 68 67.5 66 65
当时,建立了y与x的两个回归模型:模型①:,模型②:;当时,确定y与x满足的线性回归方程为.
(1)根据下列表格中的数据,比较当时模型①,②的相关指数的大小,并选择拟合精度更高、更可靠的模型,预测对A型材料进行应用改造的投入为17亿元时的直接收益;
回归模型 模型① 模型②
回归方程
79.13 20.2
(2)为鼓励科技创新,当应用改造的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,根据(1)中选择的拟合精度更高更可靠的模型,比较投入17亿元与20亿元时公司收益(直接收益+国家补贴)的大小.
附:刻画回归效果的相关指数,且当越大时,回归方程的拟合效果越好..
用最小二乘法求线性回归方程的截距:.
19.2022年北京冬奥组委发布的《北京2022年冬奥会和冬残奥会经济遗产报告》显示,北京冬奥会已签约45家赞助企业,冬奥会赞助成为一项跨度时间较长的营销方式.为了解该45家赞助企业每天销售额与每天线上销售时间之间的相关关系,某平台对45家赞助企业进行跟踪调查,其中每天线上销售时间不少于8小时的企业有20家,余下的企业中,每天的销售额不足30万元的企业占,统计后得到如下列联表:
销售额不少于30万元 销售额不足30万元 合计
线上销售时间不少于8小时 17 20
线上销售时间不足8小时
合计 45
(1)请完成上面的列联表,并依据的独立性检验,能否认为赞助企业每天的销售额与每天线上销售时间有关;
(2)①按销售额进行分层抽样,在上述赞助企业中抽取5家企业,求销售额不少于30万元和销售额不足30万元的企业数;
②在①条件下,抽取销售额不足30万元的企业时,设抽到每天线上销售时间不少于8小时的企业数是,求的分布列及期望值.
20.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按,,,,分组,绘制频率分布直方图如图所示.试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的列联表,并根据列联表及的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.
(i)用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率;
(ii)以(i)中确定的概率作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记个人注射2次疫苗后产生抗体的数量为随机变量.试验后统计数据显示,当时,取最大值,求参加人体接种试验的人数及.
参考公式:(其中为样本容量)
参考数据:
0.50 0.40 0.25 0.15 0.100 0.050 0.025
0.455 0.708 1.323 2.072 2.706 3.841 5.024
22.为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 1 2 3 4 5 6 7 8
零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次序 9 10 11 12 13 14 15 16
零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得,,,,其中为抽取的第i个零件的尺寸,.
(1)求的相关系数,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本的相关系数,.
一、选择题
1-8.B D B C A B A B
二、多选题
9. B C D 10. A C 11. A D 12. A B D
三、填空题
13.390
14.-1,23
15. (1) (4)
16.一个地区受过9年或更少教育的百分比每增加1%,收入低于官方规定的贫困线的人数占本州人数的百分比将增加0.8%左右;大于0
四、解答题
17.(1)列联表见解析,有99%的把握认为是否使用消费券与人的年龄有关;(2)分布列见解析,数学期望为.
18. (1)模型②拟合精度更高、更可靠,亿;(2)投入17亿元比投入20亿元时收益小.
19.解:(1)每天线上销售时间不少于8小时的企业有20家,
每天线上销售时间不足8小时的企业有家,其中每天销售额不足30万元的企业有家,
故列联表如下:
销售额不少于30万元 销售额不足30万元 合计
线上销售时间不少于8小时 17 3 20
线上销售时间不足8小时 10 15 25
合计 27 18 45
,
依据的独立性检验,能认为赞助企业每天的销售额与每天线上销售时间有关.
(2)①销售额不少于30万元的企业数:,
销售额不足30万元的企业数:.
②由题意可得,所有可能取值为0,1,2,
,,,
故的分布列为:
0 1 2
故.
20. 【答案】(1)列联表答案见解析,认为注射疫苗后小白鼠产生抗体与指标值不小于60有关;(2)(i);(ii)当接种人数为n=99时,;当n=100时,.
【解析】(1)由频率分布直方图,知200只小白鼠按指标值分布为:
在内有(只);
在内有(只);
在内有(只);
在内有(只);
在内有(只).
由题意,有抗体且指标值小于60的有50只;而指标值小于60的小白鼠共有(只),所以指标值小于60且没有抗体的小白鼠有20只,同理,指标值不小于60且没有抗体的小白鼠有20只,故列联表如下:
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
零假设为:注射疫苗后小白鼠产生抗体与指标值不小于60无关联.
根据列联表中数据,得.
根据的独立性检验,推断不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)(i)令事件“小白鼠第一次注射疫苗产生抗体”,事件“小白鼠第二次注射疫苗产生抗体”,事件“小白鼠注射2次疫苗后产生抗体”.
记事件A,B,C发生的概率分别为,,,
则,,.
所以一只小白鼠注射2次疫苗后产生抗体的概率.
(ii)由题意,知随机变量,().
因为最大,
所以,
解得,因为是整数,所以或,所以接受接种试验的人数为99或100.
①当接种人数为99时,;
②当接种人数为100时,.
22.【解析】(1)由样本数据得的相关系数为
.
由于,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
(2)(i)由于,由样本数据可以看出抽取的第13个零件的尺寸在以外,因此需对当天的生产过程进行检查.
(ii)剔除离群值,即第13个数据,剩下数据的平均数为,这条生产线当天生产的零件尺寸的均值的估计值为10.02.
,
剔除第13个数据,剩下数据的样本方差为,
这条生产线当天生产的零件尺寸的标准差的估计值为.
