冀教版数学七年级下册 第十一章 数学活动 拼图与分解因式 (2)教案(表格式)
文档属性
| 名称 | 冀教版数学七年级下册 第十一章 数学活动 拼图与分解因式 (2)教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 39.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 11:18:29 | ||
图片预览

文档简介
教师活动 学生活动 设计意图 预设
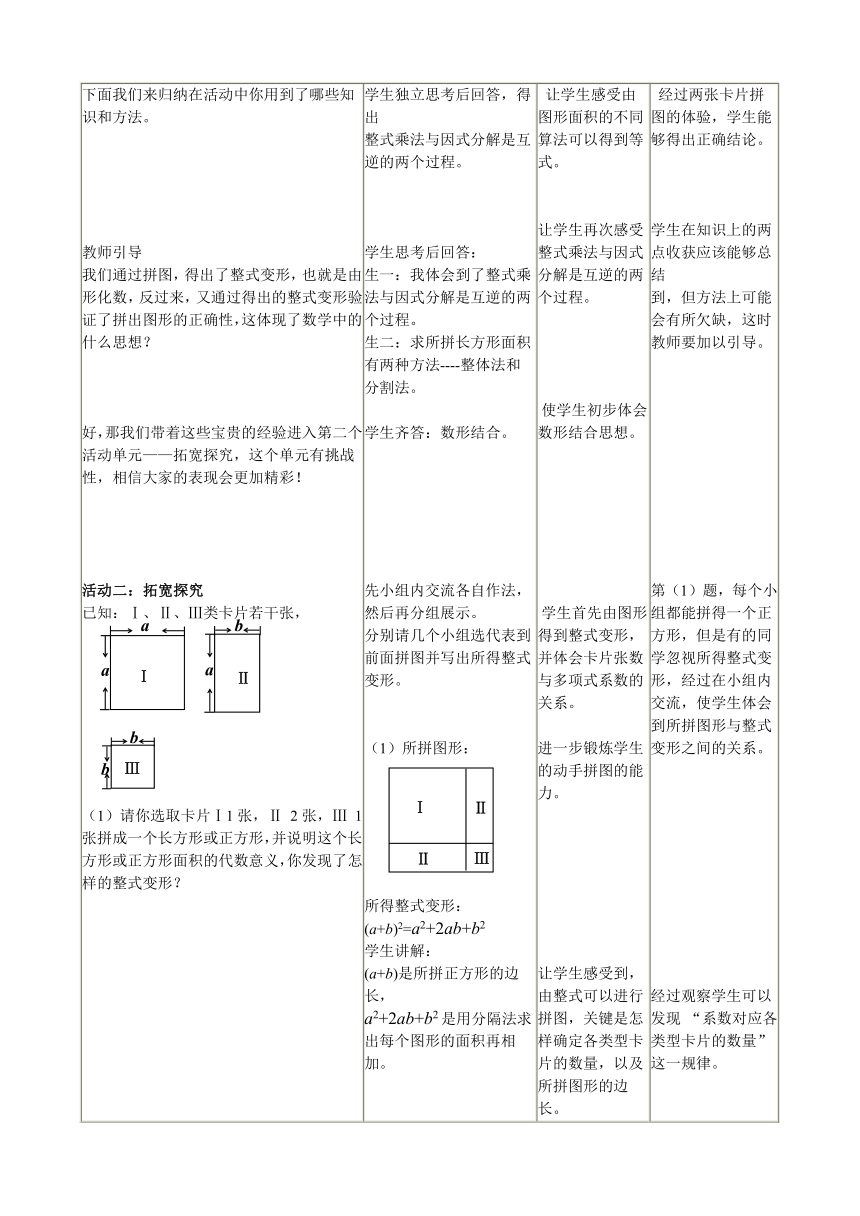
(一)情境引入: 这是同学们玩过的拼图游戏,把各种形状的图形拼成了一个长方形,同学们想玩吗? (二)新课教学 活动一:快乐体验 利用如下的长方形卡片拼成更大的长方形. (
n
m
Ⅰ
) (
m
a
Ⅱ
) (
b
n
Ⅲ
) 探究: (1)你任意选用两张长方形卡片拼成一个大的长方形,并用两种方法求出你拼出的大长方形的面积. 从中可以看出求所拼 大长方形面积有两种方法: 一种是整体法,利用长乘以宽;一种是分割法,分成两部分计算面积再求和。 所得整式变形哪种是整式乘法,哪种是因式分解?两者之间的关系又是怎样的? 下面我们来归纳在活动中你用到了哪些知识和方法。 教师引导 我们通过拼图,得出了整式变形,也就是由形化数,反过来,又通过得出的整式变形验证了拼出图形的正确性,这体现了数学中的什么思想? 好,那我们带着这些宝贵的经验进入第二个活动单元——拓宽探究,这个单元有挑战性,相信大家的表现会更加精彩! 活动二:拓宽探究 (
b
a
Ⅱ
) (
a
a
Ⅰ
)已知:Ⅰ、Ⅱ、Ⅲ类卡片若干张, (
b
b
Ⅲ
) (1)请你选取卡片Ⅰ1张,Ⅱ 2张,Ⅲ 1张拼成一个长方形或正方形,并说明这个长方形或正方形面积的代数意义,你发现了怎样的整式变形? 2)按照下面给出的整式选取卡片,拼接成长方形或正方形,并利用它们的面积说明相应的整式变形. ① ; ② . 教师引导: 结合图形想一想(a+b) (2a+b)中的每个因式的几何意义是什么? 怎样得出每种卡片的张数? ? 教师引导:通过所得整式变形,想一想,如果不进行拼图你能否得出图形的边长? 牛刀小试 1、用Ⅰ、Ⅱ、Ⅲ卡片若干张,拼成一个长为 (2a+b),宽为 (a+2b)的矩形,不用拼图,需要Ⅰ类卡片 _______张, Ⅱ类卡片_______张,Ⅲ类_______张. 回音壁 本节课我学会了…… 使我感触最深的是…… 我感到最困难的是…… 学生引起浓厚兴趣,观察并思考。 小组内交流各自拼图方法和所得整式变形。 小组展示: (1)有两种拼法: (
n
Ⅰ
m
a
Ⅱ
) 方法一: 所得整式变形: m(a+n)=ma+mn或 ma+mn= m(a+n) 方法二: (
m
Ⅰ
b
Ⅲ
n
) 所得整式变形: n(m+b)=nm+nb或 nm+nb=n(m+b) 学生结合所拼图形讲解所得整式变形的几何意义。 学生独立思考后回答,得出 整式乘法与因式分解是互逆的两个过程。 学生思考后回答: 生一:我体会到了整式乘法与因式分解是互逆的两个过程。 生二:求所拼长方形面积有两种方法----整体法和分割法。 学生齐答:数形结合。 先小组内交流各自作法,然后再分组展示。 分别请几个小组选代表到前面拼图并写出所得整式变形。 (1)所拼图形: (
Ⅰ
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
) 所得整式变形: (a+b)2=a2+2ab+b2 学生讲解: (a+b)是所拼正方形的边长, a2+2ab+b2是用分隔法求出每个图形的面积再相加。 (2) ①所拼图形: (
Ⅰ
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅰ
Ⅱ
Ⅰ
) 所得整式变形: (a+b) (2a+b) =2a2+3ab+b2 学生讲解: (a+b) (2a+b)是用整体法求面积,将这一幅图看作成一个长方形面积表示成长乘以宽; 2a2+3ab+b2是用分割法求面积,将这一幅图中一个小正方形,三个长方形和两个正方形的面积相加。 这其中a2表示一个小正方形的面积3ab表示三个长方形的面积2b2表示两个大正方形的面积。 ②所拼图形: (
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅰ
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
) 所得整式变形: a2+4ab+4b2= (a+2b)2 学生独立思考后回答: 根据因式分解的结果也可以得出所拼图形的边长。 请几位学生拼图后上台展示。引导学生自己介绍拼出的长方形的长与宽,以及得到的等式。 学生小组讨论后回答: 生一:完全平方的多项式可以用拼图来说明。 生二:可以分解成两个因式乘积的二次三项式可以用拼图来说明。 请学生总结。 学生讲解: 1、 (2a+b) (a+2b) = 2a2+5ab+2b2 根据系数,可知需要Ⅰ类卡片2张,Ⅱ类卡片5张,Ⅲ类2张。 学生畅所欲言。 创设有利于学生思考的问题情景,激发学习的探究欲望。 让学生通过动手操作初步体会拼图,锻炼学生的动手拼图的能力,由所得整式变形回忆前面学过的整式乘法与因式分解。 让学生感受由图形面积的不同算法可以得到等式 让学生感受整式乘法与因式分解是互逆的两个过程。 让学生感受由图形面积的不同算法可以得到等式。 让学生再次感受整式乘法与因式分解是互逆的两个过程。 使学生初步体会数形结合思想。 学生首先由图形得到整式变形,并体会卡片张数与多项式系数的关系。 进一步锻炼学生的动手拼图的能力。 让学生感受到,由整式可以进行拼图,关键是怎样确定各类型卡片的数量,以及所拼图形的边长。 让学生感受到拼图可以帮助进行分解因式 反之,分解因式也可以帮助确定图形的边长。 初步感受不能因式分解的多项式根据它不能拼出长方形。 让学生感受到因式分解可以指导拼图。 渗透数形结合的数学思想。 由同学们熟悉的拼图游戏,开始本节课的游戏主线。 学生可能会说出表示整式乘法的等式或是因式分解的等式。 但是整式乘法的等式要熟悉一些,关于因式分解的等式需要引导。 学生在板书时要求他将表示整式乘法的等式写一边,表示因式分解的写一边。方便后面的教学。 学生还是会对于表示整式乘法的等式熟悉一些,对于表示因分解的等式还是要提醒,这就要求在深入学生活动时要全面。 经过两张卡片拼图的体验,学生能够得出正确结论。 学生在知识上的两点收获应该能够总结 到,但方法上可能会有所欠缺,这时教师要加以引导。 第(1)题,每个小组都能拼得一个正方形,但是有的同学忽视所得整式变形,经过在小组内交流,使学生体会到所拼图形与整式变形之间的关系。 经过观察学生可以发现 “系数对应各类型卡片的数量”这一规律。 学生独立拼图有困难,主要是不知怎样选取卡片的张数,需要教师的引导。 学生可能出现的方法: 1、由(2a+b)(a+b)可知,长方形的长是(2a+b),宽是(a+b),所以就在一边放2个边长是a的一个边长是b的,另一边放1个边长是a的一个边长是b的; 2、把(2a+b)(a+b)乘出来,得到2a2+3ab+b2,可知三种卡片的张数。 在前面总结规律的基础上,同学们能够准确的选择卡片并进行拼图。 仅一个例题,学生的感受还不是很深刻,但是课堂时间的限制,没有更多的时间,可以将课堂上的内容延伸到课后让学生去自己体会。 许多学生的第一反应是动手拼图。
(一)情境引入: 这是同学们玩过的拼图游戏,把各种形状的图形拼成了一个长方形,同学们想玩吗? (二)新课教学 活动一:快乐体验 利用如下的长方形卡片拼成更大的长方形. (
n
m
Ⅰ
) (
m
a
Ⅱ
) (
b
n
Ⅲ
) 探究: (1)你任意选用两张长方形卡片拼成一个大的长方形,并用两种方法求出你拼出的大长方形的面积. 从中可以看出求所拼 大长方形面积有两种方法: 一种是整体法,利用长乘以宽;一种是分割法,分成两部分计算面积再求和。 所得整式变形哪种是整式乘法,哪种是因式分解?两者之间的关系又是怎样的? 下面我们来归纳在活动中你用到了哪些知识和方法。 教师引导 我们通过拼图,得出了整式变形,也就是由形化数,反过来,又通过得出的整式变形验证了拼出图形的正确性,这体现了数学中的什么思想? 好,那我们带着这些宝贵的经验进入第二个活动单元——拓宽探究,这个单元有挑战性,相信大家的表现会更加精彩! 活动二:拓宽探究 (
b
a
Ⅱ
) (
a
a
Ⅰ
)已知:Ⅰ、Ⅱ、Ⅲ类卡片若干张, (
b
b
Ⅲ
) (1)请你选取卡片Ⅰ1张,Ⅱ 2张,Ⅲ 1张拼成一个长方形或正方形,并说明这个长方形或正方形面积的代数意义,你发现了怎样的整式变形? 2)按照下面给出的整式选取卡片,拼接成长方形或正方形,并利用它们的面积说明相应的整式变形. ① ; ② . 教师引导: 结合图形想一想(a+b) (2a+b)中的每个因式的几何意义是什么? 怎样得出每种卡片的张数? ? 教师引导:通过所得整式变形,想一想,如果不进行拼图你能否得出图形的边长? 牛刀小试 1、用Ⅰ、Ⅱ、Ⅲ卡片若干张,拼成一个长为 (2a+b),宽为 (a+2b)的矩形,不用拼图,需要Ⅰ类卡片 _______张, Ⅱ类卡片_______张,Ⅲ类_______张. 回音壁 本节课我学会了…… 使我感触最深的是…… 我感到最困难的是…… 学生引起浓厚兴趣,观察并思考。 小组内交流各自拼图方法和所得整式变形。 小组展示: (1)有两种拼法: (
n
Ⅰ
m
a
Ⅱ
) 方法一: 所得整式变形: m(a+n)=ma+mn或 ma+mn= m(a+n) 方法二: (
m
Ⅰ
b
Ⅲ
n
) 所得整式变形: n(m+b)=nm+nb或 nm+nb=n(m+b) 学生结合所拼图形讲解所得整式变形的几何意义。 学生独立思考后回答,得出 整式乘法与因式分解是互逆的两个过程。 学生思考后回答: 生一:我体会到了整式乘法与因式分解是互逆的两个过程。 生二:求所拼长方形面积有两种方法----整体法和分割法。 学生齐答:数形结合。 先小组内交流各自作法,然后再分组展示。 分别请几个小组选代表到前面拼图并写出所得整式变形。 (1)所拼图形: (
Ⅰ
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
) 所得整式变形: (a+b)2=a2+2ab+b2 学生讲解: (a+b)是所拼正方形的边长, a2+2ab+b2是用分隔法求出每个图形的面积再相加。 (2) ①所拼图形: (
Ⅰ
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅰ
Ⅱ
Ⅰ
) 所得整式变形: (a+b) (2a+b) =2a2+3ab+b2 学生讲解: (a+b) (2a+b)是用整体法求面积,将这一幅图看作成一个长方形面积表示成长乘以宽; 2a2+3ab+b2是用分割法求面积,将这一幅图中一个小正方形,三个长方形和两个正方形的面积相加。 这其中a2表示一个小正方形的面积3ab表示三个长方形的面积2b2表示两个大正方形的面积。 ②所拼图形: (
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅰ
Ⅱ
Ⅰ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
Ⅲ
Ⅱ
Ⅰ
) 所得整式变形: a2+4ab+4b2= (a+2b)2 学生独立思考后回答: 根据因式分解的结果也可以得出所拼图形的边长。 请几位学生拼图后上台展示。引导学生自己介绍拼出的长方形的长与宽,以及得到的等式。 学生小组讨论后回答: 生一:完全平方的多项式可以用拼图来说明。 生二:可以分解成两个因式乘积的二次三项式可以用拼图来说明。 请学生总结。 学生讲解: 1、 (2a+b) (a+2b) = 2a2+5ab+2b2 根据系数,可知需要Ⅰ类卡片2张,Ⅱ类卡片5张,Ⅲ类2张。 学生畅所欲言。 创设有利于学生思考的问题情景,激发学习的探究欲望。 让学生通过动手操作初步体会拼图,锻炼学生的动手拼图的能力,由所得整式变形回忆前面学过的整式乘法与因式分解。 让学生感受由图形面积的不同算法可以得到等式 让学生感受整式乘法与因式分解是互逆的两个过程。 让学生感受由图形面积的不同算法可以得到等式。 让学生再次感受整式乘法与因式分解是互逆的两个过程。 使学生初步体会数形结合思想。 学生首先由图形得到整式变形,并体会卡片张数与多项式系数的关系。 进一步锻炼学生的动手拼图的能力。 让学生感受到,由整式可以进行拼图,关键是怎样确定各类型卡片的数量,以及所拼图形的边长。 让学生感受到拼图可以帮助进行分解因式 反之,分解因式也可以帮助确定图形的边长。 初步感受不能因式分解的多项式根据它不能拼出长方形。 让学生感受到因式分解可以指导拼图。 渗透数形结合的数学思想。 由同学们熟悉的拼图游戏,开始本节课的游戏主线。 学生可能会说出表示整式乘法的等式或是因式分解的等式。 但是整式乘法的等式要熟悉一些,关于因式分解的等式需要引导。 学生在板书时要求他将表示整式乘法的等式写一边,表示因式分解的写一边。方便后面的教学。 学生还是会对于表示整式乘法的等式熟悉一些,对于表示因分解的等式还是要提醒,这就要求在深入学生活动时要全面。 经过两张卡片拼图的体验,学生能够得出正确结论。 学生在知识上的两点收获应该能够总结 到,但方法上可能会有所欠缺,这时教师要加以引导。 第(1)题,每个小组都能拼得一个正方形,但是有的同学忽视所得整式变形,经过在小组内交流,使学生体会到所拼图形与整式变形之间的关系。 经过观察学生可以发现 “系数对应各类型卡片的数量”这一规律。 学生独立拼图有困难,主要是不知怎样选取卡片的张数,需要教师的引导。 学生可能出现的方法: 1、由(2a+b)(a+b)可知,长方形的长是(2a+b),宽是(a+b),所以就在一边放2个边长是a的一个边长是b的,另一边放1个边长是a的一个边长是b的; 2、把(2a+b)(a+b)乘出来,得到2a2+3ab+b2,可知三种卡片的张数。 在前面总结规律的基础上,同学们能够准确的选择卡片并进行拼图。 仅一个例题,学生的感受还不是很深刻,但是课堂时间的限制,没有更多的时间,可以将课堂上的内容延伸到课后让学生去自己体会。 许多学生的第一反应是动手拼图。
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
