小学数学苏教版四年级下三角形的内角和课件(共18张PPT)
文档属性
| 名称 | 小学数学苏教版四年级下三角形的内角和课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 11:18:25 | ||
图片预览


文档简介
(共18张PPT)
三角形的内角和
义务教育教科书苏教版小学数学四年级下册第七单元
1.请你准备好铅笔、橡皮、练习本、三角尺、量角器用于课堂学习。
2.上课中需要思考或练习的时候,请按下“暂停按钮”,完成后再继续观看学习下面的内容。
课前准备
1
2
3
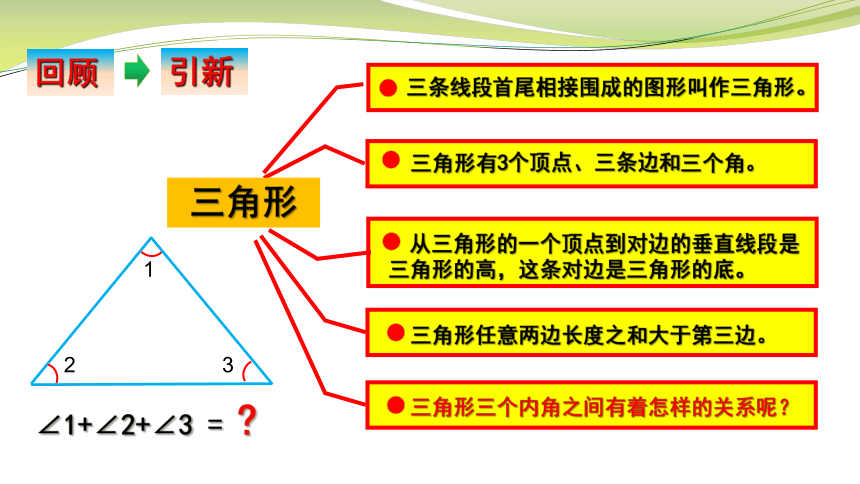
三条线段首尾相接围成的图形叫作三角形。
三角形有3个顶点、三条边和三个角。
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
三角形任意两边长度之和大于第三边。
三角形
三角形三个内角之间有着怎样的关系呢?
∠1+∠2+∠3 =
回顾
引新
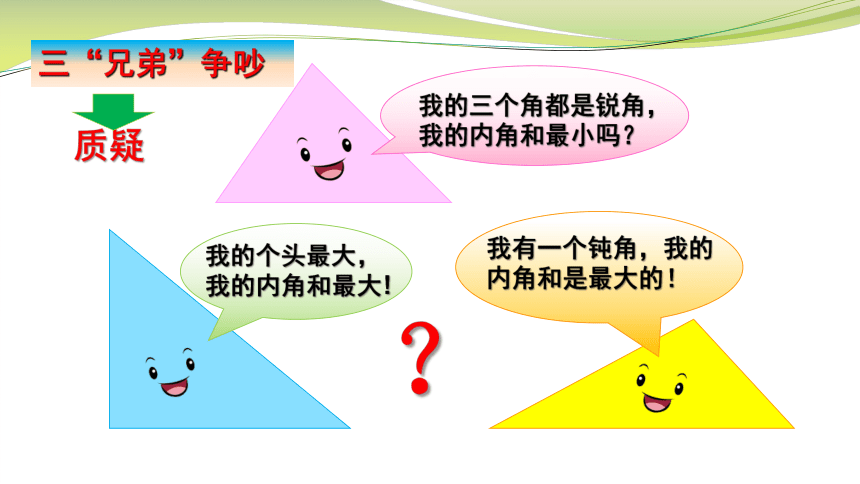
我有一个钝角,我的内角和是最大的!
我的个头最大,我的内角和最大!
我的三个角都是锐角,我的内角和最小吗?
三“兄弟”争吵
?
质疑
30°
60°
90°
45°
90°
45°
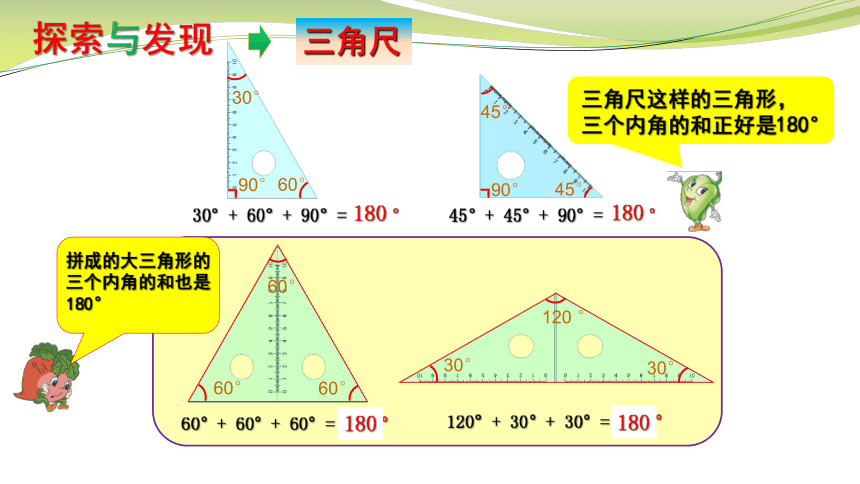
30°+ 60°+ 90°= ? °
45°+ 45°+ 90°= ? °
60°+ 60°+ 60°= °
120°+ 30°+ 30°= °
60°
60°
60°
30°
30°
120 °
三角尺
探索与发现
180
180
180
180
三角尺这样的三角形,
三个内角的和正好是180°
拼成的大三角形的
三个内角的和也是
180°
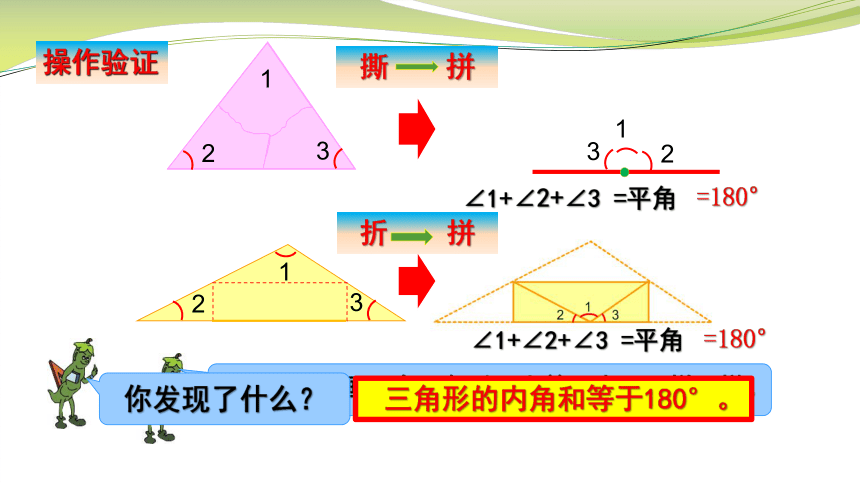
操作验证
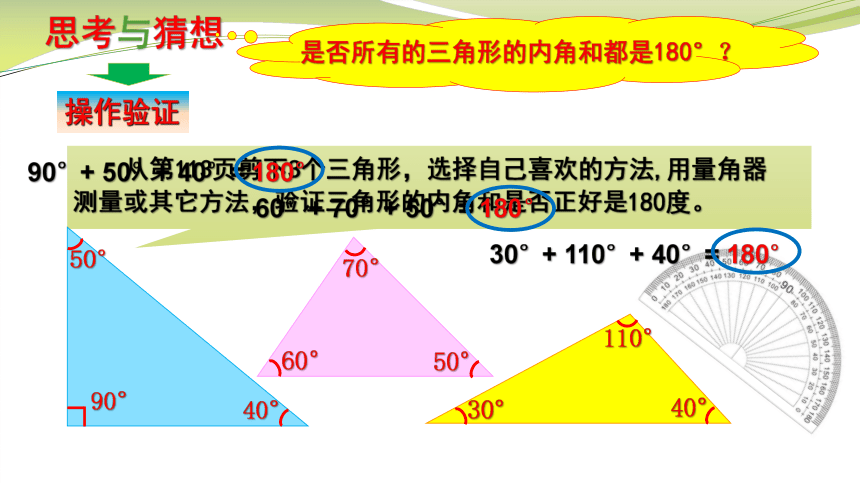
思考与猜想
是否所有的三角形的内角和都是180°?
从第113页剪下3个三角形,选择自己喜欢的方法,用量角器测量或其它方法,验证三角形的内角和是否正好是180度。
90°+ 50°+ 40°= 180°
60°+ 70°+ 50°= 180°
30°+ 110°+ 40°= 180°
50°
40°
90°
70°
50°
60°
40°
30°
110°
1
2
3
3
3
1
2
1
2
自己再任意画一个三角形,先剪下来,再拼一拼。
撕 拼
折 拼
∠1+∠2+∠3 =平角
=180°
∠1+∠2+∠3 =平角
=180°
操作验证
你发现了什么?
三角形的内角和等于180°。
我有一个钝角,我的内角和是最大的!
我的个头最大,我的内角和最大!
我的三个角都是锐角,我的内角和最小吗?
三“兄弟”争吵
三角形的内角和相等,都是180°
?
解疑
法国数学家 布莱士 帕斯卡
.
360 ÷2=180
。
。
……
……
180 ×2
。
。
-180 =180
。
你知道吗?
三角形的内角和等于180°。
40。
80°
60°
90°
35°
110°
55°
40°
30°
三角形中一个未知角的度数是多少?
?
?
?
想一想,算一算
三角形的内角和等于180°。
180°-40°-60°= 80°
180°-35°-55°= 90°
180°-30°-40°= 110°
180°-(40°+60°)= 80°
180°-(35°+55°)= 90°
180°-(30°+40°)= 110°
通过刚才的观察和计算,你有什么发现?
55°
?
想一想,算一算
180°- 90°- 55°= 35°
90°
90°
90°- 55°= 35°
如果三角形中有一个内角是直角,那么另外两个角的和是90°。
180°- (90°+ 55°)= 35°
如果已知三角形两个内角的度数,要求第三个内角是多少度,只要用内角和180°去减去两个已知角的度数。
∠1+∠2+∠3 =180 °
∠1= 180 °- (∠2+∠3)
∠2= 180 °- (∠1+∠3)
∠3= 180 °- (∠1+∠2)
1
2
∠1+∠2 =90 °
∠1= 90 °- ∠2
∠2= 90 °- ∠1
体会与收获
1
2
3
想一想,做一做
正方形
( )形
( )形
内角和( )°
内角和( )°
内角和( )°
三角
三角
360
180
180
90 °× 4 = 360°
用一张正方形纸折一折,填一填。
被遮住的两个内角会是什么角?
根据内角和是180 ° ,一个三角形中最多只有一个钝角或一个直角,
至少有两个角是锐角。
下面的三角形被一张纸遮住了一部分,露出的这个内角是个锐角。
自我挑战
回顾总结
通过今天的学习和研究,你有哪些收获?
通过观察、猜想、测量、剪拼和折叠等方法,
发现了三角形的内角和是180°。
如果已知三角形两个内角的度数,要求第三个角是多少度,只要用三角形的内角和180°去减去两个已知角的度数。
1
2
3
三条线段首尾相接围成的图形叫作三角形。
三角形有3个顶点、三条边和三个角。
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
三角形任意两边长度之和大于第三边。
三角形
三角形三个内角之间有什么关系呢?
∠1+∠2+∠3 =
180°
的和是180°
三角形……
回顾总结
你能利用今天所学的知识想办法知道四边形、五边形和六边形等的内角和吗?
课后思考
内角和180°
内角和 ?
内角和 ?
内角和 ?
三角形
四边形
五边形
六边形
再见!
三角形的内角和
义务教育教科书苏教版小学数学四年级下册第七单元
1.请你准备好铅笔、橡皮、练习本、三角尺、量角器用于课堂学习。
2.上课中需要思考或练习的时候,请按下“暂停按钮”,完成后再继续观看学习下面的内容。
课前准备
1
2
3
三条线段首尾相接围成的图形叫作三角形。
三角形有3个顶点、三条边和三个角。
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
三角形任意两边长度之和大于第三边。
三角形
三角形三个内角之间有着怎样的关系呢?
∠1+∠2+∠3 =
回顾
引新
我有一个钝角,我的内角和是最大的!
我的个头最大,我的内角和最大!
我的三个角都是锐角,我的内角和最小吗?
三“兄弟”争吵
?
质疑
30°
60°
90°
45°
90°
45°
30°+ 60°+ 90°= ? °
45°+ 45°+ 90°= ? °
60°+ 60°+ 60°= °
120°+ 30°+ 30°= °
60°
60°
60°
30°
30°
120 °
三角尺
探索与发现
180
180
180
180
三角尺这样的三角形,
三个内角的和正好是180°
拼成的大三角形的
三个内角的和也是
180°
操作验证
思考与猜想
是否所有的三角形的内角和都是180°?
从第113页剪下3个三角形,选择自己喜欢的方法,用量角器测量或其它方法,验证三角形的内角和是否正好是180度。
90°+ 50°+ 40°= 180°
60°+ 70°+ 50°= 180°
30°+ 110°+ 40°= 180°
50°
40°
90°
70°
50°
60°
40°
30°
110°
1
2
3
3
3
1
2
1
2
自己再任意画一个三角形,先剪下来,再拼一拼。
撕 拼
折 拼
∠1+∠2+∠3 =平角
=180°
∠1+∠2+∠3 =平角
=180°
操作验证
你发现了什么?
三角形的内角和等于180°。
我有一个钝角,我的内角和是最大的!
我的个头最大,我的内角和最大!
我的三个角都是锐角,我的内角和最小吗?
三“兄弟”争吵
三角形的内角和相等,都是180°
?
解疑
法国数学家 布莱士 帕斯卡
.
360 ÷2=180
。
。
……
……
180 ×2
。
。
-180 =180
。
你知道吗?
三角形的内角和等于180°。
40。
80°
60°
90°
35°
110°
55°
40°
30°
三角形中一个未知角的度数是多少?
?
?
?
想一想,算一算
三角形的内角和等于180°。
180°-40°-60°= 80°
180°-35°-55°= 90°
180°-30°-40°= 110°
180°-(40°+60°)= 80°
180°-(35°+55°)= 90°
180°-(30°+40°)= 110°
通过刚才的观察和计算,你有什么发现?
55°
?
想一想,算一算
180°- 90°- 55°= 35°
90°
90°
90°- 55°= 35°
如果三角形中有一个内角是直角,那么另外两个角的和是90°。
180°- (90°+ 55°)= 35°
如果已知三角形两个内角的度数,要求第三个内角是多少度,只要用内角和180°去减去两个已知角的度数。
∠1+∠2+∠3 =180 °
∠1= 180 °- (∠2+∠3)
∠2= 180 °- (∠1+∠3)
∠3= 180 °- (∠1+∠2)
1
2
∠1+∠2 =90 °
∠1= 90 °- ∠2
∠2= 90 °- ∠1
体会与收获
1
2
3
想一想,做一做
正方形
( )形
( )形
内角和( )°
内角和( )°
内角和( )°
三角
三角
360
180
180
90 °× 4 = 360°
用一张正方形纸折一折,填一填。
被遮住的两个内角会是什么角?
根据内角和是180 ° ,一个三角形中最多只有一个钝角或一个直角,
至少有两个角是锐角。
下面的三角形被一张纸遮住了一部分,露出的这个内角是个锐角。
自我挑战
回顾总结
通过今天的学习和研究,你有哪些收获?
通过观察、猜想、测量、剪拼和折叠等方法,
发现了三角形的内角和是180°。
如果已知三角形两个内角的度数,要求第三个角是多少度,只要用三角形的内角和180°去减去两个已知角的度数。
1
2
3
三条线段首尾相接围成的图形叫作三角形。
三角形有3个顶点、三条边和三个角。
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
三角形任意两边长度之和大于第三边。
三角形
三角形三个内角之间有什么关系呢?
∠1+∠2+∠3 =
180°
的和是180°
三角形……
回顾总结
你能利用今天所学的知识想办法知道四边形、五边形和六边形等的内角和吗?
课后思考
内角和180°
内角和 ?
内角和 ?
内角和 ?
三角形
四边形
五边形
六边形
再见!
