1.3带电粒子在综合场中的运动独讲讲义
文档属性
| 名称 | 1.3带电粒子在综合场中的运动独讲讲义 |

|
|
| 格式 | zip | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-03 00:00:00 | ||
图片预览


文档简介
带电粒子在综合场中的运动独讲
一 带电粒子在叠加场中的运动
【基本知识点】
1.带电粒子在叠加场中运动的基本性质
(1)匀速直线运动:若带电粒子所受合外力为零,它将处于静止或匀速直线运动状态;
(2)匀速圆周运动:若带电粒子所受合外力只充当向心力,它将做匀速圆周运动;
(3)匀变速运动:若带电粒子所受合外力恒定,它将做匀变速运动;
(4)非匀变速运动:若带电粒子所受合外力不恒定,它将做非匀变速运动。
2.带电体所受重力、静电力与洛伦兹力的性质各不相同,做功情况也不同,应予以区别。
大小 方向 做功特点 做功大小
重力 mg 竖直向下 与路径无关,只与始、末位置的高度差有关 W=mgh
静电力 qE 与电场方向相同或相反 与路径无关,只与始、末位置间的电势差有关 W=qU
洛伦兹力 v∥B,则f=0 v⊥B,则f=qvB 由左手定则判定 永不做功 0
3.带电粒子在复合场中运动问题的处理方法:
(1)首先要弄清复合场的组成。其次,要正确地对带电粒子进行受力分析和运动过程分析。在进行受力分析时要注意洛伦兹力方向的判定方法——左手定则。在分析运动过程时,要特别注意洛伦兹力的特点——方向始终和运动方向垂直,永不做功。最后,选择合适的动力学方程进行求解。
(2)带电粒子在复合场中的运动问题是电磁学知识和力学知识的结合,分析方法和力学问题的分析方法基本相同,不同之处是多了静电力和洛伦兹力。因此,带电粒子在复合场中的运动问题要注意电场和磁场对带电粒子的作用特点,如静电力做功与路径无关,洛伦兹力方向始终和运动速度方向垂直且永不做功等。
【例题分析】
例1 如图所示,在竖直平面内建立直角坐标系xOy,其第一象限存在着正交的匀强电场和匀强磁场,电场强度的方向水平向右,磁感应强度的方向垂直纸面向里。一带电荷量为+q、质量为m的微粒从坐标原点出发,沿与x轴正方向的夹角为45°的初速度方向进入复合场中,正好做直线运动,当微粒运动到A(l,l)时,电场方向突然变为竖直向上(不计电场变化的时间),微粒继续运动一段时间后,正好垂直于y轴穿出复合场。不计一切阻力,求:
(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)微粒在复合场中的运动时间t。
例2 如图所示,空间中存在着水平向右的匀强电场,电场强度大小E=5 N/C,同时存在着水平方向的匀强磁场,其方向与电场方向垂直,磁感应强度大小B=0.5 T.有一带正电的小球,质量m=1×10-6 kg,电荷量q=2×10-6 C,正以速度v在图示的竖直面内做匀速直线运动,当经过P点时撤掉磁场(不考虑磁场消失引起的电磁感应现象)取g=10 m/s2,求:
(1)小球做匀速直线运动的速度v的大小和方向;
(2)从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t.
二 带电粒子在组合场中的运动
【基本知识点】
1.组合场:电场与磁场各位于一定的区域内,并不重叠,一般为两场相邻或在同一区域电场、磁场交替出现。
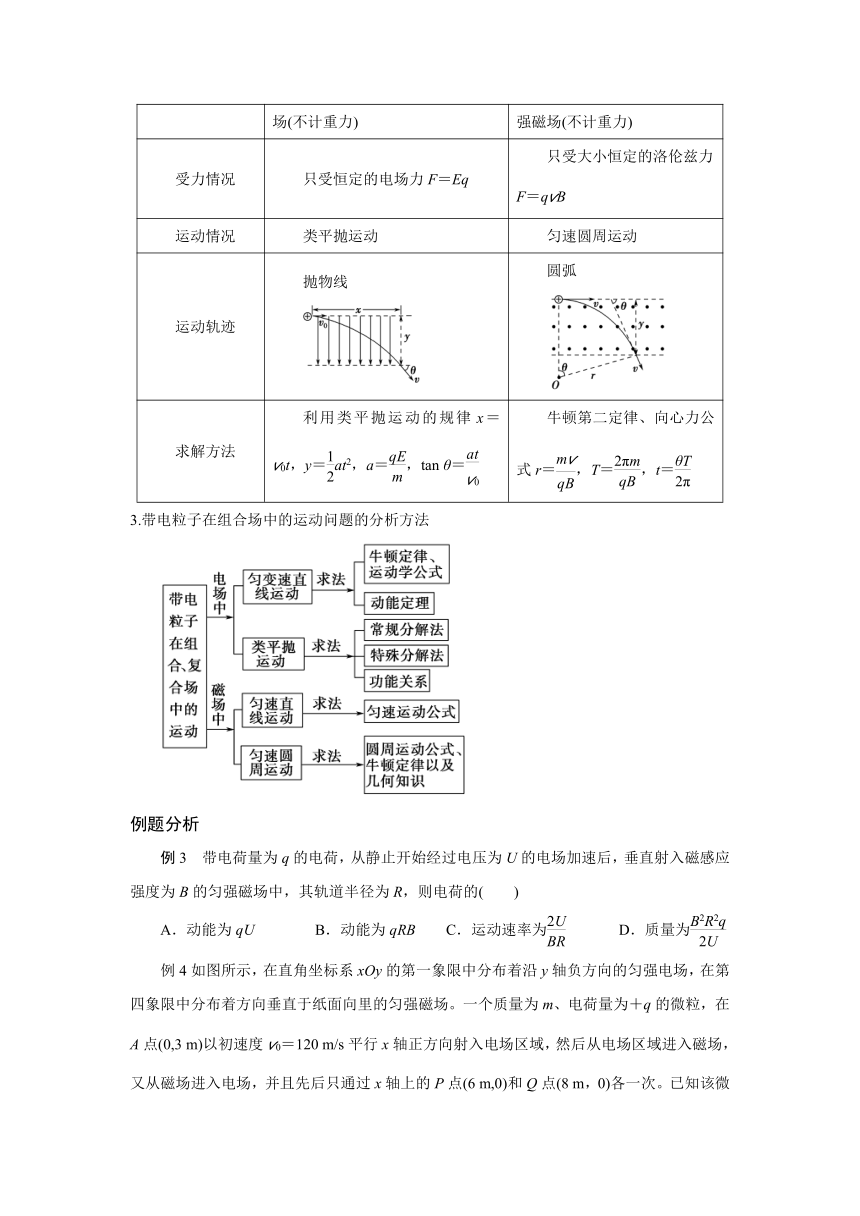
2.“磁偏转”和“电偏转”的比较
电偏转 磁偏转
偏转条件 带电粒子以v⊥E进入匀强电场(不计重力) 带电粒子以v⊥B进入匀强磁场(不计重力)
受力情况 只受恒定的电场力F=Eq 只受大小恒定的洛伦兹力F=qvB
运动情况 类平抛运动 匀速圆周运动
运动轨迹 抛物线 圆弧
求解方法 利用类平抛运动的规律x=v0t,y=at2,a=,tan θ= 牛顿第二定律、向心力公式r=,T=,t=
3.带电粒子在组合场中的运动问题的分析方法
例题分析
例3 带电荷量为q的电荷,从静止开始经过电压为U的电场加速后,垂直射入磁感应强度为B的匀强磁场中,其轨道半径为R,则电荷的( )
A.动能为qU B.动能为qRB C.运动速率为 D.质量为
例4如图所示,在直角坐标系xOy的第一象限中分布着沿y轴负方向的匀强电场,在第四象限中分布着方向垂直于纸面向里的匀强磁场。一个质量为m、电荷量为+q的微粒,在A点(0,3 m)以初速度v0=120 m/s平行x轴正方向射入电场区域,然后从电场区域进入磁场,又从磁场进入电场,并且先后只通过x轴上的P点(6 m,0)和Q点(8 m,0)各一次。已知该微粒的比荷为=102 C/kg,微粒重力不计,
(1)求微粒从A到P所经历的时间和加速度的大小;
(2)求出微粒到达P点时速度方向与x轴正方向的夹角,并画出带电微粒在电场和磁场中由A至Q的运动轨迹;
(3)求电场强度E和磁感应强度B的大小。
【知识小结】
带电粒子在综合场中的运动独讲答案
例1解析 (1)微粒在到达A(l,l)之前做匀速直线运动,受力分析如图:
根据平衡条件,有:qE=mg解得:E=。
(2)根据平衡条件,有:qvB=mg,
电场方向变化后,微粒所受重力与电场力平衡,微粒在洛伦兹力作用下做匀速圆周运动,轨迹如图:
根据牛顿第二定律,有:qvB=m,
由几何关系可得:r=l,联立解得:v=,B=。
(3)微粒做匀速直线运动的时间为:t1==,
做圆周运动的时间为:t2==π ,
在复合场中运动时间为:t=t1+t2=。
答案 (1) (2) (3)
例2解析 (1)小球匀速直线运动时受力如图,其所受的三个力在同一平面内,
合力为零,有qvB=①
代入数据解得v=20 m/s②
速度v的方向与电场E的方向之间的夹角满足tan θ=③
代入数据解得tan θ= θ=60°④
(2)解法一 撤去磁场,小球在重力与电场力的合力作用下做类平抛运动,如图所示,设其加速度为a,有a=⑤
设撤去磁场后小球在初速度方向上的分位移为x,有x=vt⑥
设小球在重力与电场力的合力方向上分位移为y,有y=at2⑦
tan θ=⑧
联立④⑤⑥⑦⑧式,代入数据解得t=2 s=3.5 s⑨
解法二 撤去磁场后,由于电场力垂直于竖直方向,它对竖直方向的分运动没有影响,以P点为坐标原点,竖直向上为正方向,小球在竖直方向上做匀减速运动,其初速度为
vy=vsin θ⑩
若使小球再次穿过P点所在的电场线,仅需小球的竖直方向上分位移为零,则有vyt-gt2=0
联立⑩ 式,代入数据解得t=2 s=3.5 s
答案 (1)20 m/s 与电场方向成60°角斜向上(2)3.5 s
例3解析 电荷在电场中被加速,设加速后电荷的动能为Ek,由动能定理得:Ek-0=qU,所以Ek=qU,选项A正确;设电荷的质量为m、速率为v,电荷做圆周运动的半径R====,所以v=,选项C正确;将v=代入R=整理得m=,选项D正确.
答案 ACD
例4解析 (1)微粒从平行x轴正方向射入电场区域,由A到P做类平抛运动,微粒在x轴正方向做匀速直线运动
由x=v0t,得t==0.05 s
微粒沿y轴负方向做初速度为零的匀加速直线运动,
由y=at2得a=2.4×103 m/s2。
(2)vy=at,tan α==1,所以α=45°
轨迹如图
(3)由qE=ma,得E=24 N/C
设微粒从P点进入磁场以速度v做匀速圆周运动,
v=v0=120 m/s
由几何关系可知r= m,由qvB=m得B==1.2 T。
答案 (1)0.05 s 2.4×103 m/s2(2)45° 见解析图 (3)24 N/C 1.2 T
一 带电粒子在叠加场中的运动
【基本知识点】
1.带电粒子在叠加场中运动的基本性质
(1)匀速直线运动:若带电粒子所受合外力为零,它将处于静止或匀速直线运动状态;
(2)匀速圆周运动:若带电粒子所受合外力只充当向心力,它将做匀速圆周运动;
(3)匀变速运动:若带电粒子所受合外力恒定,它将做匀变速运动;
(4)非匀变速运动:若带电粒子所受合外力不恒定,它将做非匀变速运动。
2.带电体所受重力、静电力与洛伦兹力的性质各不相同,做功情况也不同,应予以区别。
大小 方向 做功特点 做功大小
重力 mg 竖直向下 与路径无关,只与始、末位置的高度差有关 W=mgh
静电力 qE 与电场方向相同或相反 与路径无关,只与始、末位置间的电势差有关 W=qU
洛伦兹力 v∥B,则f=0 v⊥B,则f=qvB 由左手定则判定 永不做功 0
3.带电粒子在复合场中运动问题的处理方法:
(1)首先要弄清复合场的组成。其次,要正确地对带电粒子进行受力分析和运动过程分析。在进行受力分析时要注意洛伦兹力方向的判定方法——左手定则。在分析运动过程时,要特别注意洛伦兹力的特点——方向始终和运动方向垂直,永不做功。最后,选择合适的动力学方程进行求解。
(2)带电粒子在复合场中的运动问题是电磁学知识和力学知识的结合,分析方法和力学问题的分析方法基本相同,不同之处是多了静电力和洛伦兹力。因此,带电粒子在复合场中的运动问题要注意电场和磁场对带电粒子的作用特点,如静电力做功与路径无关,洛伦兹力方向始终和运动速度方向垂直且永不做功等。
【例题分析】
例1 如图所示,在竖直平面内建立直角坐标系xOy,其第一象限存在着正交的匀强电场和匀强磁场,电场强度的方向水平向右,磁感应强度的方向垂直纸面向里。一带电荷量为+q、质量为m的微粒从坐标原点出发,沿与x轴正方向的夹角为45°的初速度方向进入复合场中,正好做直线运动,当微粒运动到A(l,l)时,电场方向突然变为竖直向上(不计电场变化的时间),微粒继续运动一段时间后,正好垂直于y轴穿出复合场。不计一切阻力,求:
(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)微粒在复合场中的运动时间t。
例2 如图所示,空间中存在着水平向右的匀强电场,电场强度大小E=5 N/C,同时存在着水平方向的匀强磁场,其方向与电场方向垂直,磁感应强度大小B=0.5 T.有一带正电的小球,质量m=1×10-6 kg,电荷量q=2×10-6 C,正以速度v在图示的竖直面内做匀速直线运动,当经过P点时撤掉磁场(不考虑磁场消失引起的电磁感应现象)取g=10 m/s2,求:
(1)小球做匀速直线运动的速度v的大小和方向;
(2)从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t.
二 带电粒子在组合场中的运动
【基本知识点】
1.组合场:电场与磁场各位于一定的区域内,并不重叠,一般为两场相邻或在同一区域电场、磁场交替出现。
2.“磁偏转”和“电偏转”的比较
电偏转 磁偏转
偏转条件 带电粒子以v⊥E进入匀强电场(不计重力) 带电粒子以v⊥B进入匀强磁场(不计重力)
受力情况 只受恒定的电场力F=Eq 只受大小恒定的洛伦兹力F=qvB
运动情况 类平抛运动 匀速圆周运动
运动轨迹 抛物线 圆弧
求解方法 利用类平抛运动的规律x=v0t,y=at2,a=,tan θ= 牛顿第二定律、向心力公式r=,T=,t=
3.带电粒子在组合场中的运动问题的分析方法
例题分析
例3 带电荷量为q的电荷,从静止开始经过电压为U的电场加速后,垂直射入磁感应强度为B的匀强磁场中,其轨道半径为R,则电荷的( )
A.动能为qU B.动能为qRB C.运动速率为 D.质量为
例4如图所示,在直角坐标系xOy的第一象限中分布着沿y轴负方向的匀强电场,在第四象限中分布着方向垂直于纸面向里的匀强磁场。一个质量为m、电荷量为+q的微粒,在A点(0,3 m)以初速度v0=120 m/s平行x轴正方向射入电场区域,然后从电场区域进入磁场,又从磁场进入电场,并且先后只通过x轴上的P点(6 m,0)和Q点(8 m,0)各一次。已知该微粒的比荷为=102 C/kg,微粒重力不计,
(1)求微粒从A到P所经历的时间和加速度的大小;
(2)求出微粒到达P点时速度方向与x轴正方向的夹角,并画出带电微粒在电场和磁场中由A至Q的运动轨迹;
(3)求电场强度E和磁感应强度B的大小。
【知识小结】
带电粒子在综合场中的运动独讲答案
例1解析 (1)微粒在到达A(l,l)之前做匀速直线运动,受力分析如图:
根据平衡条件,有:qE=mg解得:E=。
(2)根据平衡条件,有:qvB=mg,
电场方向变化后,微粒所受重力与电场力平衡,微粒在洛伦兹力作用下做匀速圆周运动,轨迹如图:
根据牛顿第二定律,有:qvB=m,
由几何关系可得:r=l,联立解得:v=,B=。
(3)微粒做匀速直线运动的时间为:t1==,
做圆周运动的时间为:t2==π ,
在复合场中运动时间为:t=t1+t2=。
答案 (1) (2) (3)
例2解析 (1)小球匀速直线运动时受力如图,其所受的三个力在同一平面内,
合力为零,有qvB=①
代入数据解得v=20 m/s②
速度v的方向与电场E的方向之间的夹角满足tan θ=③
代入数据解得tan θ= θ=60°④
(2)解法一 撤去磁场,小球在重力与电场力的合力作用下做类平抛运动,如图所示,设其加速度为a,有a=⑤
设撤去磁场后小球在初速度方向上的分位移为x,有x=vt⑥
设小球在重力与电场力的合力方向上分位移为y,有y=at2⑦
tan θ=⑧
联立④⑤⑥⑦⑧式,代入数据解得t=2 s=3.5 s⑨
解法二 撤去磁场后,由于电场力垂直于竖直方向,它对竖直方向的分运动没有影响,以P点为坐标原点,竖直向上为正方向,小球在竖直方向上做匀减速运动,其初速度为
vy=vsin θ⑩
若使小球再次穿过P点所在的电场线,仅需小球的竖直方向上分位移为零,则有vyt-gt2=0
联立⑩ 式,代入数据解得t=2 s=3.5 s
答案 (1)20 m/s 与电场方向成60°角斜向上(2)3.5 s
例3解析 电荷在电场中被加速,设加速后电荷的动能为Ek,由动能定理得:Ek-0=qU,所以Ek=qU,选项A正确;设电荷的质量为m、速率为v,电荷做圆周运动的半径R====,所以v=,选项C正确;将v=代入R=整理得m=,选项D正确.
答案 ACD
例4解析 (1)微粒从平行x轴正方向射入电场区域,由A到P做类平抛运动,微粒在x轴正方向做匀速直线运动
由x=v0t,得t==0.05 s
微粒沿y轴负方向做初速度为零的匀加速直线运动,
由y=at2得a=2.4×103 m/s2。
(2)vy=at,tan α==1,所以α=45°
轨迹如图
(3)由qE=ma,得E=24 N/C
设微粒从P点进入磁场以速度v做匀速圆周运动,
v=v0=120 m/s
由几何关系可知r= m,由qvB=m得B==1.2 T。
答案 (1)0.05 s 2.4×103 m/s2(2)45° 见解析图 (3)24 N/C 1.2 T
