冀教版数学七年级下册 9.2 三角形内角和定理课件(共20张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 9.2 三角形内角和定理课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 485.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 16:41:25 | ||
图片预览





文档简介
(共20张PPT)
三角形内角和定理
1、了解并掌握三角形内角和定理的内容。
2、明确通过作辅助线来解决几何问题的思路。
4、学习并掌握从猜想到验证的几何研究方法。
3、学会简单利用三角形内角和定理计算三角形的内角度数。
学习目标
重点
1、能从多角度用多种方法证明三角形的内角和定理。
2、会在求证中添加合适的辅助线。
难点
三角形内角和定理的运用。
证明命题的一般步骤:
1、理解题意,分清命题的条件(已知),结论(求证)。
2、根据题意,画出图形。
3、结合图形,用符号语言写出已知和求证。
4、分析题意,探索证明思路。
5、依据思路,用数学符号和数学语言条理清晰地写出证明过程。
6、检查表达过程是否正确完善。
复习
A
B
C
演示
1
2
3
三角形的三个内角和是多少
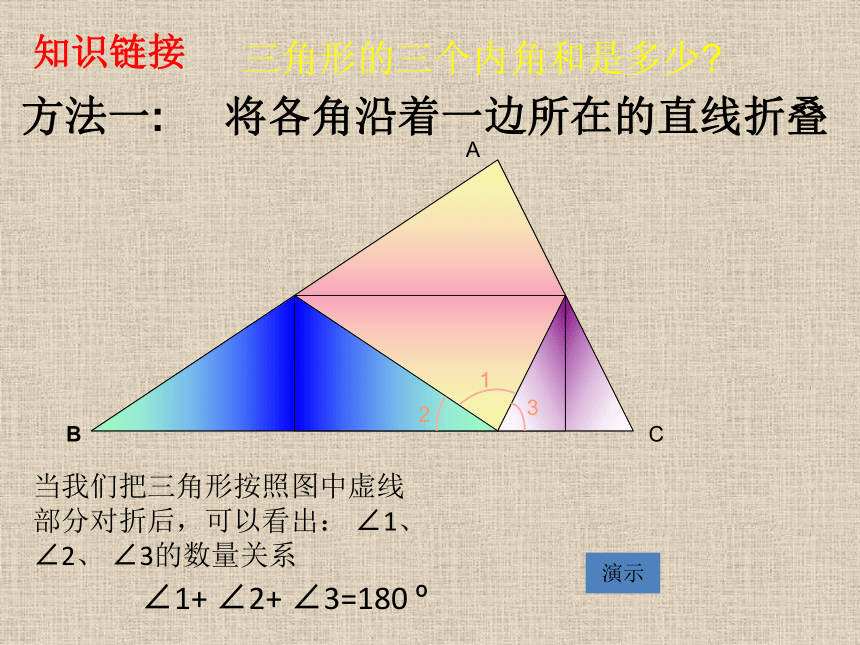
方法一: 将各角沿着一边所在的直线折叠
知识链接
当我们把三角形按照图中虚线部分对折后,可以看出: ∠1、 ∠2、 ∠3的数量关系
∠1+ ∠2+ ∠3=180
A
B
C
A
B
验证
方法二:
在小学,我们通过剪拼发现了三角形的三个内角和等于180
1
2
3
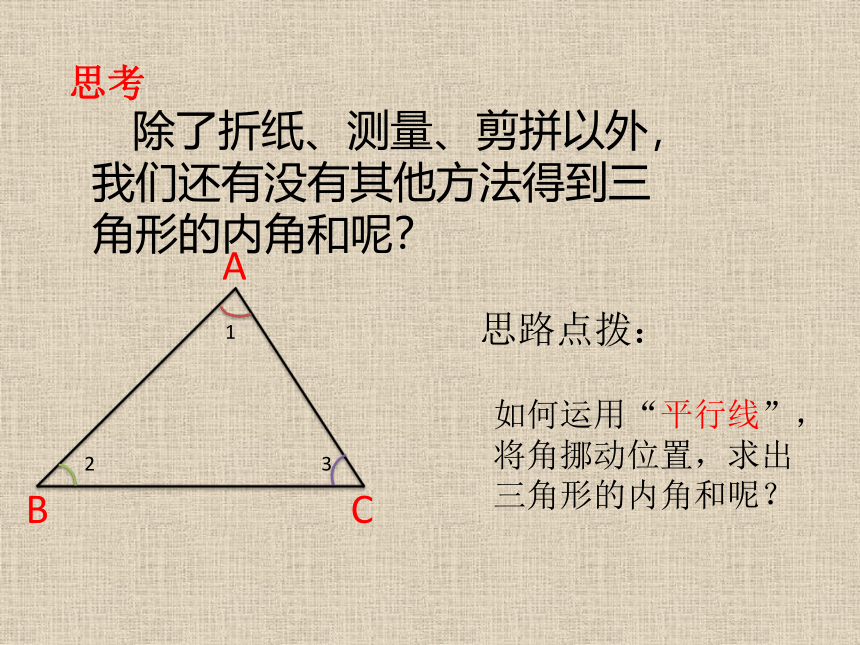
除了折纸、测量、剪拼以外,我们还有没有其他方法得到三角形的内角和呢?
A
B
C
思路点拨:
如何运用“平行线”,将角挪动位置,求出三角形的内角和呢?
思考
1
2
3
1
2
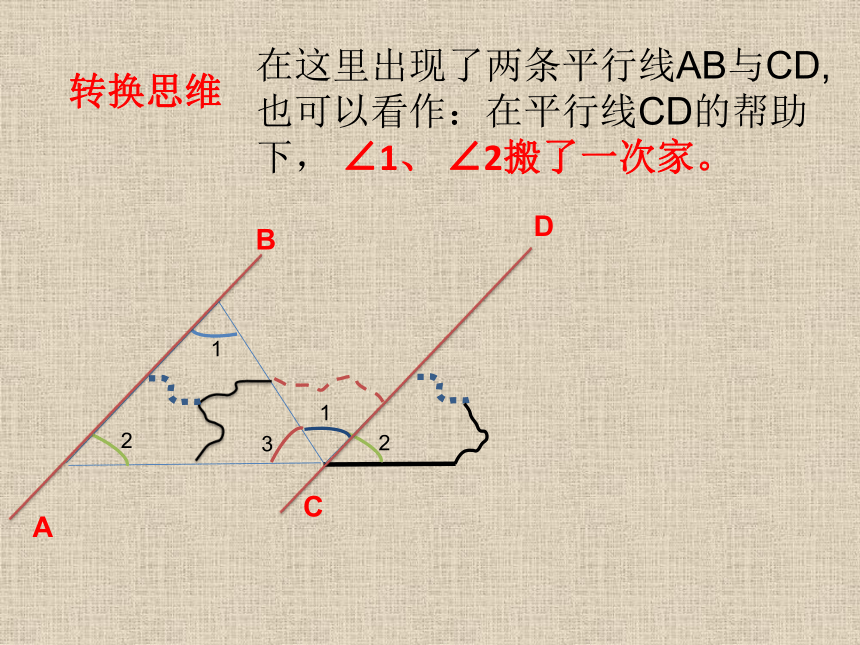
转换思维
A
B
C
D
在这里出现了两条平行线AB与CD,也可以看作:在平行线CD的帮助下, ∠1、 ∠2搬了一次家。
1
2
3
A
B
E
D
4
5
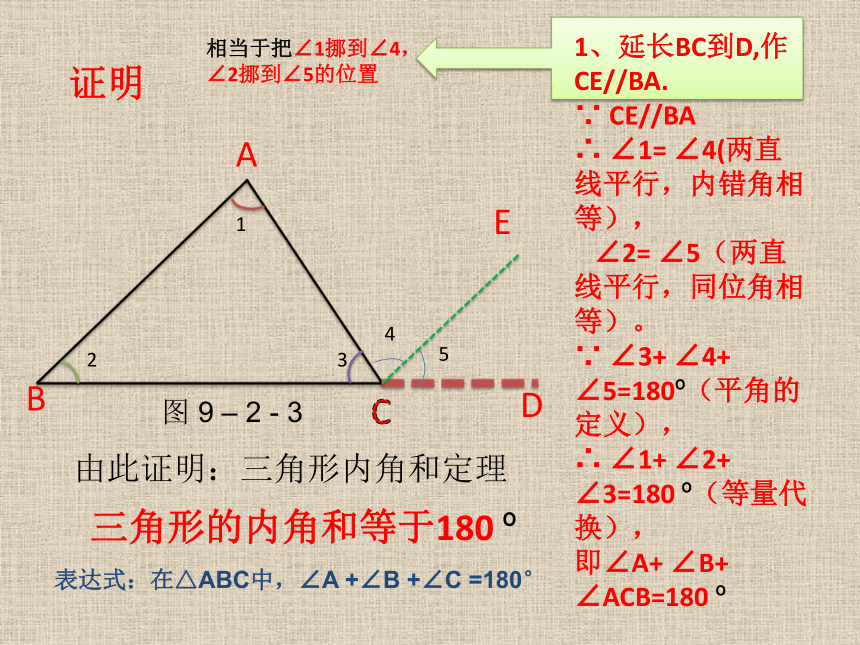
1、延长BC到D,作CE//BA.
∵ CE//BA
∴ ∠1= ∠4(两直线平行,内错角相等),
∠2= ∠5(两直线平行,同位角相等)。
∵ ∠3+ ∠4+ ∠5=180 (平角的定义),
∴ ∠1+ ∠2+ ∠3=180 (等量代换),
即∠A+ ∠B+ ∠ACB=180
由此证明:三角形内角和定理
三角形的内角和等于180
图 9 – 2 - 3
证明
相当于把∠1挪到∠4,∠2挪到∠5的位置
表达式:在△ABC中,∠A +∠B +∠C =180°
A
B
C
能不能通过三角形一个顶点作对边平行辅助线,来证明三角形内角和定理吗?
F
E
尝试拓展
在这里,为了证明的需要,在原来的图形上自己加上的线叫做辅助线。在平面几何里,辅助线通常画成虚线。注意要说明所加辅助线的位置、名称和性质。
思路总结:
为了证明三角形三个内角的和为180°,通常应用转化思想。转化为:
平角或两直线平行,同旁内角互补
C
A
B
图 9 – 2 - 5
例1 如图 9 – 2 – 5,在△ABC中,∠A=30 , ∠B=65 ,求∠C的度数。
解: ∵∠A+∠B+ ∠C=180 (三角形内角和定理),
∴∠C=180 -( ∠A+∠B ).
∵ ∠A=30 , ∠B=65 (已知).
∴∠C=180 - ( 30 +65 )=85 .
思路点拨:
应用三角形内角和等于180 ,可以从已知角求出未知角。
用180 减去两个已知角,来求未知角。
尝试练习
(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= .
(2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。
(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。
1020
400
1200
小组抢答一
在△ABC中,
1. ∠B=90 , ∠C=25 ,求∠A的度数。
2. ∠B=62 24, ∠C=28 52,求∠A的度数。
3. ∠C=42 , ∠A=∠B,求∠A的度数。
4. ∠C=36 , ∠A与∠B的比是1 ∶ 2,求∠A,∠B的度数。
小组抢答二
65
88 44
69
96
48
如图,在△ABC中,已知∠ABC=38 °, ∠ACB=62 °,AD平分∠BAC,求∠ADB的度数。
解:在△ABC中, ∠B+ ∠C+ ∠BAC=180 °
∵ ∠B=38 °, ∠C= 62 °
∴ ∠BAC=180 °— ∠B —∠C
= 180 ° — 38 °— 62 °
= 80 °
∵AD平分∠BAC,
∴ ∠BAD= ∠CAD=1/2
∠BAC=40°
在△ADB中,∠B + ∠BAD+ ∠ADB=180°
∵ ∠B=38 ° ∠BAD =40 °
∴ ∠ADB=102 °
D
已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为
20°,60°,100°。
由三角形内角和为180°得
内角和定理与比例知识、方程思想的结合。
二次尝试
求出下列图中x的值:
x
x
x
x =600
比比谁最快
x
x
x =450
2 x
x
┐
x =300
总结
1、三角形内角和定理的内容是什么?
3、三角形内角和定理的应用方向是什么?
4、三角形内角和定理与判断图形形状、方程思想、比例、一般图形转换到特殊图形的结合。
2、三角形内角和定理的证明思路是什么?
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
作业
课本P105页习题:
A组1(3)、4题
B组1题
选做题
∟
∟
A
B
C
D
在⊿ ABC中,可不可以通过做垂线,找到三角形内角和定理的证明的思路?
三角形内角和定理
1、了解并掌握三角形内角和定理的内容。
2、明确通过作辅助线来解决几何问题的思路。
4、学习并掌握从猜想到验证的几何研究方法。
3、学会简单利用三角形内角和定理计算三角形的内角度数。
学习目标
重点
1、能从多角度用多种方法证明三角形的内角和定理。
2、会在求证中添加合适的辅助线。
难点
三角形内角和定理的运用。
证明命题的一般步骤:
1、理解题意,分清命题的条件(已知),结论(求证)。
2、根据题意,画出图形。
3、结合图形,用符号语言写出已知和求证。
4、分析题意,探索证明思路。
5、依据思路,用数学符号和数学语言条理清晰地写出证明过程。
6、检查表达过程是否正确完善。
复习
A
B
C
演示
1
2
3
三角形的三个内角和是多少
方法一: 将各角沿着一边所在的直线折叠
知识链接
当我们把三角形按照图中虚线部分对折后,可以看出: ∠1、 ∠2、 ∠3的数量关系
∠1+ ∠2+ ∠3=180
A
B
C
A
B
验证
方法二:
在小学,我们通过剪拼发现了三角形的三个内角和等于180
1
2
3
除了折纸、测量、剪拼以外,我们还有没有其他方法得到三角形的内角和呢?
A
B
C
思路点拨:
如何运用“平行线”,将角挪动位置,求出三角形的内角和呢?
思考
1
2
3
1
2
转换思维
A
B
C
D
在这里出现了两条平行线AB与CD,也可以看作:在平行线CD的帮助下, ∠1、 ∠2搬了一次家。
1
2
3
A
B
E
D
4
5
1、延长BC到D,作CE//BA.
∵ CE//BA
∴ ∠1= ∠4(两直线平行,内错角相等),
∠2= ∠5(两直线平行,同位角相等)。
∵ ∠3+ ∠4+ ∠5=180 (平角的定义),
∴ ∠1+ ∠2+ ∠3=180 (等量代换),
即∠A+ ∠B+ ∠ACB=180
由此证明:三角形内角和定理
三角形的内角和等于180
图 9 – 2 - 3
证明
相当于把∠1挪到∠4,∠2挪到∠5的位置
表达式:在△ABC中,∠A +∠B +∠C =180°
A
B
C
能不能通过三角形一个顶点作对边平行辅助线,来证明三角形内角和定理吗?
F
E
尝试拓展
在这里,为了证明的需要,在原来的图形上自己加上的线叫做辅助线。在平面几何里,辅助线通常画成虚线。注意要说明所加辅助线的位置、名称和性质。
思路总结:
为了证明三角形三个内角的和为180°,通常应用转化思想。转化为:
平角或两直线平行,同旁内角互补
C
A
B
图 9 – 2 - 5
例1 如图 9 – 2 – 5,在△ABC中,∠A=30 , ∠B=65 ,求∠C的度数。
解: ∵∠A+∠B+ ∠C=180 (三角形内角和定理),
∴∠C=180 -( ∠A+∠B ).
∵ ∠A=30 , ∠B=65 (已知).
∴∠C=180 - ( 30 +65 )=85 .
思路点拨:
应用三角形内角和等于180 ,可以从已知角求出未知角。
用180 减去两个已知角,来求未知角。
尝试练习
(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= .
(2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。
(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。
1020
400
1200
小组抢答一
在△ABC中,
1. ∠B=90 , ∠C=25 ,求∠A的度数。
2. ∠B=62 24, ∠C=28 52,求∠A的度数。
3. ∠C=42 , ∠A=∠B,求∠A的度数。
4. ∠C=36 , ∠A与∠B的比是1 ∶ 2,求∠A,∠B的度数。
小组抢答二
65
88 44
69
96
48
如图,在△ABC中,已知∠ABC=38 °, ∠ACB=62 °,AD平分∠BAC,求∠ADB的度数。
解:在△ABC中, ∠B+ ∠C+ ∠BAC=180 °
∵ ∠B=38 °, ∠C= 62 °
∴ ∠BAC=180 °— ∠B —∠C
= 180 ° — 38 °— 62 °
= 80 °
∵AD平分∠BAC,
∴ ∠BAD= ∠CAD=1/2
∠BAC=40°
在△ADB中,∠B + ∠BAD+ ∠ADB=180°
∵ ∠B=38 ° ∠BAD =40 °
∴ ∠ADB=102 °
D
已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为
20°,60°,100°。
由三角形内角和为180°得
内角和定理与比例知识、方程思想的结合。
二次尝试
求出下列图中x的值:
x
x
x
x =600
比比谁最快
x
x
x =450
2 x
x
┐
x =300
总结
1、三角形内角和定理的内容是什么?
3、三角形内角和定理的应用方向是什么?
4、三角形内角和定理与判断图形形状、方程思想、比例、一般图形转换到特殊图形的结合。
2、三角形内角和定理的证明思路是什么?
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
作业
课本P105页习题:
A组1(3)、4题
B组1题
选做题
∟
∟
A
B
C
D
在⊿ ABC中,可不可以通过做垂线,找到三角形内角和定理的证明的思路?
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
