冀教版数学七年级下册 11.1 因式分解-回顾与反思课件(共31张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 11.1 因式分解-回顾与反思课件(共31张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
目标一
目标二
目标三
目标四
进一步理解因式分解的意义及方法。
熟练运用不同方法进行因式分解解决问题。
通过对本章学习过程的总结与梳理
进一步认识本章知识间的内在联系。
提炼概括本章蕴含的数学思想方法
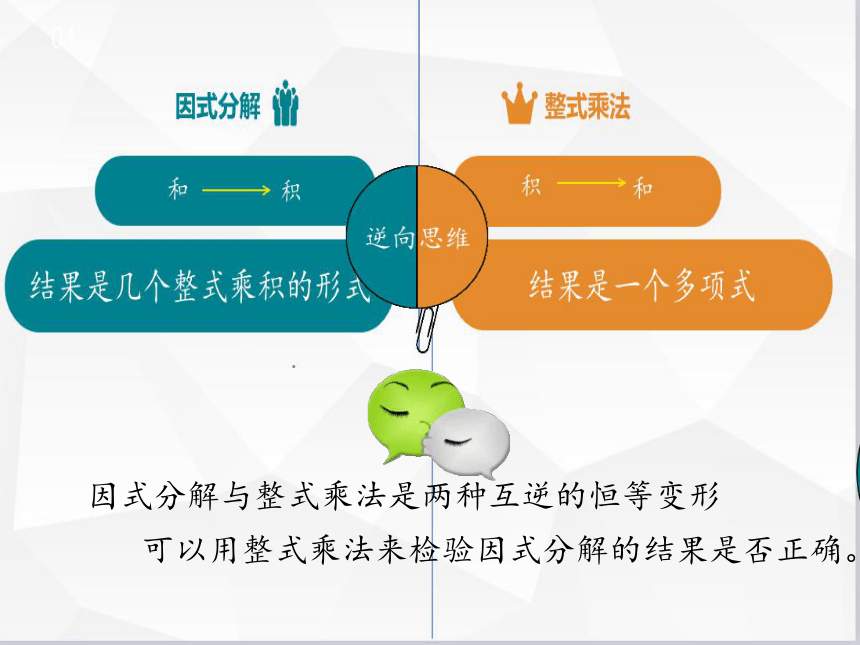
一般地,把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解,也叫做将多项式分解因式。
一个多项式
几个整式乘积
和
积
1、3x -6x -3x=3x(x -2x-1)
2、x +2x-3=x(x+2)-3
3、m -m -m=m(m -m-1)
4、(a+b)(a-b)=a -b
因式分解与整式乘法是两种互逆的恒等变形
可以用整式乘法来检验因式分解的结果是否正确。
若关于x的多项式3x +mx+n分解因式的结果
(3x+2)(x-1),求m,n的值。
公式中的a,b
即可表示单项式,又可以表示多项式
运用公式时,
要对应好公式中的a,b,再按公式分解因式
A.因式分解的意义
B.因式分解的方法
C.因式分解的综合
D.因式分解与图形
E.因式分解方法拓展
因式分解的应用
D.a +4a-21=(a+2) -25
下列式子从左到右的变形,是因式分解的是( )
B.a +4a-21=(a-3)(a+7)
C.(a-3)(a+7)=a +4a-21
A.a +4a-21=a(a+4)-21
把分解因式正确的呼喊过来吧!
-x +4x=-x(x+4)
x +xy+x=x(x+y)
-x +2xy-y =-(x-y)
x -4x+4=(x-2)
x +y =(x+y)
若Ia+b-6I+(ab-4) =0,
求-a b-2a b -ab 的值。
已知x +y -4x+6y+13=0,
求x和y的值。
若(x +y )(x +y -2)+1=0,
求x +y 的值。
试一试:多项式
(a-b) +4ab能进行因式分解吗?请你试着分解(x+y) -4(x+y-1)
将一个多项式分组后,
再提公因式或运用公式继续分解的方法是分组分解法。
am+an+bm+bn
=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
a -2ab+ac-bc+b
例子
分组分解法
如果9x +kxy+4y 是一个完全平方式,
那么k的值为?
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),
余下的部分剪拼成一个矩形。通过计算阴影部分的面积,验证了一个等式,
这个等式是( )。
A.a -b =(a+b)(a-b)
B.(a+b) =a +2ab+b
C.(a-b) =a -2ab+b
D.a -ab=a(a-b)
1、已知a,b,c分别是△ABC三边的长,且满足a +2b +c -2b(a+c)=0.试判断三角形的形状。
2、试说明x,y取何值,x +y -4x+6y+15的值总大于0.利用因式分解计算:1-2 +3 -4 +5 -6 +…+99 -100 +101 。
思考题
目标一
目标二
目标三
目标四
进一步理解因式分解的意义及方法。
熟练运用不同方法进行因式分解解决问题。
通过对本章学习过程的总结与梳理
进一步认识本章知识间的内在联系。
提炼概括本章蕴含的数学思想方法
一般地,把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解,也叫做将多项式分解因式。
一个多项式
几个整式乘积
和
积
1、3x -6x -3x=3x(x -2x-1)
2、x +2x-3=x(x+2)-3
3、m -m -m=m(m -m-1)
4、(a+b)(a-b)=a -b
因式分解与整式乘法是两种互逆的恒等变形
可以用整式乘法来检验因式分解的结果是否正确。
若关于x的多项式3x +mx+n分解因式的结果
(3x+2)(x-1),求m,n的值。
公式中的a,b
即可表示单项式,又可以表示多项式
运用公式时,
要对应好公式中的a,b,再按公式分解因式
A.因式分解的意义
B.因式分解的方法
C.因式分解的综合
D.因式分解与图形
E.因式分解方法拓展
因式分解的应用
D.a +4a-21=(a+2) -25
下列式子从左到右的变形,是因式分解的是( )
B.a +4a-21=(a-3)(a+7)
C.(a-3)(a+7)=a +4a-21
A.a +4a-21=a(a+4)-21
把分解因式正确的呼喊过来吧!
-x +4x=-x(x+4)
x +xy+x=x(x+y)
-x +2xy-y =-(x-y)
x -4x+4=(x-2)
x +y =(x+y)
若Ia+b-6I+(ab-4) =0,
求-a b-2a b -ab 的值。
已知x +y -4x+6y+13=0,
求x和y的值。
若(x +y )(x +y -2)+1=0,
求x +y 的值。
试一试:多项式
(a-b) +4ab能进行因式分解吗?请你试着分解(x+y) -4(x+y-1)
将一个多项式分组后,
再提公因式或运用公式继续分解的方法是分组分解法。
am+an+bm+bn
=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
a -2ab+ac-bc+b
例子
分组分解法
如果9x +kxy+4y 是一个完全平方式,
那么k的值为?
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),
余下的部分剪拼成一个矩形。通过计算阴影部分的面积,验证了一个等式,
这个等式是( )。
A.a -b =(a+b)(a-b)
B.(a+b) =a +2ab+b
C.(a-b) =a -2ab+b
D.a -ab=a(a-b)
1、已知a,b,c分别是△ABC三边的长,且满足a +2b +c -2b(a+c)=0.试判断三角形的形状。
2、试说明x,y取何值,x +y -4x+6y+15的值总大于0.利用因式分解计算:1-2 +3 -4 +5 -6 +…+99 -100 +101 。
思考题
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
