沪科版八年级下册 19.3 矩形 菱形 正方形课件(共32张PPT)
文档属性
| 名称 | 沪科版八年级下册 19.3 矩形 菱形 正方形课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 647.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 07:11:21 | ||
图片预览




文档简介
(共32张PPT)
矩形
矩形、菱形、正方形
有一个角是直角的平行四边形是矩形
矩形的定义:
一般性质:
具备平行四边形所有的性质
对边平行
对边相等,
对角相等,
对角线互相平分
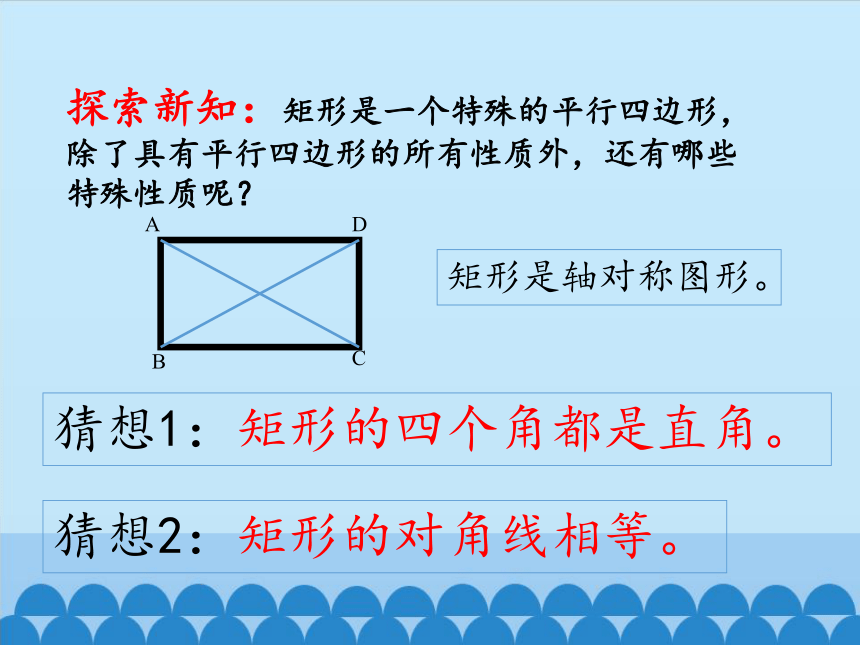
探索新知:矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角。
猜想2:矩形的对角线相等。
矩形是轴对称图形。
A
B
C
D
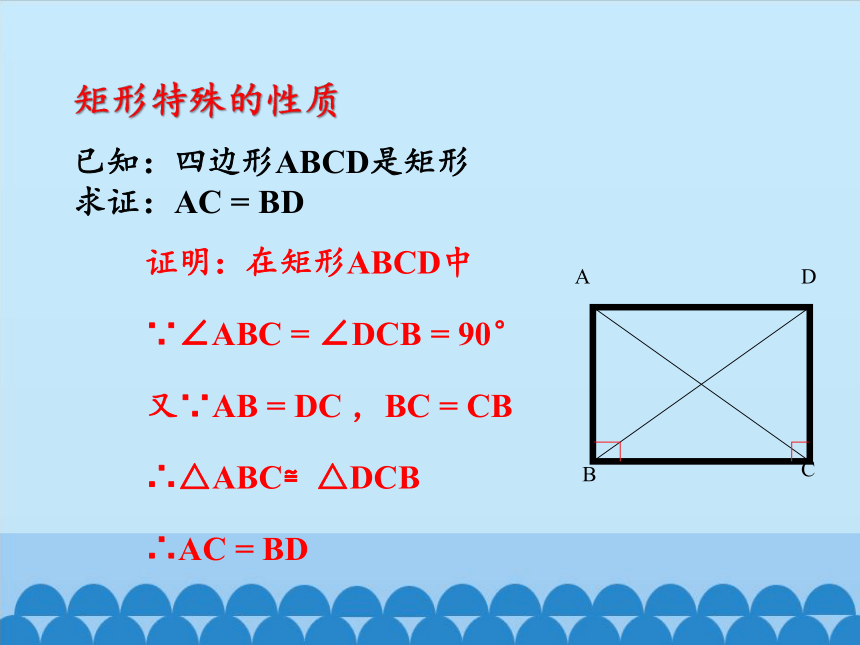
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ,BC = CB
∴△ABC≌△DCB
∴AC = BD
矩形特殊的性质
矩形特殊的性质
矩形的四个角都是直角。
矩形的两条对角线相等。
从角上看:
从对角线上看:
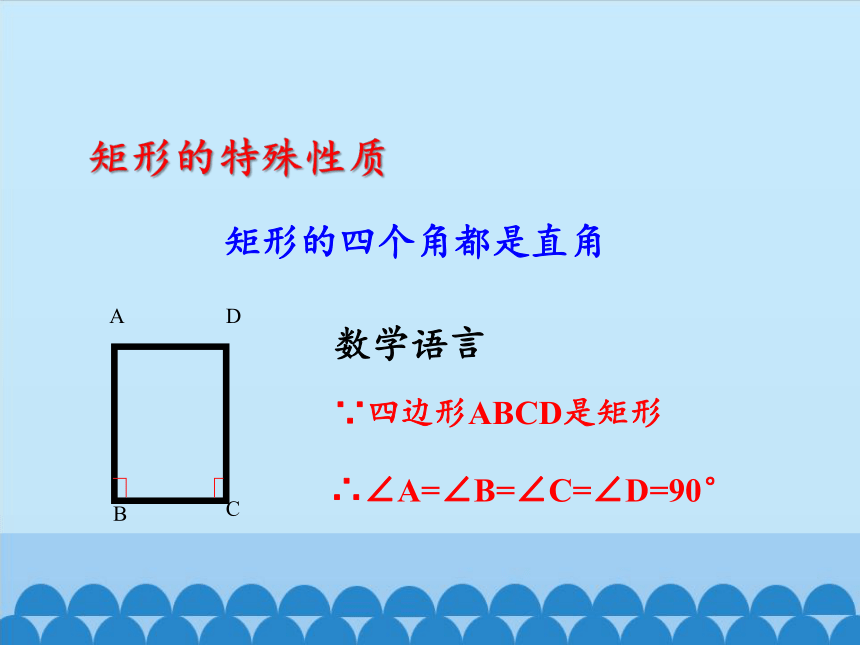
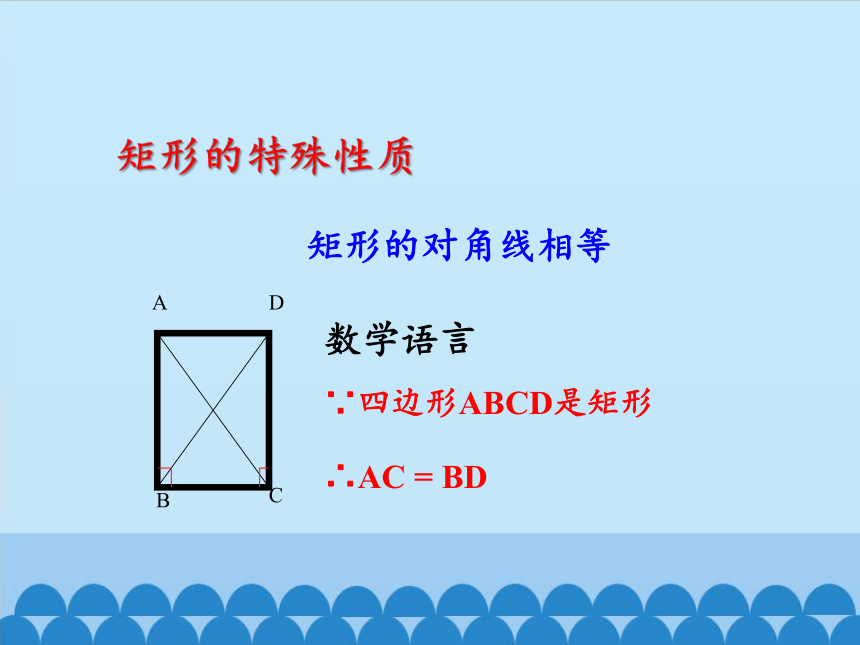
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
矩形的特殊性质
矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
O
A
B
C
D
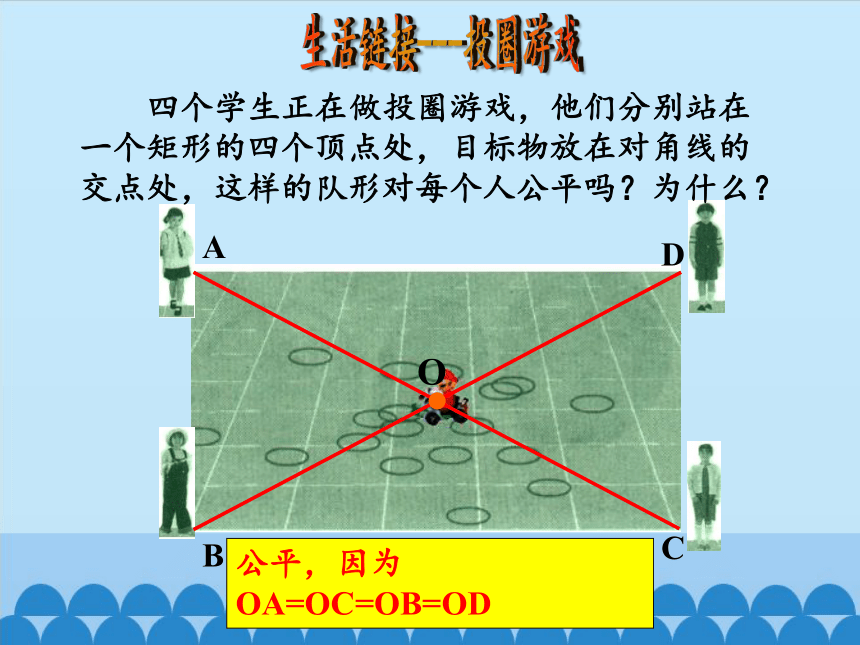
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
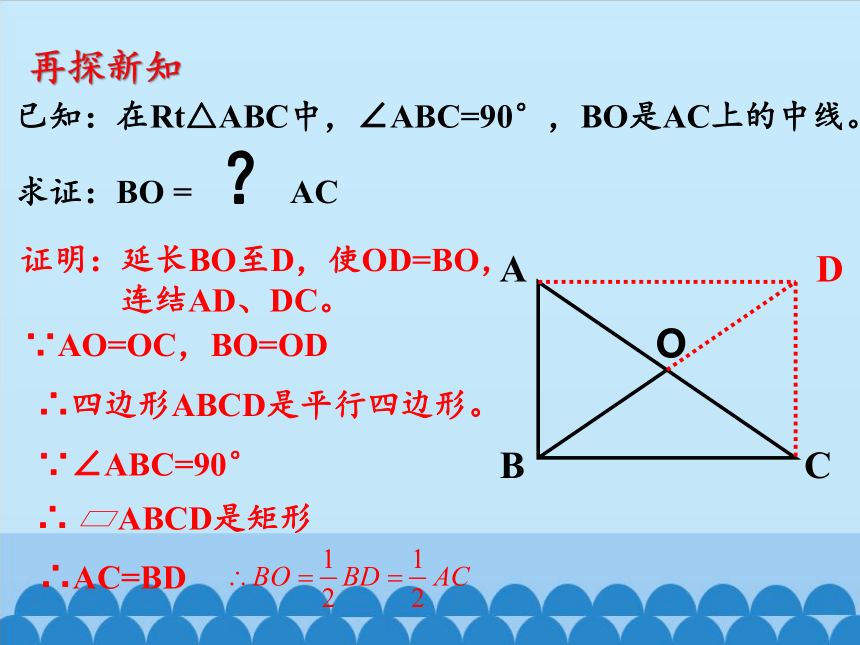
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线。
求证:BO = ?AC
O
C
B
A
D
证明:延长BO至D,使OD=BO,
连结AD、DC。
∵AO=OC,BO=OD
∴四边形ABCD是平行四边形。
∵∠ABC=90°
∴ ABCD是矩形
∴AC=BD
再探新知
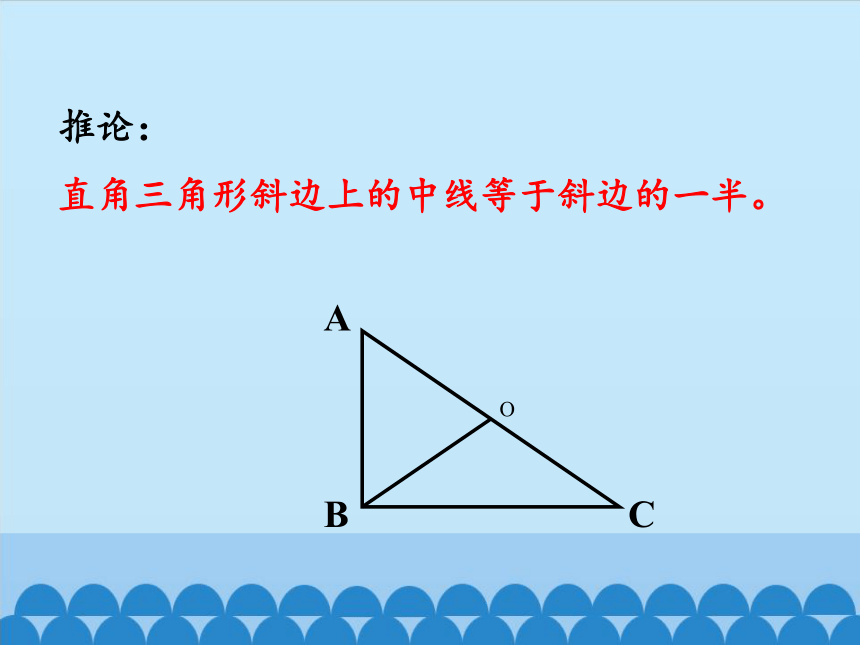
推论:
直角三角形斜边上的中线等于斜边的一半。
C
B
A
O
例1:如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=4㎝,求矩形对角线的长?
解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=120°
∴ △AOD是等边三角形
∴ OA=AD=4(㎝)
∴ 矩形的对角线长
AC=BD=2OA=8(㎝)
B
C
D
A
O
方法小结:
如果矩形两对角 线的夹角是60°或120°, 则其中必有等边三角形。
如图,在矩形ABCD中,找出相等的线段与相等的角。
A
D
C
B
O
想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三解形,有几对全等的等腰三角形?
小试牛刀
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
课堂训练
2.四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=___ ㎝,OB=___ ㎝
(2)若已知AC=10㎝,BC=6㎝,则矩形
周长=____ cm,矩形的面积=_______ ㎝2
(3)若已知 ∠DOC=120°,AC=8㎝,则
AD= _____cm, AB= _____cm
O
D
C
B
A
5
10
4
48
28
四边形
平行
四边形
两组对
边平行
一个角
是直角
∟
矩形
平行四边形□
矩形
四边形
知识回顾
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
情境:
你现在有办法帮他吗?
分析矩形的定义:
有一个角是直角的平行四边形是矩形。
∵ □ ABCD
∠A=90°
∴ □ ABCD是矩形
①
②
由定义判定:
A
B
C
D
由定义入手:
矩形的四个角都是直角
条件
结论
四个角是直角的四边形是矩形
条件
结论
①任意画一个符合条件的图形,通过观察、测量猜想其形状;
探究1
性质:
逆命题:
操作感知:
李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形。猜想她判断的依据?
有三个角是直角的四边形是矩形
你能证明上述结论吗?
A
B
D
C
她这样做:
猜想:
有三个角是直角的四边形是矩形
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
符号表达式:
矩形的判定方法(2)
如图,BD,BE分别是∠ABC与它的邻补角∠CBP的平分线,CE⊥BE,CD⊥BD,E,D为垂足,猜一猜:四边形BECD的形状。
A
B
C
D
E
P
找三个角是直角
∵ BD,BE分别是∠ABC与它的邻补角∠CBP的平分线
∴∠DBE=90°
又∵ CE⊥BE,CD⊥BD
∴四边形BECD是矩形
∴∠D=∠E=90°
试一试:
说说你的想法……
证明:
矩形的对角线相等
条件
结论
对角线相等的平行四边形是矩形
②任意画一个符合条件的图形,通过观察、测量猜想其形状确定真命题;
对角线相等的四边形是矩形
探究2
性质:
逆命题:
操作感知:
∵ 在□ ABCD中,AB=DC,
BC=CB, 且AC=DB
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
∴ ∠ABC=∠DCB
命题:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD
求证: □ ABCD是矩形
A
B
C
D
证明:
A
B
C
D
O
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形
符号表达式:
矩形的判定方法(3)
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形。
(对角线平分且相等的四边形是矩形)
有三个角是直角的四边形是矩形。
方法1:
方法2:
方法3:
测量……?
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
方案:
方案:
方案:
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
√
×
×
×
√
√
×
×
√
√
2.如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。
A
B
C
D
M
本课小结
矩形的四个角都是直角。
※ 矩形的性质定理1
矩形的对角线相等。
※ 矩形的性质定理2
※ 推 论
直角三角形斜边上的中线等于斜边的一半。
矩形定义:
有一个角是直角的平行四边形叫做矩形。
作业
课本
课本习题
谢 谢
矩形
矩形、菱形、正方形
有一个角是直角的平行四边形是矩形
矩形的定义:
一般性质:
具备平行四边形所有的性质
对边平行
对边相等,
对角相等,
对角线互相平分
探索新知:矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角。
猜想2:矩形的对角线相等。
矩形是轴对称图形。
A
B
C
D
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ,BC = CB
∴△ABC≌△DCB
∴AC = BD
矩形特殊的性质
矩形特殊的性质
矩形的四个角都是直角。
矩形的两条对角线相等。
从角上看:
从对角线上看:
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
矩形的特殊性质
矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线。
求证:BO = ?AC
O
C
B
A
D
证明:延长BO至D,使OD=BO,
连结AD、DC。
∵AO=OC,BO=OD
∴四边形ABCD是平行四边形。
∵∠ABC=90°
∴ ABCD是矩形
∴AC=BD
再探新知
推论:
直角三角形斜边上的中线等于斜边的一半。
C
B
A
O
例1:如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=4㎝,求矩形对角线的长?
解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=120°
∴ △AOD是等边三角形
∴ OA=AD=4(㎝)
∴ 矩形的对角线长
AC=BD=2OA=8(㎝)
B
C
D
A
O
方法小结:
如果矩形两对角 线的夹角是60°或120°, 则其中必有等边三角形。
如图,在矩形ABCD中,找出相等的线段与相等的角。
A
D
C
B
O
想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三解形,有几对全等的等腰三角形?
小试牛刀
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
课堂训练
2.四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=___ ㎝,OB=___ ㎝
(2)若已知AC=10㎝,BC=6㎝,则矩形
周长=____ cm,矩形的面积=_______ ㎝2
(3)若已知 ∠DOC=120°,AC=8㎝,则
AD= _____cm, AB= _____cm
O
D
C
B
A
5
10
4
48
28
四边形
平行
四边形
两组对
边平行
一个角
是直角
∟
矩形
平行四边形□
矩形
四边形
知识回顾
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
情境:
你现在有办法帮他吗?
分析矩形的定义:
有一个角是直角的平行四边形是矩形。
∵ □ ABCD
∠A=90°
∴ □ ABCD是矩形
①
②
由定义判定:
A
B
C
D
由定义入手:
矩形的四个角都是直角
条件
结论
四个角是直角的四边形是矩形
条件
结论
①任意画一个符合条件的图形,通过观察、测量猜想其形状;
探究1
性质:
逆命题:
操作感知:
李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形。猜想她判断的依据?
有三个角是直角的四边形是矩形
你能证明上述结论吗?
A
B
D
C
她这样做:
猜想:
有三个角是直角的四边形是矩形
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
符号表达式:
矩形的判定方法(2)
如图,BD,BE分别是∠ABC与它的邻补角∠CBP的平分线,CE⊥BE,CD⊥BD,E,D为垂足,猜一猜:四边形BECD的形状。
A
B
C
D
E
P
找三个角是直角
∵ BD,BE分别是∠ABC与它的邻补角∠CBP的平分线
∴∠DBE=90°
又∵ CE⊥BE,CD⊥BD
∴四边形BECD是矩形
∴∠D=∠E=90°
试一试:
说说你的想法……
证明:
矩形的对角线相等
条件
结论
对角线相等的平行四边形是矩形
②任意画一个符合条件的图形,通过观察、测量猜想其形状确定真命题;
对角线相等的四边形是矩形
探究2
性质:
逆命题:
操作感知:
∵ 在□ ABCD中,AB=DC,
BC=CB, 且AC=DB
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
∴ ∠ABC=∠DCB
命题:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD
求证: □ ABCD是矩形
A
B
C
D
证明:
A
B
C
D
O
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形
符号表达式:
矩形的判定方法(3)
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形。
(对角线平分且相等的四边形是矩形)
有三个角是直角的四边形是矩形。
方法1:
方法2:
方法3:
测量……?
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
方案:
方案:
方案:
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
√
×
×
×
√
√
×
×
√
√
2.如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。
A
B
C
D
M
本课小结
矩形的四个角都是直角。
※ 矩形的性质定理1
矩形的对角线相等。
※ 矩形的性质定理2
※ 推 论
直角三角形斜边上的中线等于斜边的一半。
矩形定义:
有一个角是直角的平行四边形叫做矩形。
作业
课本
课本习题
谢 谢
