高中数学 1.3.1函数的单调性与导数 课件
文档属性
| 名称 | 高中数学 1.3.1函数的单调性与导数 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 241.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-06 00:00:00 | ||
图片预览



文档简介
课件11张PPT。函数的单调性与导数(5)对数函数的导数:(4)指数函数的导数: (3)三角函数 : (1)常函数:(C)/ ? 0, (c为常数); (2)幂函数 : (xn)/ ? nxn?1
回顾:1.基本初等函数的导数公式 2.导数的运算法则(1)函数的和或差的导数
(u±v)/=u/±v/.
(3)函数的商的导数
( ) / = (v≠0)。
(2)函数的积的导数
(uv)/=u/v+v/u.
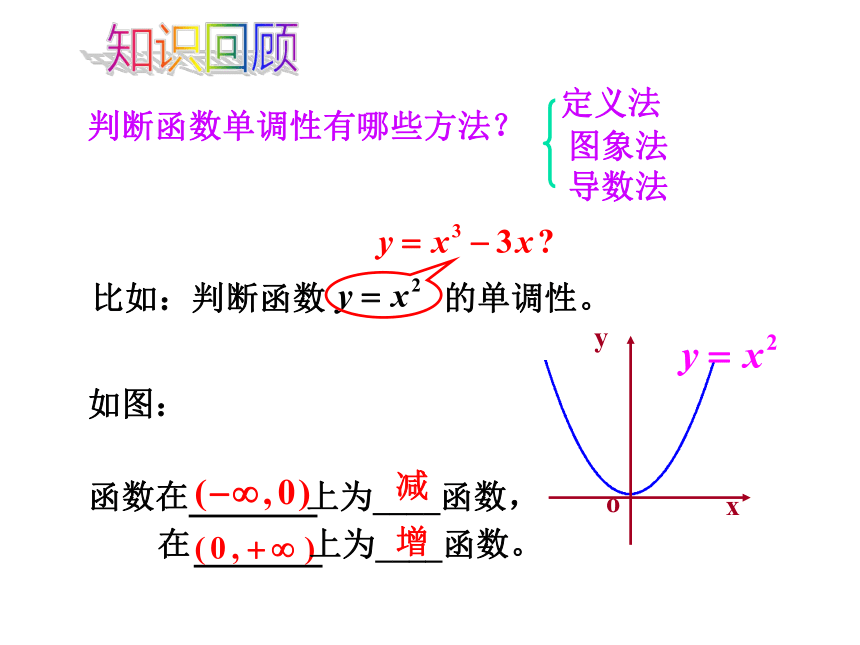
知识回顾判断函数单调性有哪些方法?比如:判断函数 的单调性。图象法
导数法减增如图:动态
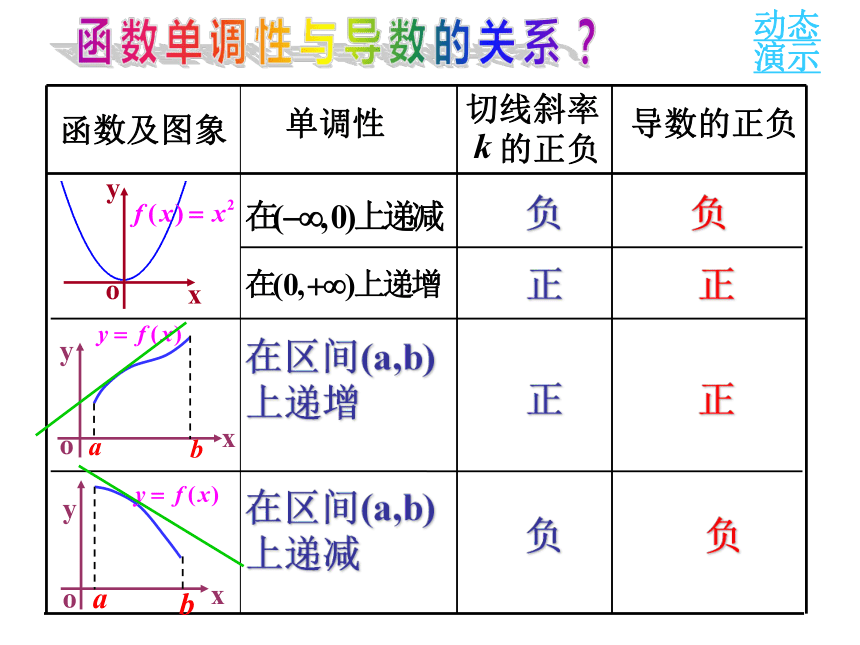
演示单调性导数的正负函数及图象切线斜率
的正负函数单调性与导数的关系?负正负正在区间(a,b)上递增在区间(a,b)上递减正正负负f '(x)>0f '(x)<0由上我们可得以下的结论:如果在某个区间内恒有 ,则 为常数. 定义:一般地,设函数y=f (x)在某个区间(a,b)内有导数,如果在 这个区间内 >0,那么函数y=f (x) 在为这个区间内 的增函数;如果在这个区间内 <0,那么函数y=f (x) 在为这个区间内的减函数. 求函数 的单调区间。变1:求函数 的单调区间。理解训练:解:的单调递增区间为单调递减区间为变3:求函数 的单调区间。解:解:总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。纳注意:函数定义域①求②令③求单调区间1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?2°试总结用“导数法” 求单调区间的步骤?归高考试B尝练习: 求函数的单调区间: f (x)=x/2+sinx;已知导函数的下列信息:试画出函数 图象的大致形状。分析:解: 的大致形状如右图:2.应用导数信息确定函数大致图象(A)(B)(C)(D)C高考试尝设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
回顾:1.基本初等函数的导数公式 2.导数的运算法则(1)函数的和或差的导数
(u±v)/=u/±v/.
(3)函数的商的导数
( ) / = (v≠0)。
(2)函数的积的导数
(uv)/=u/v+v/u.
知识回顾判断函数单调性有哪些方法?比如:判断函数 的单调性。图象法
导数法减增如图:动态
演示单调性导数的正负函数及图象切线斜率
的正负函数单调性与导数的关系?负正负正在区间(a,b)上递增在区间(a,b)上递减正正负负f '(x)>0f '(x)<0由上我们可得以下的结论:如果在某个区间内恒有 ,则 为常数. 定义:一般地,设函数y=f (x)在某个区间(a,b)内有导数,如果在 这个区间内 >0,那么函数y=f (x) 在为这个区间内 的增函数;如果在这个区间内 <0,那么函数y=f (x) 在为这个区间内的减函数. 求函数 的单调区间。变1:求函数 的单调区间。理解训练:解:的单调递增区间为单调递减区间为变3:求函数 的单调区间。解:解:总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。纳注意:函数定义域①求②令③求单调区间1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?2°试总结用“导数法” 求单调区间的步骤?归高考试B尝练习: 求函数的单调区间: f (x)=x/2+sinx;已知导函数的下列信息:试画出函数 图象的大致形状。分析:解: 的大致形状如右图:2.应用导数信息确定函数大致图象(A)(B)(C)(D)C高考试尝设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
