高中数学 1.3.2《函数的极值与导数》课件
文档属性
| 名称 | 高中数学 1.3.2《函数的极值与导数》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 90.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-06 00:00:00 | ||
图片预览






文档简介
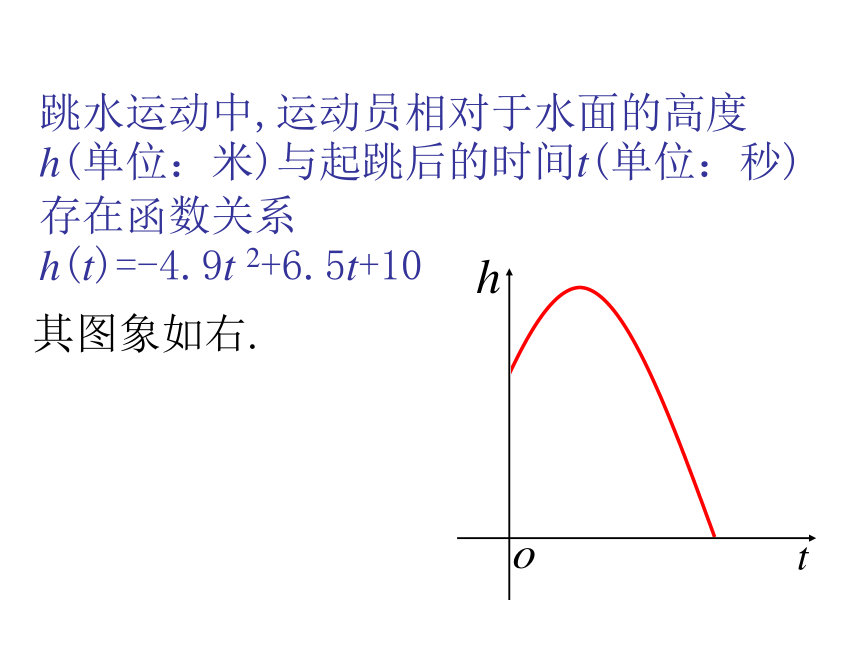
课件25张PPT。3.3.2 函数的极值与导数1.3.2 导数及其应用跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t 2+6.5t+10其图象如右.单调递增单调递减对于d点
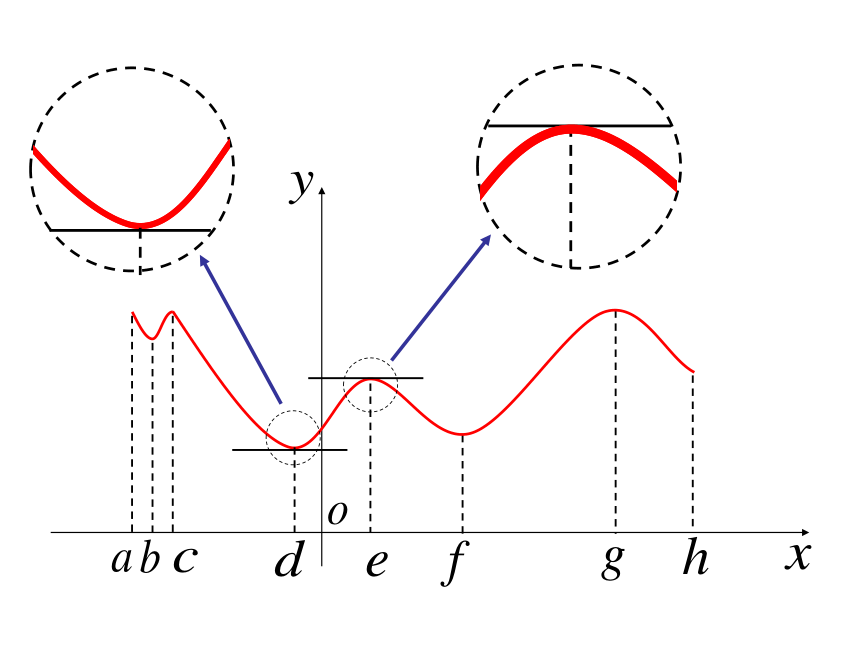
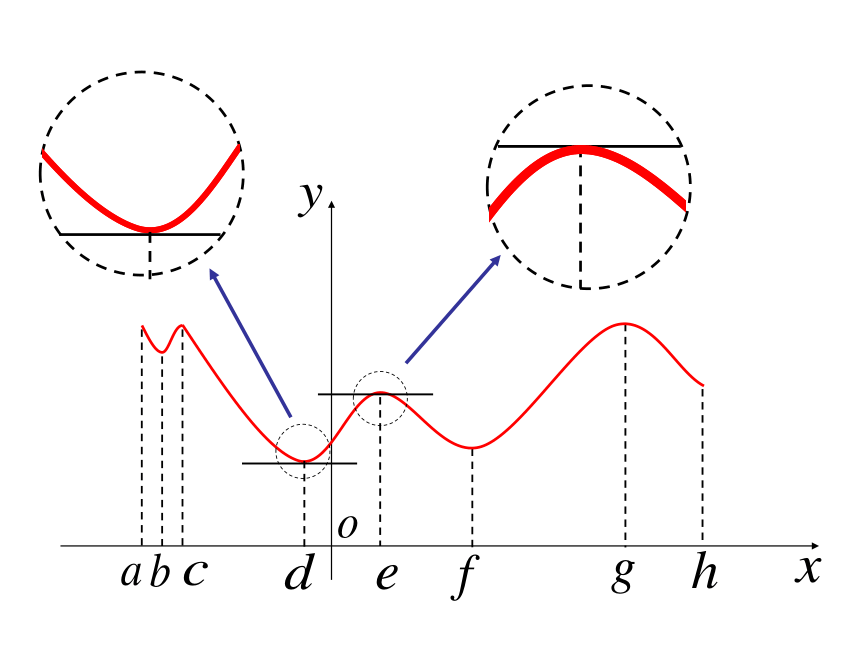
函数y=f(x)在点x=d的函数值f(d)比在其附
近其他点的函数值都小, =0 。在点x=d 附近的左侧 <0
在点x=d 附近的右侧 >0我们把点d叫做函数y=f(x)的极小值点,
f(d)叫做函数y=f(x)的极小值。在点 x=e 附近的左侧 >0
在点 x=e 附近的右侧 <0对于e点
函数y=f(x)在点x=e的函数值f(e)比在其附
近其他点的函数值都大, =0 。我们把点e叫做函数y=f(x)的极大值点,
f(e)叫做函数y=f(x)的极大值。极小值点、极大值点统称为极值点极小值、极大值统称为极值极大值一定大于极小值吗?不一定例1、求函数f(x)=x3-12x+12的极值。解: =3x2-12=3(x-2)(x+2)令 =0得x=2,或x=-2下面分两种情况讨论:(1)当 >0即x>2,或x<-2时;(2)当 <0即-2 并且极大值为f(-2)=28当x=2时,f(x)有极小值,
并且极小值为f(2)=-4图象如右练习1、求函数f(x)=6+12x-x3 =12-3x2=3(4-x2)=3(2-x)(2+x)一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.即“峰顶”即“谷底”例2、已知函数f(x)=ax3+bx2-2x在x=-2,x=1
处取得极值:
(1)求函数的解析式;
(2)求函数f(x)的单调区间。解:(1) =3ax2+2bx-2因为f(x)在x=-2,x=1处取得极值,所以 解得 =3ax2+2bx-2即f(x)=ax3+bx2-2x =x2+x-2由 >0,得x<-2或x>1,
所以f(x)的单调增区间为(-∞,-2) ∪(1,+∞)由 <0,得-2所以f(x)的单调减区间为(-2,1)导数值为0的点一定是函数的极值点吗?思考但x=0不是函数的极值点导数为零的点是
该点为极值点的必要条件,
而不是充分条件.例3:已知f(x)=ax5-bx3+c在x= 1处有极值,且极大值为
4,极小值为0.试确定a,b,c的值.解:由题意, 应有根 ,故5a=3b,于是:(1)设a>0,列表如下:由表可得 ,即 .又5a=3b,解得a=3,b=5,c=2.(2)设a<0,列表如下:由表可得 ,即 .又5a=3b,解得a=-3,b=-5,c=2.练习2:已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为
10,求a、b的值.解: =3x2+2ax+b=0有一个根x=1,故3+2a+b=0.①又f(1)=10,故1+a+b+a2=10.②由①、②解得 或当a=-3,b=3时, ,此时f(x)在x=1处无
极值,不合题意.当a=4,b=-11时,-3/111时, ,此时x=1是极
值点.从而所求的解为a=4,b=-11.小结一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.即“峰顶”即“谷底”再见
h(t)=-4.9t 2+6.5t+10其图象如右.单调递增单调递减对于d点
函数y=f(x)在点x=d的函数值f(d)比在其附
近其他点的函数值都小, =0 。在点x=d 附近的左侧 <0
在点x=d 附近的右侧 >0我们把点d叫做函数y=f(x)的极小值点,
f(d)叫做函数y=f(x)的极小值。在点 x=e 附近的左侧 >0
在点 x=e 附近的右侧 <0对于e点
函数y=f(x)在点x=e的函数值f(e)比在其附
近其他点的函数值都大, =0 。我们把点e叫做函数y=f(x)的极大值点,
f(e)叫做函数y=f(x)的极大值。极小值点、极大值点统称为极值点极小值、极大值统称为极值极大值一定大于极小值吗?不一定例1、求函数f(x)=x3-12x+12的极值。解: =3x2-12=3(x-2)(x+2)令 =0得x=2,或x=-2下面分两种情况讨论:(1)当 >0即x>2,或x<-2时;(2)当 <0即-2
并且极小值为f(2)=-4图象如右练习1、求函数f(x)=6+12x-x3 =12-3x2=3(4-x2)=3(2-x)(2+x)一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.即“峰顶”即“谷底”例2、已知函数f(x)=ax3+bx2-2x在x=-2,x=1
处取得极值:
(1)求函数的解析式;
(2)求函数f(x)的单调区间。解:(1) =3ax2+2bx-2因为f(x)在x=-2,x=1处取得极值,所以 解得 =3ax2+2bx-2即f(x)=ax3+bx2-2x =x2+x-2由 >0,得x<-2或x>1,
所以f(x)的单调增区间为(-∞,-2) ∪(1,+∞)由 <0,得-2
该点为极值点的必要条件,
而不是充分条件.例3:已知f(x)=ax5-bx3+c在x= 1处有极值,且极大值为
4,极小值为0.试确定a,b,c的值.解:由题意, 应有根 ,故5a=3b,于是:(1)设a>0,列表如下:由表可得 ,即 .又5a=3b,解得a=3,b=5,c=2.(2)设a<0,列表如下:由表可得 ,即 .又5a=3b,解得a=-3,b=-5,c=2.练习2:已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为
10,求a、b的值.解: =3x2+2ax+b=0有一个根x=1,故3+2a+b=0.①又f(1)=10,故1+a+b+a2=10.②由①、②解得 或当a=-3,b=3时, ,此时f(x)在x=1处无
极值,不合题意.当a=4,b=-11时,-3/11
值点.从而所求的解为a=4,b=-11.小结一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.即“峰顶”即“谷底”再见
