二元一次方程组复习 学案
图片预览

文档简介
369模式七年级数学导学案
课题:第八章二元一次方程组复习(1-2)
主备:代令 集体备课:张、龚 总课时:总第49.50课时
一、学习目标:
1. 知道第八章二元一次方程组知识结构图.
2.通过基本训练,巩固第八章所学的基本内容.
3.通过典型例题和综合运用,加深理解第八章所学的基本内容,发展能力.
二、学习重点和难点:
1.重点:知识结构图和基本训练.
2.难点:典型例题和综合运用.
三、归纳总结,完善认知:(阅读P117页及全章内容回答下列问题)
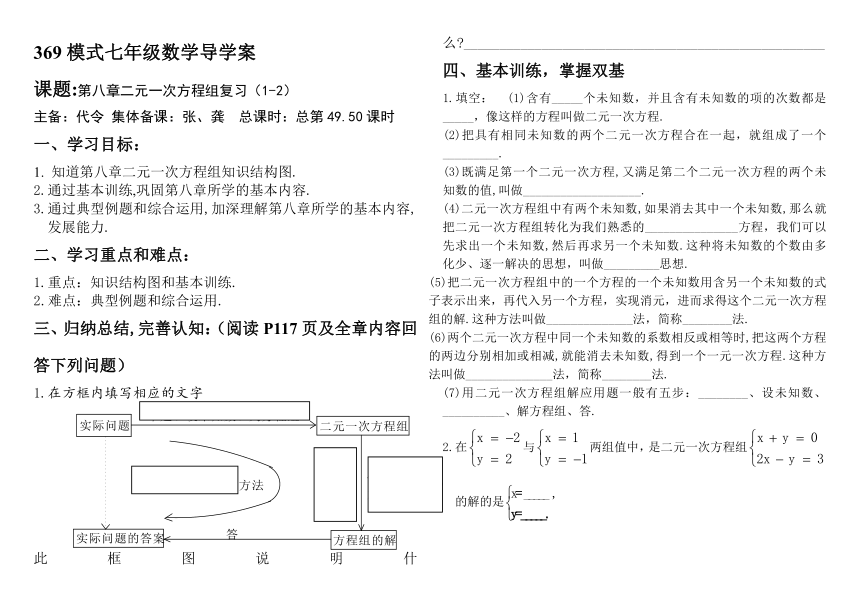
1.在方框内填写相应的文字
此框图说明什么 ___________________________________________________
四、基本训练,掌握双基
1.填空: (1)含有_____个未知数,并且含有未知数的项的次数都是_____,像这样的方程叫做二元一次方程.
(2)把具有相同未知数的两个二元一次方程合在一起,就组成了一个_________.
(3)既满足第一个二元一次方程,又满足第二个二元一次方程的两个未知数的值,叫做___________________.
(4)二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为我们熟悉的_______________方程,我们可以先求出一个未知数,然后再求另一个未知数.这种将未知数的个数由多化少、逐一解决的思想,叫做_________思想.
(5)把二元一次方程组中的一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做______________法,简称________法.
(6)两个二元一次方程中同一个未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去未知数,得到一个一元一次方程.这种方法叫做______________法,简称________法.
(7)用二元一次方程组解应用题一般有五步:________、设未知数、__________、解方程组、答.
2.在与两组值中,是二元一次方程组的解的是
3.完成下面的解题过程: 4.用代入法解方程组 用代入法解方程组
解:由①,得x=____________.③
把③代入②,得_______________.
解这个方程,得y=_____.
把y=_____代入③,得x=_____.
所以这个方程组的解是
5.完成下面的解题过程: 6.用加减法解方程组 用加减法解方程组
解: 解:①×3,得_________________.③
②+③,得________________.
x=______.
把x=______代入____,得__________,
y=______.
所以这个方程组的解是
7.解方程组
五、综合运用,发展能力
9. 2台大收割机和5台小收割机都工作2小时共收割青稞3.6公顷,3台大收割机和2台小收割机都工作5小时共收割青稞8公顷.1台大收割机和1台小收割机每小时各收割青稞多少公顷?
10.填空:已知二元一次方程组的解是,则m=_____,n=_____.
11.填空:某班学生共40人,男生比女生少3人,问男女生各多少人?设男生x人,女生y人.根据题意列方程组,得
12.填空:2本练习本及3支铅笔的价格为3.2元,4本练习本和5支铅笔的价格为5.8元.问一本练习本和一支铅笔的价格各为多少?设一本练习本的价格为x元,一支铅笔的价格为y元.根据题意列方程组,得
13.填空:某班上数学课的时候,准备分组讨论.如果每组7人,则余下3人;如果每组8人,则又不足5人.问全班有多少人?要分几组?设全班有x人,要分y组.根据题意列方程组,得
14.填空:某家存入银行甲、乙两种不同性质的存款20万元,甲种存款的年利率为2.4%,乙种存款的年利率为4.6%,该家一年共得利息7800元.求甲、乙两种存款各是多少万元?设甲、乙两种存款各是x万元、y万元.根据题意列方程组,得
15.列二元一次方程组解应用题:
(1) 根据市场调查,常觉大盒装(每盒10粒)和小盒装(每盒6粒)两种产品的销售量(按盒计算)比为2:5.某藏药厂每天生产常觉7000粒,问应分装大、小盒两种产品各多少盒?
(2)*.某校七年级有三个班,甲班人数是乙数的1又2/5倍,乙班比丙少20%,甲班有56人,七年级共有多少人
(3)*. 某水库,有流入一定量的水不断地流进来,按现在的放水量,水库中的水可使用80天,但最近日益增加,流入量减少20%,按现在的放水量放水,只能使用60天,问现在的流入量和放水量分别为多少 .设每天流入的水量为X,放出的水量为Y,水库的蓄水量为a,
(4)*. 某校体操队和篮球队的人数是5:6,排球队的人数比体操队的人数2倍少5人,篮球队的人数与体操队的人数的3倍的和等于42人,求三种队各有多少人?
16.完成下面的探究过程:打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花多少钱?设打折前买1件A商品需要x元,买1件B商品需要y元.根据题意列方程组,得 解方程组,得
这就是说,打折前,买1件A商品需要_____元,买1件B商品需要_____元.因此,打折前,买500件A商品和500件B商品需要_____元.因此,买500件A商品和500件B商品,打折后比打折前可以少花_____元.
(专题一):二元一次方程(组)有关概念
1、二元一次方程(组)的识别:
下列方程组是二元一次方程组的是( )
A、;B、;C、;D、。
2、方程组的解:
方程组的解是( )
A. ;B.;C.;D.。
(专题二):利用二元一次方程组求字母系数的值
1 若单项式与是同类项,则的值是 .
2解方程组时,甲由于看错系数a,结果解得;乙由于看错系数b,结果解得,则原来的a=______,b=______.
(专题三):解二元一次方程组
1、求二元一次方程的整数解: 求方程2x+y=10的所有正整数解。
2、解二元一次方程组
解方程组
(专题四):二元一次方程组的应用
1、二元一次方程的应用:
小明口袋里有5角和1元的硬币若干枚,面值2.50元,问5角和1元的各有多少枚?
2、二元一次方程组的应用
1、 汶川大地震发生后,为了不担误孩子们的学习,一所所帐篷学校在废墟旁悄然兴起,热心的张老板知道这些孩子们的课作业本都被埋在了倒塌教室的瓦砾下,急需笔记本做作业,于是购买一批笔记本送到某个救灾点的帐篷学校,在分发时发现,如果每人分发放2本,则可剩余180本;如果每人分发放3本,则不足80本。问这所帐篷学校共有多少名孩子?张老板买了多少本笔记本?
2、为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
练习:
1、以为解的二元一次方程组是( );
A. ;B. ;C. ;D.
2、如果5=m+n是关于x、y的二元一次方程,则m= ,n= 。
3、已知是方程的一个解,那么的值是( )
A. B. C. D.
4、已知方程组的解是,则方程组的解是( )
(A) (B) (C) (D) 。
5、已知方程组的解也是方程x-y=1的一个解,则m的值是 ;
1、若,则的值为( )
A. B. C.0 D.4。
2、若与2是同类项,则a-b的值等于______.
4、如果关于x、y的方程组的解与的解相同,求a、b的值。
1、一个两位数,其十位上的数与个位上的数的和等于1,这个两位数是______.
2、求方程3x+7y=20的正整数解。3、解方程组。
1、四川大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷顶、乙种帐篷顶,那么下面列出的方程组中正确的是( )
A. B. ( http: / / ) C. D. ( http: / / )
课题:第八章二元一次方程组复习(1-2)
主备:代令 集体备课:张、龚 总课时:总第49.50课时
一、学习目标:
1. 知道第八章二元一次方程组知识结构图.
2.通过基本训练,巩固第八章所学的基本内容.
3.通过典型例题和综合运用,加深理解第八章所学的基本内容,发展能力.
二、学习重点和难点:
1.重点:知识结构图和基本训练.
2.难点:典型例题和综合运用.
三、归纳总结,完善认知:(阅读P117页及全章内容回答下列问题)
1.在方框内填写相应的文字
此框图说明什么 ___________________________________________________
四、基本训练,掌握双基
1.填空: (1)含有_____个未知数,并且含有未知数的项的次数都是_____,像这样的方程叫做二元一次方程.
(2)把具有相同未知数的两个二元一次方程合在一起,就组成了一个_________.
(3)既满足第一个二元一次方程,又满足第二个二元一次方程的两个未知数的值,叫做___________________.
(4)二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为我们熟悉的_______________方程,我们可以先求出一个未知数,然后再求另一个未知数.这种将未知数的个数由多化少、逐一解决的思想,叫做_________思想.
(5)把二元一次方程组中的一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做______________法,简称________法.
(6)两个二元一次方程中同一个未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去未知数,得到一个一元一次方程.这种方法叫做______________法,简称________法.
(7)用二元一次方程组解应用题一般有五步:________、设未知数、__________、解方程组、答.
2.在与两组值中,是二元一次方程组的解的是
3.完成下面的解题过程: 4.用代入法解方程组 用代入法解方程组
解:由①,得x=____________.③
把③代入②,得_______________.
解这个方程,得y=_____.
把y=_____代入③,得x=_____.
所以这个方程组的解是
5.完成下面的解题过程: 6.用加减法解方程组 用加减法解方程组
解: 解:①×3,得_________________.③
②+③,得________________.
x=______.
把x=______代入____,得__________,
y=______.
所以这个方程组的解是
7.解方程组
五、综合运用,发展能力
9. 2台大收割机和5台小收割机都工作2小时共收割青稞3.6公顷,3台大收割机和2台小收割机都工作5小时共收割青稞8公顷.1台大收割机和1台小收割机每小时各收割青稞多少公顷?
10.填空:已知二元一次方程组的解是,则m=_____,n=_____.
11.填空:某班学生共40人,男生比女生少3人,问男女生各多少人?设男生x人,女生y人.根据题意列方程组,得
12.填空:2本练习本及3支铅笔的价格为3.2元,4本练习本和5支铅笔的价格为5.8元.问一本练习本和一支铅笔的价格各为多少?设一本练习本的价格为x元,一支铅笔的价格为y元.根据题意列方程组,得
13.填空:某班上数学课的时候,准备分组讨论.如果每组7人,则余下3人;如果每组8人,则又不足5人.问全班有多少人?要分几组?设全班有x人,要分y组.根据题意列方程组,得
14.填空:某家存入银行甲、乙两种不同性质的存款20万元,甲种存款的年利率为2.4%,乙种存款的年利率为4.6%,该家一年共得利息7800元.求甲、乙两种存款各是多少万元?设甲、乙两种存款各是x万元、y万元.根据题意列方程组,得
15.列二元一次方程组解应用题:
(1) 根据市场调查,常觉大盒装(每盒10粒)和小盒装(每盒6粒)两种产品的销售量(按盒计算)比为2:5.某藏药厂每天生产常觉7000粒,问应分装大、小盒两种产品各多少盒?
(2)*.某校七年级有三个班,甲班人数是乙数的1又2/5倍,乙班比丙少20%,甲班有56人,七年级共有多少人
(3)*. 某水库,有流入一定量的水不断地流进来,按现在的放水量,水库中的水可使用80天,但最近日益增加,流入量减少20%,按现在的放水量放水,只能使用60天,问现在的流入量和放水量分别为多少 .设每天流入的水量为X,放出的水量为Y,水库的蓄水量为a,
(4)*. 某校体操队和篮球队的人数是5:6,排球队的人数比体操队的人数2倍少5人,篮球队的人数与体操队的人数的3倍的和等于42人,求三种队各有多少人?
16.完成下面的探究过程:打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花多少钱?设打折前买1件A商品需要x元,买1件B商品需要y元.根据题意列方程组,得 解方程组,得
这就是说,打折前,买1件A商品需要_____元,买1件B商品需要_____元.因此,打折前,买500件A商品和500件B商品需要_____元.因此,买500件A商品和500件B商品,打折后比打折前可以少花_____元.
(专题一):二元一次方程(组)有关概念
1、二元一次方程(组)的识别:
下列方程组是二元一次方程组的是( )
A、;B、;C、;D、。
2、方程组的解:
方程组的解是( )
A. ;B.;C.;D.。
(专题二):利用二元一次方程组求字母系数的值
1 若单项式与是同类项,则的值是 .
2解方程组时,甲由于看错系数a,结果解得;乙由于看错系数b,结果解得,则原来的a=______,b=______.
(专题三):解二元一次方程组
1、求二元一次方程的整数解: 求方程2x+y=10的所有正整数解。
2、解二元一次方程组
解方程组
(专题四):二元一次方程组的应用
1、二元一次方程的应用:
小明口袋里有5角和1元的硬币若干枚,面值2.50元,问5角和1元的各有多少枚?
2、二元一次方程组的应用
1、 汶川大地震发生后,为了不担误孩子们的学习,一所所帐篷学校在废墟旁悄然兴起,热心的张老板知道这些孩子们的课作业本都被埋在了倒塌教室的瓦砾下,急需笔记本做作业,于是购买一批笔记本送到某个救灾点的帐篷学校,在分发时发现,如果每人分发放2本,则可剩余180本;如果每人分发放3本,则不足80本。问这所帐篷学校共有多少名孩子?张老板买了多少本笔记本?
2、为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
练习:
1、以为解的二元一次方程组是( );
A. ;B. ;C. ;D.
2、如果5=m+n是关于x、y的二元一次方程,则m= ,n= 。
3、已知是方程的一个解,那么的值是( )
A. B. C. D.
4、已知方程组的解是,则方程组的解是( )
(A) (B) (C) (D) 。
5、已知方程组的解也是方程x-y=1的一个解,则m的值是 ;
1、若,则的值为( )
A. B. C.0 D.4。
2、若与2是同类项,则a-b的值等于______.
4、如果关于x、y的方程组的解与的解相同,求a、b的值。
1、一个两位数,其十位上的数与个位上的数的和等于1,这个两位数是______.
2、求方程3x+7y=20的正整数解。3、解方程组。
1、四川大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷顶、乙种帐篷顶,那么下面列出的方程组中正确的是( )
A. B. ( http: / / ) C. D. ( http: / / )
