苏教版小学数学六年级下册总复习:立体图形(共27张PPT)
文档属性
| 名称 | 苏教版小学数学六年级下册总复习:立体图形(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 24.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-03 20:19:56 | ||
图片预览


文档简介
(共27张PPT)
立体图形总复习(2)
点
线
面
表面积
体 积
整理与反思
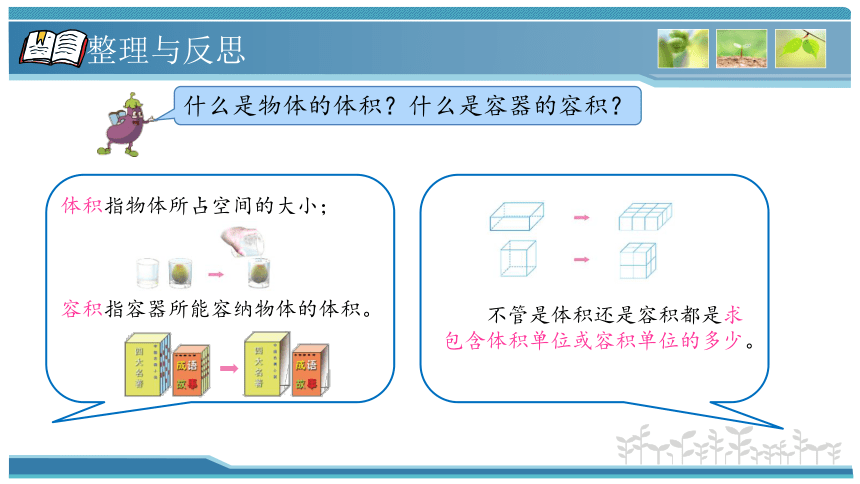
什么是物体的体积?什么是容器的容积?
整理与反思
体积指物体所占空间的大小;
容积指容器所能容纳物体的体积。
不管是体积还是容积都是求包含体积单位或容积单位的多少。
长 度
体 积
面 积
包含长度单位的多少
包含面积单位的多少
包含体积单位的多少
整理与反思
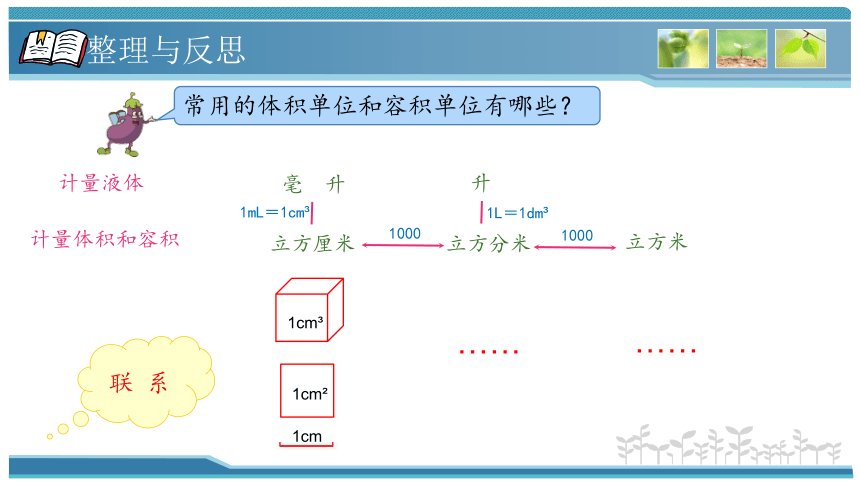
常用的体积单位和容积单位有哪些?
整理与反思
立方厘米
立方分米
立方米
1000
毫 升
升
计量体积和容积
计量液体
1cm
1cm
1cm
……
……
1000
1mL=1cm
1L=1dm
联 系
整理与反思
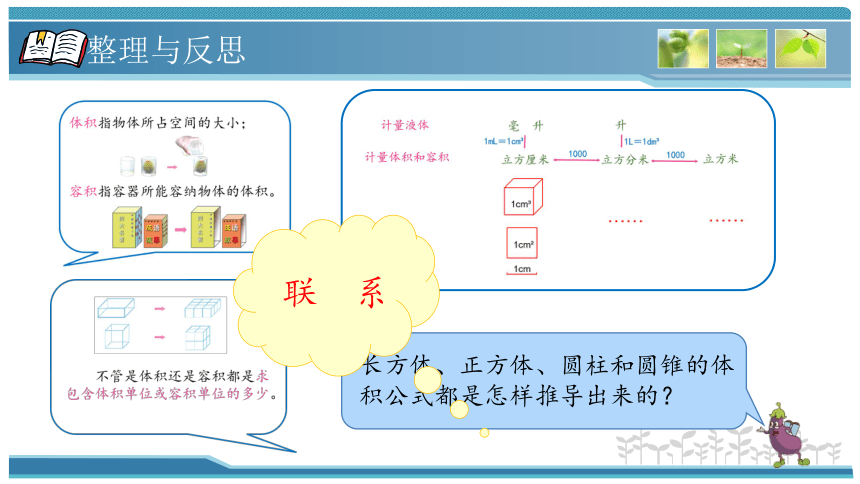
长方体、正方体、圆柱和圆锥的体积公式都是怎样推导出来的?
联 系
× ×
× ×
整理与反思
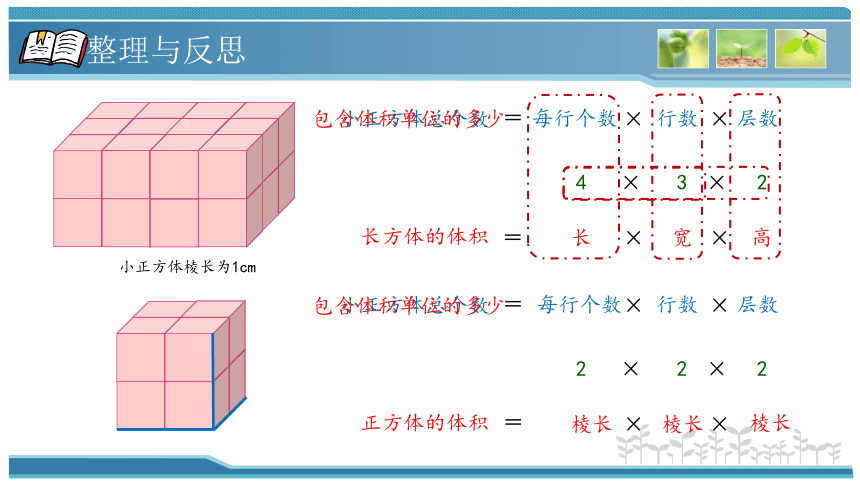
小正方体棱长为1cm
每行个数
行数
层数
4
3
2
小正方体总个数
长
宽
高
× ×
长方体的体积
=
包含体积单位的多少
=
× ×
× ×
行数
层数
2
2
2
小正方体总个数
× ×
棱长
棱长
棱长
正方体的体积
=
=
每行个数
包含体积单位的多少
整理与反思
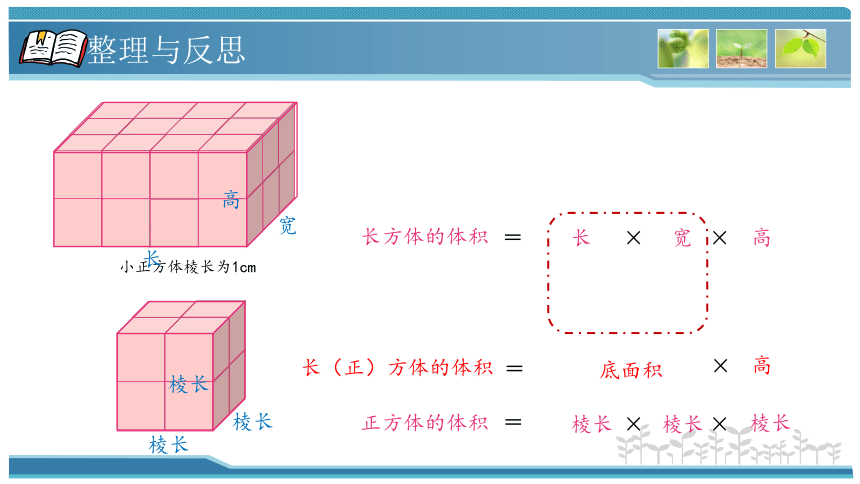
小正方体棱长为1cm
× ×
长
宽
高
长方体的体积
=
× ×
棱长
棱长
棱长
正方体的体积
=
高
×
长(正)方体的体积
=
底面积
长
宽
高
棱长
棱长
棱长
整理与反思
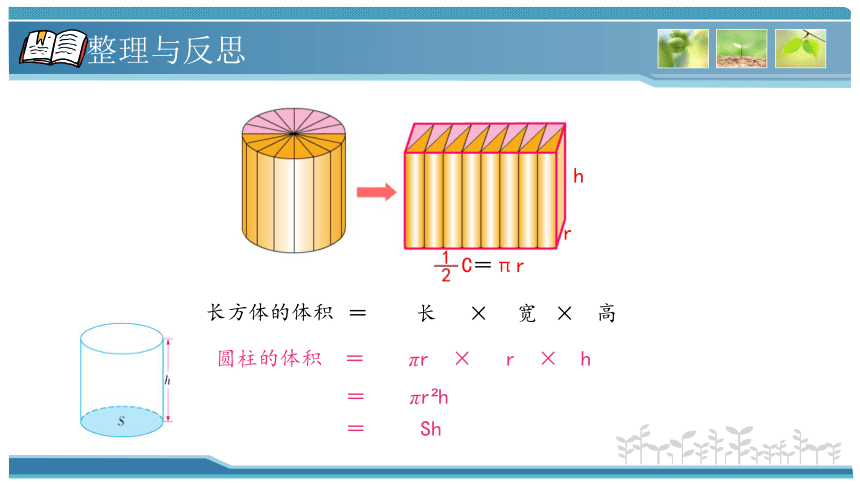
h
r
C=πr
× ×
长
宽
高
长方体的体积
=
圆柱的体积 = πr × r × h
= πr h
= Sh
整理与反思
3次正好倒满
圆锥的体积 = 底面积 × 高 ×
圆锥的体积是与它等底等高圆柱体积的 。
V = Sh
转 化
关 系
推 导
未知 已知
复杂 简单
整理与反思
这些体积计算公式之间有什么内在联系?
V = Sh
V=πr h
=Sh
V=abh
=Sh
V=a
=Sh
整理与反思
这些体积计算公式之间有什么内在联系?
统一
联 系
实践与拓展
你能试着用一张A4大小的长方形纸,做一个长方体或圆柱吗?(注意不进行裁剪。)按下暂停键,自己先试一试。
它们有什么不同和相同的地方?
高
底面周长
底面积
体积
不 同
侧面积
相 同
(长方形纸的面积)
底面周长=长
高=宽
底面周长=宽
高=长
实践与拓展
宽=高
长=高
比一比,这两个长方体一样吗?
有两个相对的面是正方形
相 同
侧面积=长方形纸的面积
你能试着用一张A4大小的长方形纸,做一个长方体或圆柱吗?(注意不进行裁剪。)按下暂停键,自己先试一试。
对折两次
实践与拓展
你能试着用一张A4大小的长方形纸,做一个长方体或圆柱吗?(注意不进行裁剪。)按下暂停键,自己先试一试。
实践与拓展
比一比,这些长方体有什么相同的地方?
侧面积相同
实践与拓展
这些长方体和圆柱之间有联系吗?
侧面积相同
实践与拓展
想一想,长方体、正方体和圆柱的侧面积能用统一的方法计算吗?
侧面积=底面周长×高
那表面积呢?
表面积=侧面积+底面积×2
实践与拓展
统一
练习与实践
1. 在括号里填合适的单位。
(1)一间卧室地面的面积是 15( )。
平方米
(2)一瓶牛奶大约有 250( )。
(3)一间教室的空间大约是 144( )。
(4)一台微波炉的体积是 92( ),容积是25( )。
毫升
立方米
立方分米
升
2.
0.5 m3 =( )dm3 4050 dm3 =( )m3
0.09 dm3 =( )cm3 60 cm3 =( )dm3
1.04 L =( )mL 75 mL =( )cm3
500
4.05
90
0.06
1040
75
数学书94页
选择单位
想清进率
练习与实践
数学书94页
熟练掌握
灵活运用
练习与实践
数学书95页
练习与实践
棱长
直径
练习与实践
制作这样一个油桶,至少需要多少铁皮?
表面积
侧面积+底面积×2
有关表面积的问题,还可能求……
游泳池
侧面积+底面积
侧面积
压路机压路的面积
一周商标纸
练习与实践
5.一个长方体金鱼缸,长40厘米,宽40厘米,高35厘米。它左侧面
的玻璃打碎了,要重新配一块。重新配上的玻璃是多少平方厘米?
是多少平方分米?
数学书95页
6.王冬家新买了一台柜式空调,它的外包装是一个长0.6米、宽0.4米、
高1.8米的长方体纸箱。 做这样一个纸箱至少需要硬纸板多少平方
米?(接头处忽略不计)
表面积
体 积
联 系
灵 活
统 一
同学们,再见!
立体图形总复习(2)
点
线
面
表面积
体 积
整理与反思
什么是物体的体积?什么是容器的容积?
整理与反思
体积指物体所占空间的大小;
容积指容器所能容纳物体的体积。
不管是体积还是容积都是求包含体积单位或容积单位的多少。
长 度
体 积
面 积
包含长度单位的多少
包含面积单位的多少
包含体积单位的多少
整理与反思
常用的体积单位和容积单位有哪些?
整理与反思
立方厘米
立方分米
立方米
1000
毫 升
升
计量体积和容积
计量液体
1cm
1cm
1cm
……
……
1000
1mL=1cm
1L=1dm
联 系
整理与反思
长方体、正方体、圆柱和圆锥的体积公式都是怎样推导出来的?
联 系
× ×
× ×
整理与反思
小正方体棱长为1cm
每行个数
行数
层数
4
3
2
小正方体总个数
长
宽
高
× ×
长方体的体积
=
包含体积单位的多少
=
× ×
× ×
行数
层数
2
2
2
小正方体总个数
× ×
棱长
棱长
棱长
正方体的体积
=
=
每行个数
包含体积单位的多少
整理与反思
小正方体棱长为1cm
× ×
长
宽
高
长方体的体积
=
× ×
棱长
棱长
棱长
正方体的体积
=
高
×
长(正)方体的体积
=
底面积
长
宽
高
棱长
棱长
棱长
整理与反思
h
r
C=πr
× ×
长
宽
高
长方体的体积
=
圆柱的体积 = πr × r × h
= πr h
= Sh
整理与反思
3次正好倒满
圆锥的体积 = 底面积 × 高 ×
圆锥的体积是与它等底等高圆柱体积的 。
V = Sh
转 化
关 系
推 导
未知 已知
复杂 简单
整理与反思
这些体积计算公式之间有什么内在联系?
V = Sh
V=πr h
=Sh
V=abh
=Sh
V=a
=Sh
整理与反思
这些体积计算公式之间有什么内在联系?
统一
联 系
实践与拓展
你能试着用一张A4大小的长方形纸,做一个长方体或圆柱吗?(注意不进行裁剪。)按下暂停键,自己先试一试。
它们有什么不同和相同的地方?
高
底面周长
底面积
体积
不 同
侧面积
相 同
(长方形纸的面积)
底面周长=长
高=宽
底面周长=宽
高=长
实践与拓展
宽=高
长=高
比一比,这两个长方体一样吗?
有两个相对的面是正方形
相 同
侧面积=长方形纸的面积
你能试着用一张A4大小的长方形纸,做一个长方体或圆柱吗?(注意不进行裁剪。)按下暂停键,自己先试一试。
对折两次
实践与拓展
你能试着用一张A4大小的长方形纸,做一个长方体或圆柱吗?(注意不进行裁剪。)按下暂停键,自己先试一试。
实践与拓展
比一比,这些长方体有什么相同的地方?
侧面积相同
实践与拓展
这些长方体和圆柱之间有联系吗?
侧面积相同
实践与拓展
想一想,长方体、正方体和圆柱的侧面积能用统一的方法计算吗?
侧面积=底面周长×高
那表面积呢?
表面积=侧面积+底面积×2
实践与拓展
统一
练习与实践
1. 在括号里填合适的单位。
(1)一间卧室地面的面积是 15( )。
平方米
(2)一瓶牛奶大约有 250( )。
(3)一间教室的空间大约是 144( )。
(4)一台微波炉的体积是 92( ),容积是25( )。
毫升
立方米
立方分米
升
2.
0.5 m3 =( )dm3 4050 dm3 =( )m3
0.09 dm3 =( )cm3 60 cm3 =( )dm3
1.04 L =( )mL 75 mL =( )cm3
500
4.05
90
0.06
1040
75
数学书94页
选择单位
想清进率
练习与实践
数学书94页
熟练掌握
灵活运用
练习与实践
数学书95页
练习与实践
棱长
直径
练习与实践
制作这样一个油桶,至少需要多少铁皮?
表面积
侧面积+底面积×2
有关表面积的问题,还可能求……
游泳池
侧面积+底面积
侧面积
压路机压路的面积
一周商标纸
练习与实践
5.一个长方体金鱼缸,长40厘米,宽40厘米,高35厘米。它左侧面
的玻璃打碎了,要重新配一块。重新配上的玻璃是多少平方厘米?
是多少平方分米?
数学书95页
6.王冬家新买了一台柜式空调,它的外包装是一个长0.6米、宽0.4米、
高1.8米的长方体纸箱。 做这样一个纸箱至少需要硬纸板多少平方
米?(接头处忽略不计)
表面积
体 积
联 系
灵 活
统 一
同学们,再见!
