人教版数学八年级下册 20.1.1平均数 课时2 课件(共31张)
文档属性
| 名称 | 人教版数学八年级下册 20.1.1平均数 课时2 课件(共31张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
人教版 八年级·下册
20.1.1 平均数 课时2
第二十章 数据的分析
时间:2022/6/2
1.算术平均数:一般地,如果有 n 个数 x1,x2,……xn,那么我们把(x1+x2+……+xn) 叫做这 n 个数的算术平均数,简称平均数,记作 ,则有 =(x1+x2+……+xn).
知识回顾
知识回顾
加权平均数:一般地,若 n 个数 x1,x2, , xn 的权分别是 w1,w2, , wn,那么我们把 叫做这 n 个数的加权平均数.
在求 n 个数的平均数时,如果 x1 出现 f1 次, x2 出现 f2 次,…… xk 出现 fk 次(这里的 f1+ f2+…… +fk =n),那么这 n 个数的平均数 = . 也叫做 x1,x2,……xk 这 k 个数的加权平均数, 其中 f1, f2,……. fk分别叫做 x1,x2,……xk 的权.
某汽车厂为了了解2000辆汽车的安全可靠性能,你认为下列方法是否可行,为什么?
1. 从中抽出15辆做碰撞试验;
2. 用抽取的15辆汽车的安全可靠性可以作为一个样本;
3. 用抽取的样本的安全可靠性来估计整批2000辆汽车的安全可靠性能.
导入新知
2.体会并理解用样本估计总体的统计思想.
1. 理解组中值的意义,能利用组中值计算一组数据的加权平均数 .
素养目标
新知探究
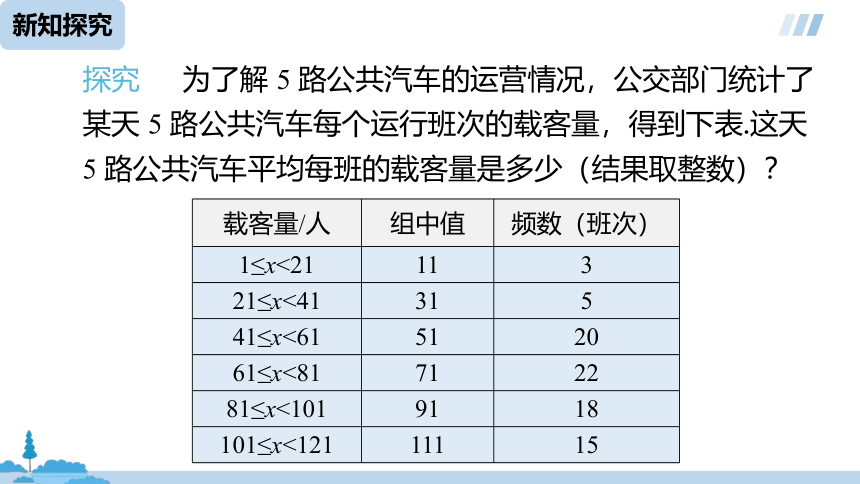
探究 为了解 5 路公共汽车的运营情况,公交部门统计了某天 5 路公共汽车每个运行班次的载客量,得到下表.这天 5 路公共汽车平均每班的载客量是多少(结果取整数)?
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
61≤x<81 71 22
81≤x<101 91 18
101≤x<121 111 15
新知探究
组中值是指数据分组后,一个小组的两个端点的数的平均数.统计中常以其代表各组的实际数据.
例如,小组 1≤x<21的组中值是.
频数 可以看作相应组中值的权.
思考1 表格中的组中值指什么?如何确定呢?
思考2 各组的频数可以看作什么?
知识点1:用组中值求平均数
新知探究
= ≈ 73(人)
频数分布表(图)中的加权平均数的求法:
①不同数据组中组中值的确定;
②权的确定.
答:这天5路公共汽车平均每班的载客量是73人.
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f1, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器求平均数的方法:
探究新知
分 数 段 组中值 人 数
40≤x<60 2
60≤x<80 8
80≤x<100 10
100≤x≤120 20
问班级平均分约是多少?
1.某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
巩固练习
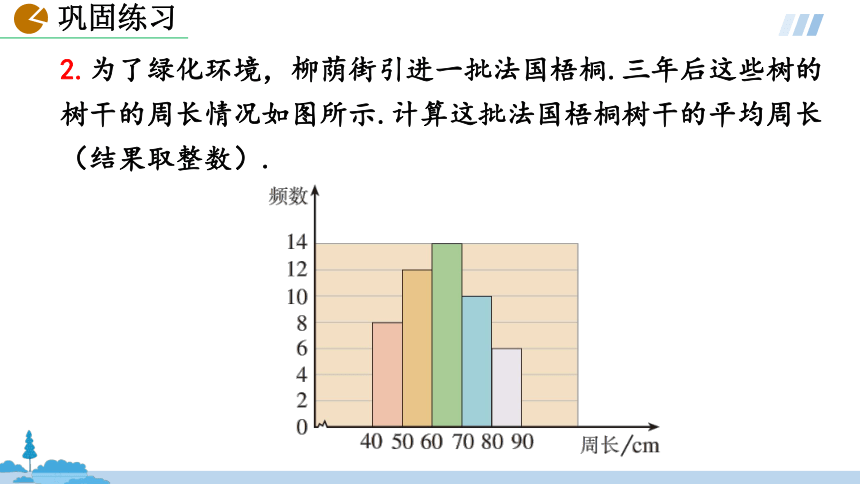
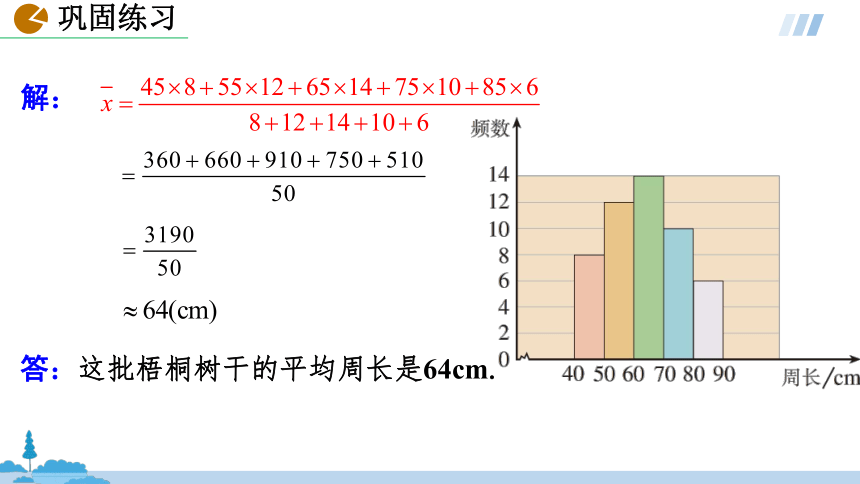
2.为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
巩固练习
答:这批梧桐树干的平均周长是64cm.
巩固练习
解:
果园里有100 棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?
每个梨的质量?
探究新知
知识点 2
利用样本估计总体平均数
所以平均每棵梨树上梨的个数为154.
(1)果农从100 棵梨树中任意选出10 棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
探究新知
梨的质量 x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
12
16
8
(2)果农从这10 棵梨树的每一棵树上分别随机摘4个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以平均每个梨的质量约为0.42 kg.
探究新知
(kg).
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
【思考】这个生活中的问题是如何解决的,体现了怎
样的统计思想?
所以该果园中梨的总产量约为6468 kg.
探究新知
(kg).
新知探究
知识点2:利用样本估计总体
用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
例 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
探究新知
素养考点 1
利用样本估计求平均数
答:即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是1 672 h.
样本估计总体
探究新知
解:据上表得各小组的组中值,于是
(h)
知识拓展
(1)一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也越精确,但相应的工作量也越大.因此在实际工作中,样本容量的确定既要考虑问题本身的需要,又要考虑实现的可能性及成本;
(2)抽取的样本要有随机性和代表性,这样有利于
估计总体,解决问题.
1.为了检查一批零件的质量,从中随机抽取了10 件,测得它们的长度分别为(单位:mm)15.0、15.1、15.4、15.0、15.5、15.2、15.2、15.1、15.5、15.3.根据以上数据,你能估计出这批零件的平均长度吗?
随堂练习
解:==15.23
样本的平均数为 15.23mm,所以这批零件的平均长度约为 15.23mm.
还有其他方法吗?
解: 15.0 的频数为 2,15.1 的频数为 2 , 15.2 的频数为 2 , 15.3 的频数为 1, 15.4 的频数为 1,15.5 的频数为 2.
随堂练习
= =15.23
方法二
还有其他方法吗?
15.0、15.1、15.4、15.0、15.5、15.2、15.2、15.1、15.5、15.3
课堂小结
样本估计总体
组中值
样本估计总体
组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
年 龄 频数
28≤x<30 4
30≤x<32 4
32≤x<34 8
34≤x<36 8
36≤x<38 12
38≤x<40 14
40≤x<42 6
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
随堂练习
2.某校为了解该校八年级男生的身高,随机抽查了50 名该校八年级男生的身高,经统计得到下表,估计该校八年级男生的平均身高是多少.
身高/cm 组中值 频数(人数)
140≤x<150 145 6
150≤x<160 155 35
160≤x<170 165 7
170≤x<180 175 2
随堂练习
解析:由表中的组中值及加权平均数公式得
= =156(cm)
估计该校八年级男生的平均身高为 156cm.
随堂练习
拓展提升
3.某校为了预测本校九年级男生的体育测试达标情况,随机抽取了部分男生进行了一次模拟测试(满分为 50 分,成绩均记为整数分),并按此时成绩 a(单位:分)分成四个档次:A 类(45拓展提升
A 类(45(1)求本次抽取的样本容量和扇形统计图中 A 类所对应的圆心角的度数;
(2)C 类学生共有多少人?若该校九年级男生共有 500 名,那么该校九年级男生毕业体育测试成绩能达标的有多少人( D 类测试成绩不达标)?
拓展提升
解:(1)A 类档次共计 10 人,占比 20%,则抽取的全部学生人数为 1020%=50 人.
所以抽取的样本容量为 50 人.
整个圆形为 360 ,A 类档次占其中的 20%,则圆心角为360 20%=72 .
拓展提升
(2)A 类档次共计 10 人, B 类档次共计 22 人, D 类档次共计 3 人,抽取的样本容量为 50 人,则 C 类档次共计15人.
D 类档次共计 3 人,抽取的样本容量为 50 人,样本中不达标的占比为 . 则总共 500 名学生,不达标的人数为 30人,也即达标的人数为 470人.
课后作业
请完成课本后练习第116页习题。
人教版 八年级·下册
20.1.1 平均数 课时2
第二十章 数据的分析
时间:2022/6/2
1.算术平均数:一般地,如果有 n 个数 x1,x2,……xn,那么我们把(x1+x2+……+xn) 叫做这 n 个数的算术平均数,简称平均数,记作 ,则有 =(x1+x2+……+xn).
知识回顾
知识回顾
加权平均数:一般地,若 n 个数 x1,x2, , xn 的权分别是 w1,w2, , wn,那么我们把 叫做这 n 个数的加权平均数.
在求 n 个数的平均数时,如果 x1 出现 f1 次, x2 出现 f2 次,…… xk 出现 fk 次(这里的 f1+ f2+…… +fk =n),那么这 n 个数的平均数 = . 也叫做 x1,x2,……xk 这 k 个数的加权平均数, 其中 f1, f2,……. fk分别叫做 x1,x2,……xk 的权.
某汽车厂为了了解2000辆汽车的安全可靠性能,你认为下列方法是否可行,为什么?
1. 从中抽出15辆做碰撞试验;
2. 用抽取的15辆汽车的安全可靠性可以作为一个样本;
3. 用抽取的样本的安全可靠性来估计整批2000辆汽车的安全可靠性能.
导入新知
2.体会并理解用样本估计总体的统计思想.
1. 理解组中值的意义,能利用组中值计算一组数据的加权平均数 .
素养目标
新知探究
探究 为了解 5 路公共汽车的运营情况,公交部门统计了某天 5 路公共汽车每个运行班次的载客量,得到下表.这天 5 路公共汽车平均每班的载客量是多少(结果取整数)?
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
61≤x<81 71 22
81≤x<101 91 18
101≤x<121 111 15
新知探究
组中值是指数据分组后,一个小组的两个端点的数的平均数.统计中常以其代表各组的实际数据.
例如,小组 1≤x<21的组中值是.
频数 可以看作相应组中值的权.
思考1 表格中的组中值指什么?如何确定呢?
思考2 各组的频数可以看作什么?
知识点1:用组中值求平均数
新知探究
= ≈ 73(人)
频数分布表(图)中的加权平均数的求法:
①不同数据组中组中值的确定;
②权的确定.
答:这天5路公共汽车平均每班的载客量是73人.
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f1, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器求平均数的方法:
探究新知
分 数 段 组中值 人 数
40≤x<60 2
60≤x<80 8
80≤x<100 10
100≤x≤120 20
问班级平均分约是多少?
1.某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
巩固练习
2.为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
巩固练习
答:这批梧桐树干的平均周长是64cm.
巩固练习
解:
果园里有100 棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?
每个梨的质量?
探究新知
知识点 2
利用样本估计总体平均数
所以平均每棵梨树上梨的个数为154.
(1)果农从100 棵梨树中任意选出10 棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
探究新知
梨的质量 x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
12
16
8
(2)果农从这10 棵梨树的每一棵树上分别随机摘4个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以平均每个梨的质量约为0.42 kg.
探究新知
(kg).
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
【思考】这个生活中的问题是如何解决的,体现了怎
样的统计思想?
所以该果园中梨的总产量约为6468 kg.
探究新知
(kg).
新知探究
知识点2:利用样本估计总体
用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
例 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
探究新知
素养考点 1
利用样本估计求平均数
答:即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是1 672 h.
样本估计总体
探究新知
解:据上表得各小组的组中值,于是
(h)
知识拓展
(1)一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也越精确,但相应的工作量也越大.因此在实际工作中,样本容量的确定既要考虑问题本身的需要,又要考虑实现的可能性及成本;
(2)抽取的样本要有随机性和代表性,这样有利于
估计总体,解决问题.
1.为了检查一批零件的质量,从中随机抽取了10 件,测得它们的长度分别为(单位:mm)15.0、15.1、15.4、15.0、15.5、15.2、15.2、15.1、15.5、15.3.根据以上数据,你能估计出这批零件的平均长度吗?
随堂练习
解:==15.23
样本的平均数为 15.23mm,所以这批零件的平均长度约为 15.23mm.
还有其他方法吗?
解: 15.0 的频数为 2,15.1 的频数为 2 , 15.2 的频数为 2 , 15.3 的频数为 1, 15.4 的频数为 1,15.5 的频数为 2.
随堂练习
= =15.23
方法二
还有其他方法吗?
15.0、15.1、15.4、15.0、15.5、15.2、15.2、15.1、15.5、15.3
课堂小结
样本估计总体
组中值
样本估计总体
组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
年 龄 频数
28≤x<30 4
30≤x<32 4
32≤x<34 8
34≤x<36 8
36≤x<38 12
38≤x<40 14
40≤x<42 6
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
随堂练习
2.某校为了解该校八年级男生的身高,随机抽查了50 名该校八年级男生的身高,经统计得到下表,估计该校八年级男生的平均身高是多少.
身高/cm 组中值 频数(人数)
140≤x<150 145 6
150≤x<160 155 35
160≤x<170 165 7
170≤x<180 175 2
随堂练习
解析:由表中的组中值及加权平均数公式得
= =156(cm)
估计该校八年级男生的平均身高为 156cm.
随堂练习
拓展提升
3.某校为了预测本校九年级男生的体育测试达标情况,随机抽取了部分男生进行了一次模拟测试(满分为 50 分,成绩均记为整数分),并按此时成绩 a(单位:分)分成四个档次:A 类(45
A 类(45
(2)C 类学生共有多少人?若该校九年级男生共有 500 名,那么该校九年级男生毕业体育测试成绩能达标的有多少人( D 类测试成绩不达标)?
拓展提升
解:(1)A 类档次共计 10 人,占比 20%,则抽取的全部学生人数为 1020%=50 人.
所以抽取的样本容量为 50 人.
整个圆形为 360 ,A 类档次占其中的 20%,则圆心角为360 20%=72 .
拓展提升
(2)A 类档次共计 10 人, B 类档次共计 22 人, D 类档次共计 3 人,抽取的样本容量为 50 人,则 C 类档次共计15人.
D 类档次共计 3 人,抽取的样本容量为 50 人,样本中不达标的占比为 . 则总共 500 名学生,不达标的人数为 30人,也即达标的人数为 470人.
课后作业
请完成课本后练习第116页习题。
