人教版七年级下册9.2 一元一次不等式课件(共20张PPT)
文档属性
| 名称 | 人教版七年级下册9.2 一元一次不等式课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 07:01:44 | ||
图片预览








文档简介
(共20张PPT)
回忆什么是一元一次方程?
含有一个未知数,未知数的次数是1,等号两边
都是整式,这样的方程叫做一元一次方程。
温故知新
9.2 一元一次不等式
思考:观察下面的不等式,它们有哪些共同特征?
含有一个未知数,未知数次数是1的不等式,
叫做一元一次不等式.
一元一次不等式
(3)不等式两边都是整式
(1)每个不等式都只含有一个未知数
(2)未知数的次数都是1
探究新知
练习:下列式子中,哪些是一元一次不等式
(1) 3x + 2> x – 1 (2) 5x + 3 < 0
(3) (4) x ( x– 1) < 2x
左边不是整式
化简后是:x2 - x < 2 x
知识精炼
2. 已知 是关于x 的一元一次不等式,
则a的值是 ________.
1
知识精炼
解:
移 项
你还记得上节课我们是怎么解 x -7>26的吗?
x -7 + 7 > 26 + 7
x > 33
x > 26 + 7
你认为还有更简单的解法吗?
移项这种方法以前用过吗?
探究新知
变 号
例 解不等式:
2(1 + x) < 3
解方程:
2(1+x)=3
去括号
2 + 2x = 3
合并同类项
2x = 1
系数化为1
移 项
2x = 3 - 2
解:
2 + 2x < 3
2x < 1
2x < 3 - 2
这个不等式的解集在数轴上表示如图:
0
解:
去括号
移 项
合并同类项
系数化为1
“类比”的数学思想
典例解析
例 解下列不等式,并在数轴上表示解集:
解:
去分母
去括号
移项
合并同类项
系数化为1
这个不等式的解集表示在数轴上如图:
0
3(2 + x )≥ 2(2x-1)
6 + 3x ≥ 4x-2
3x-4x ≥-2-6
-x ≥ -8
x≤ 8
8
典例解析
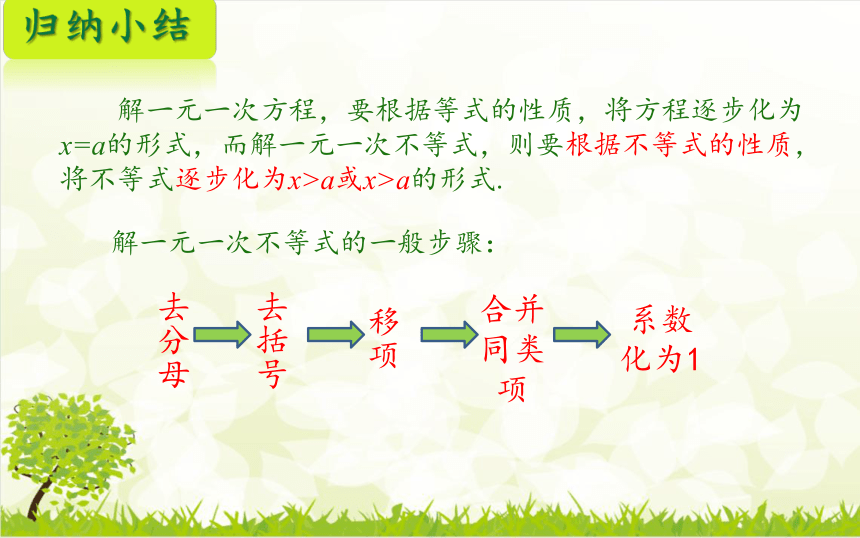
解一元一次不等式的一般步骤:
去分母
去括号
移项
合并
同类
项
系数化为1
归纳小结
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式,而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x>a或x>a的形式.
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解:(1)5x + 15 > 4x -1
x >-16
0
-16
解下列不等式 ,并在数轴上表示解集:
所以,这个不等式的解集在数轴上表示如图:
学以致用
(3) <
(4) ≥
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解下列不等式 ,并在数轴上表示解集:
学以致用
(3) <
(4) ≥
解:(2)2x + 10 ≤ 3x - 15
2x-3x ≤ -15- 10
-x ≤-25
x ≥ 25
25
0
这个不等式的解集表示是在数轴上如图:
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解下列不等式 ,并在数轴上表示解集:
学以致用
(3) <
(4) ≥
这个不等式的解集表示是在数轴上如图:
解:(3)3(x -1)< 7(2x + 5)
3x - 14x < 35 + 3
-11x < 38
3x - 3 < 14x + 35
x >
0
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解下列不等式 ,并在数轴上表示解集:
学以致用
(3) <
(4) ≥
所以,这个不等式的解集表示是在数轴上如图:
解:(4)4(x + 1)≥ 6(2x-5)+24
4x -12x ≥ -30 + 24-4
-8x ≥ -10
x ≤
4x + 4 ≥ 12x-30 + 24
0
课堂小结
1.定义:含有一个未知数,未知数次数是1的不等式,叫做一元一次不等式.
2.解一元一次不等式的一般步骤:
去分母
去括号
移项
合并
同类
项
系数化为1
B
1.若代数式 的值是非负数,则x 的取值
范围是( )
A.x ≥ B.x ≥
C. x> D.x >
学以致用
2.求不等式 的最大整数解。
所以,最大整数解为:0
0
1
变式:求不等式 的非负整数解。
0
5
所以,非负整数解为: 0、1、2、3、4、5
学以致用
3. 能力提升:已知不等式 x+8> 4x+m (m是常数)的解集是
x<3,求 m.
解: x+8 > 4x + m
x-4x > m-8
-3x>m-8
因为其解集为 x< 3
所以
m= -1
学以致用
下面是某同学解不等式 的过程:
解:去分母,得
移项,合并同类项,得
系数化为1,得
去括号,得
他的过程有错误吗?如果有错误,请你改过来。
学以致用
小
结
解一元一次不等式的一般步骤
01
去分母
02
去括号
03
移项
04
合并
同类
项
05
系数化为1
1.分子为多项式时要添括号
2.不要漏乘
1.不要漏乘
2.注意符号
移项要变号
合并系数注意符号
注意不等号的方向是否需要改变.
例:某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V 的取值范围.
典例精析
解:
V + 3×5×3 ≤ 3×5×10
根据题意:V的取值范围是 0 ≤ V ≤105
V ≤ 105
0
105
回忆什么是一元一次方程?
含有一个未知数,未知数的次数是1,等号两边
都是整式,这样的方程叫做一元一次方程。
温故知新
9.2 一元一次不等式
思考:观察下面的不等式,它们有哪些共同特征?
含有一个未知数,未知数次数是1的不等式,
叫做一元一次不等式.
一元一次不等式
(3)不等式两边都是整式
(1)每个不等式都只含有一个未知数
(2)未知数的次数都是1
探究新知
练习:下列式子中,哪些是一元一次不等式
(1) 3x + 2> x – 1 (2) 5x + 3 < 0
(3) (4) x ( x– 1) < 2x
左边不是整式
化简后是:x2 - x < 2 x
知识精炼
2. 已知 是关于x 的一元一次不等式,
则a的值是 ________.
1
知识精炼
解:
移 项
你还记得上节课我们是怎么解 x -7>26的吗?
x -7 + 7 > 26 + 7
x > 33
x > 26 + 7
你认为还有更简单的解法吗?
移项这种方法以前用过吗?
探究新知
变 号
例 解不等式:
2(1 + x) < 3
解方程:
2(1+x)=3
去括号
2 + 2x = 3
合并同类项
2x = 1
系数化为1
移 项
2x = 3 - 2
解:
2 + 2x < 3
2x < 1
2x < 3 - 2
这个不等式的解集在数轴上表示如图:
0
解:
去括号
移 项
合并同类项
系数化为1
“类比”的数学思想
典例解析
例 解下列不等式,并在数轴上表示解集:
解:
去分母
去括号
移项
合并同类项
系数化为1
这个不等式的解集表示在数轴上如图:
0
3(2 + x )≥ 2(2x-1)
6 + 3x ≥ 4x-2
3x-4x ≥-2-6
-x ≥ -8
x≤ 8
8
典例解析
解一元一次不等式的一般步骤:
去分母
去括号
移项
合并
同类
项
系数化为1
归纳小结
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式,而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x>a或x>a的形式.
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解:(1)5x + 15 > 4x -1
x >-16
0
-16
解下列不等式 ,并在数轴上表示解集:
所以,这个不等式的解集在数轴上表示如图:
学以致用
(3) <
(4) ≥
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解下列不等式 ,并在数轴上表示解集:
学以致用
(3) <
(4) ≥
解:(2)2x + 10 ≤ 3x - 15
2x-3x ≤ -15- 10
-x ≤-25
x ≥ 25
25
0
这个不等式的解集表示是在数轴上如图:
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解下列不等式 ,并在数轴上表示解集:
学以致用
(3) <
(4) ≥
这个不等式的解集表示是在数轴上如图:
解:(3)3(x -1)< 7(2x + 5)
3x - 14x < 35 + 3
-11x < 38
3x - 3 < 14x + 35
x >
0
(1)5x + 15 > 4x -1 (2)2(x + 5 )≤ 3(x - 5 )
解下列不等式 ,并在数轴上表示解集:
学以致用
(3) <
(4) ≥
所以,这个不等式的解集表示是在数轴上如图:
解:(4)4(x + 1)≥ 6(2x-5)+24
4x -12x ≥ -30 + 24-4
-8x ≥ -10
x ≤
4x + 4 ≥ 12x-30 + 24
0
课堂小结
1.定义:含有一个未知数,未知数次数是1的不等式,叫做一元一次不等式.
2.解一元一次不等式的一般步骤:
去分母
去括号
移项
合并
同类
项
系数化为1
B
1.若代数式 的值是非负数,则x 的取值
范围是( )
A.x ≥ B.x ≥
C. x> D.x >
学以致用
2.求不等式 的最大整数解。
所以,最大整数解为:0
0
1
变式:求不等式 的非负整数解。
0
5
所以,非负整数解为: 0、1、2、3、4、5
学以致用
3. 能力提升:已知不等式 x+8> 4x+m (m是常数)的解集是
x<3,求 m.
解: x+8 > 4x + m
x-4x > m-8
-3x>m-8
因为其解集为 x< 3
所以
m= -1
学以致用
下面是某同学解不等式 的过程:
解:去分母,得
移项,合并同类项,得
系数化为1,得
去括号,得
他的过程有错误吗?如果有错误,请你改过来。
学以致用
小
结
解一元一次不等式的一般步骤
01
去分母
02
去括号
03
移项
04
合并
同类
项
05
系数化为1
1.分子为多项式时要添括号
2.不要漏乘
1.不要漏乘
2.注意符号
移项要变号
合并系数注意符号
注意不等号的方向是否需要改变.
例:某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V 的取值范围.
典例精析
解:
V + 3×5×3 ≤ 3×5×10
根据题意:V的取值范围是 0 ≤ V ≤105
V ≤ 105
0
105
