人教版九年级上册24.2.2 直线和圆的位置关系课件(共17张PPT)
文档属性
| 名称 | 人教版九年级上册24.2.2 直线和圆的位置关系课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 17:00:04 | ||
图片预览


文档简介
(共17张PPT)
第二十四章 圆
24.2.2直线和圆的位置关系
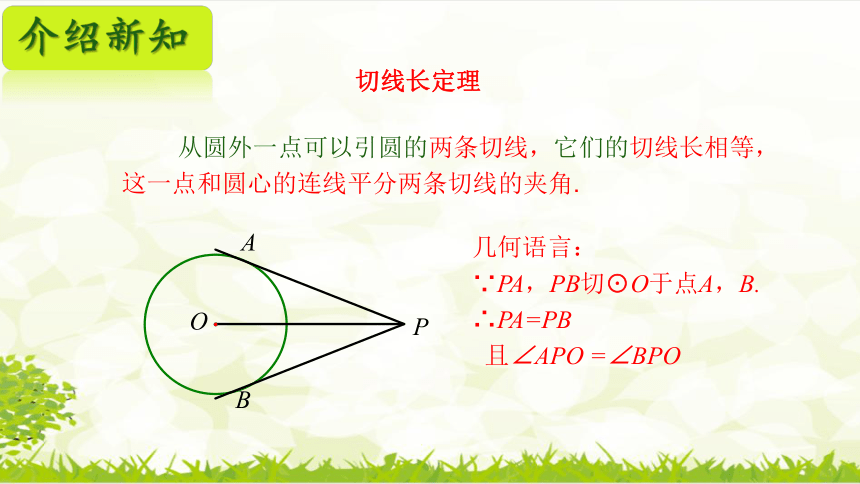
切线长定理
新人教版数学九年级上册
1. 探究切线长定理
2. 会运用切线长定理解决一些问题
3. 体会数形结合的思想和数学的对称美
学习目标
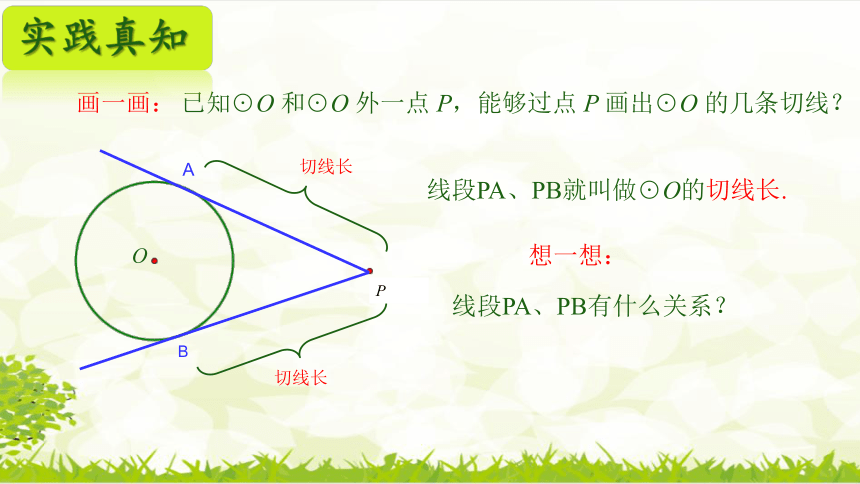
已知 O 和 O 外一点 P,能够过点 P 画出 O 的几条切线?
A
B
切线长
切线长
画一画:
P
实践真知
线段PA、PB就叫做 O的切线长.
想一想:
线段PA、PB有什么关系?
O
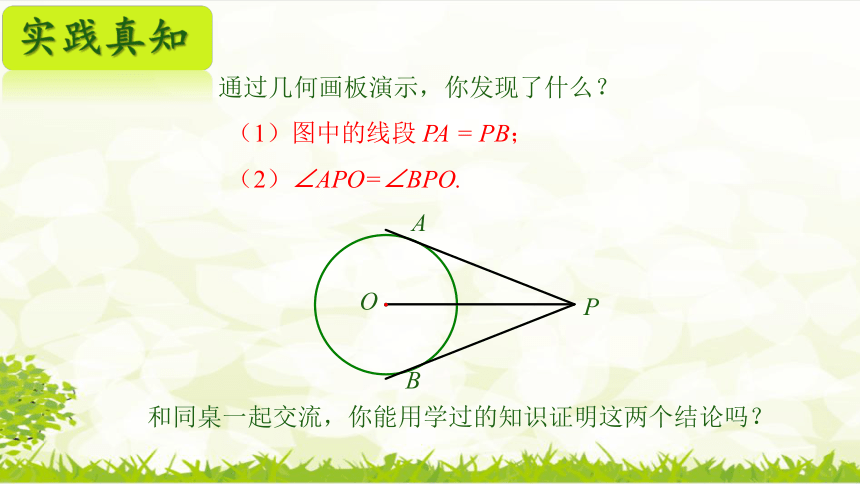
(1)图中的线段 PA = PB;
P
O
A
B
(2)∠APO=∠BPO.
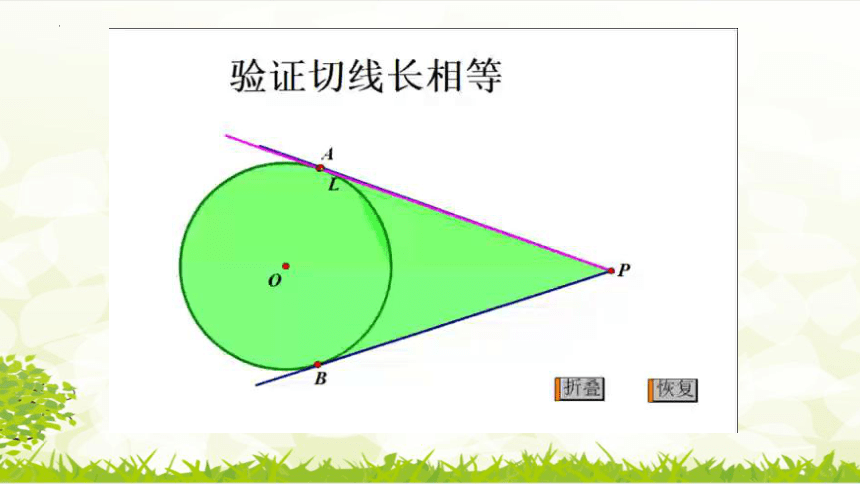
通过几何画板演示,你发现了什么?
实践真知
和同桌一起交流,你能用学过的知识证明这两个结论吗?
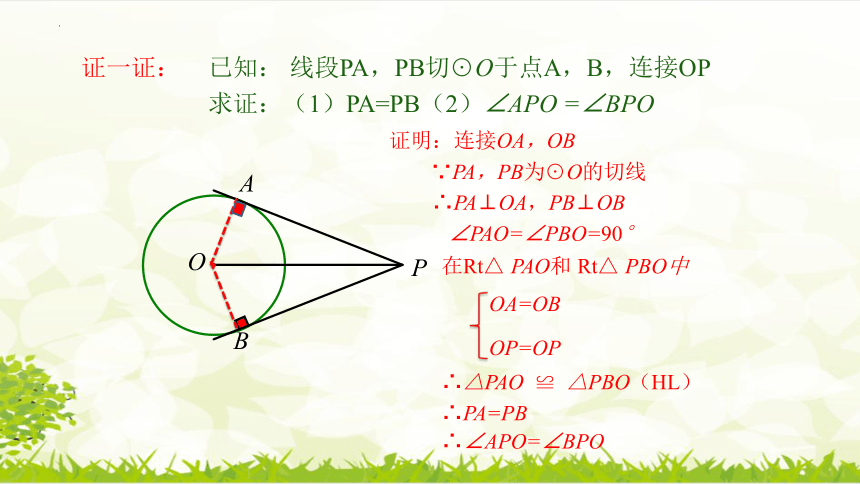
证明:连接OA,OB
∵PA,PB为 O的切线
∴PA⊥OA,PB⊥OB
∠PAO=∠PBO=90°
已知: 线段PA,PB切 O于点A,B,连接OP
求证:(1)PA=PB(2)∠APO =∠BPO
P
O
A
B
在Rt△ PAO和 Rt△ PBO中
∴△PAO ≌ △PBO(HL)
∴PA=PB
∴∠APO=∠BPO
OA=OB
OP=OP
证一证:
切线长定理
P
O
A
B
几何语言:
∵PA,PB切 O于点A,B.
∴PA=PB
且∠APO =∠BPO
介绍新知
从圆外一点可以引圆的两条切线,它们的切线长相等,
这一点和圆心的连线平分两条切线的夹角.
想一想:如图是一块三角形铁皮,工人师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
与三角形各边都相切的圆叫三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,
叫做三角形的内心.
O
已知: △ABC(如图)
求作:△ABC的内切圆.
A
B
C
分析:利用三角形的内心是三角形角平分线的交点,到三角形三边的距离相等,由此可确定半径,从而确定内切圆.
D
画一画:
●
例 △ABC的内切圆⊙O与BC,CA,AB分别相切于点 D,E,F,且AB = 9cm,BC = 14cm,CA = 13cm,求 AF,BD,CE 的长.
典例分析
解:设 AF = x,则 AE = x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x
由BD+CD=BC,可得
(13-x)+(9-x)=14
解得 x=4.
因此 AF=4,BD=5,CE=9.
9cm
14cm
13cm
1.如图:PA,PB是⊙O 的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
A. 60° B. 90°
C. 120° D. 150°
C
学以致用
2.如图,PA,PB分别切⊙O于A,B,PA = 5,过点C作⊙O的切线,则△PDE的周长为______.
10
D
C
E
O
P
A
B
学以致用
3.如图,⊙O与边长为2的正方形ABCD各边都相切,EF切⊙O于点P,交AB,BC于E,F,则△BEF的周长为_________
2
D
C
A
B
O
E
F
P
M
N
学以致用
4.如图所示PA、PB分别切圆O于A、B,并与圆O的切线CD分别
相交于C、D,如果∠P = 46°,则∠COD的度数是__________.
C
P
B
D
A
E
67°
学以致用
· O
5.如图,如果PA,PB是⊙O的两条切线,A,B为切点,PA = 4cm, PD = 2cm,则半径OA的长为________.
3cm
学以致用
如图,P是⊙○外一点,PA,PB分别和⊙○切于A,B两点,C是弧AB上任意一点,过C作⊙○的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为( )
A. 12 B. 6 C. 8 D. 4
B
∴PA+PB=12
PA=PB
∴PA=PB=6
拓展应用
∵△PDE的周长为12
1.切线长定理:
课堂小结
2.三角形的内切圆:
三角形的内心:内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
P
O
A
B
几何语言:∵PA,PB切 O于点A,B.
∴PA=PB 且∠APO =∠BPO
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
O
A
B
C
●
与三角形的三边都相切的圆叫做三角形的内切圆.
第二十四章 圆
24.2.2直线和圆的位置关系
切线长定理
新人教版数学九年级上册
1. 探究切线长定理
2. 会运用切线长定理解决一些问题
3. 体会数形结合的思想和数学的对称美
学习目标
已知 O 和 O 外一点 P,能够过点 P 画出 O 的几条切线?
A
B
切线长
切线长
画一画:
P
实践真知
线段PA、PB就叫做 O的切线长.
想一想:
线段PA、PB有什么关系?
O
(1)图中的线段 PA = PB;
P
O
A
B
(2)∠APO=∠BPO.
通过几何画板演示,你发现了什么?
实践真知
和同桌一起交流,你能用学过的知识证明这两个结论吗?
证明:连接OA,OB
∵PA,PB为 O的切线
∴PA⊥OA,PB⊥OB
∠PAO=∠PBO=90°
已知: 线段PA,PB切 O于点A,B,连接OP
求证:(1)PA=PB(2)∠APO =∠BPO
P
O
A
B
在Rt△ PAO和 Rt△ PBO中
∴△PAO ≌ △PBO(HL)
∴PA=PB
∴∠APO=∠BPO
OA=OB
OP=OP
证一证:
切线长定理
P
O
A
B
几何语言:
∵PA,PB切 O于点A,B.
∴PA=PB
且∠APO =∠BPO
介绍新知
从圆外一点可以引圆的两条切线,它们的切线长相等,
这一点和圆心的连线平分两条切线的夹角.
想一想:如图是一块三角形铁皮,工人师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
与三角形各边都相切的圆叫三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,
叫做三角形的内心.
O
已知: △ABC(如图)
求作:△ABC的内切圆.
A
B
C
分析:利用三角形的内心是三角形角平分线的交点,到三角形三边的距离相等,由此可确定半径,从而确定内切圆.
D
画一画:
●
例 △ABC的内切圆⊙O与BC,CA,AB分别相切于点 D,E,F,且AB = 9cm,BC = 14cm,CA = 13cm,求 AF,BD,CE 的长.
典例分析
解:设 AF = x,则 AE = x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x
由BD+CD=BC,可得
(13-x)+(9-x)=14
解得 x=4.
因此 AF=4,BD=5,CE=9.
9cm
14cm
13cm
1.如图:PA,PB是⊙O 的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
A. 60° B. 90°
C. 120° D. 150°
C
学以致用
2.如图,PA,PB分别切⊙O于A,B,PA = 5,过点C作⊙O的切线,则△PDE的周长为______.
10
D
C
E
O
P
A
B
学以致用
3.如图,⊙O与边长为2的正方形ABCD各边都相切,EF切⊙O于点P,交AB,BC于E,F,则△BEF的周长为_________
2
D
C
A
B
O
E
F
P
M
N
学以致用
4.如图所示PA、PB分别切圆O于A、B,并与圆O的切线CD分别
相交于C、D,如果∠P = 46°,则∠COD的度数是__________.
C
P
B
D
A
E
67°
学以致用
· O
5.如图,如果PA,PB是⊙O的两条切线,A,B为切点,PA = 4cm, PD = 2cm,则半径OA的长为________.
3cm
学以致用
如图,P是⊙○外一点,PA,PB分别和⊙○切于A,B两点,C是弧AB上任意一点,过C作⊙○的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为( )
A. 12 B. 6 C. 8 D. 4
B
∴PA+PB=12
PA=PB
∴PA=PB=6
拓展应用
∵△PDE的周长为12
1.切线长定理:
课堂小结
2.三角形的内切圆:
三角形的内心:内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
P
O
A
B
几何语言:∵PA,PB切 O于点A,B.
∴PA=PB 且∠APO =∠BPO
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
O
A
B
C
●
与三角形的三边都相切的圆叫做三角形的内切圆.
同课章节目录
