人教版七年级数学下册 9.3解含参数的一元一次不等式(组)— 解集的边界问题课件(共21张PPT)
文档属性
| 名称 | 人教版七年级数学下册 9.3解含参数的一元一次不等式(组)— 解集的边界问题课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 18:07:29 | ||
图片预览






文档简介
(共21张PPT)
解含参数的一元一次不等式(组)
—(1)解集的边界问题
PART 01
已知解集求参数的取值范围
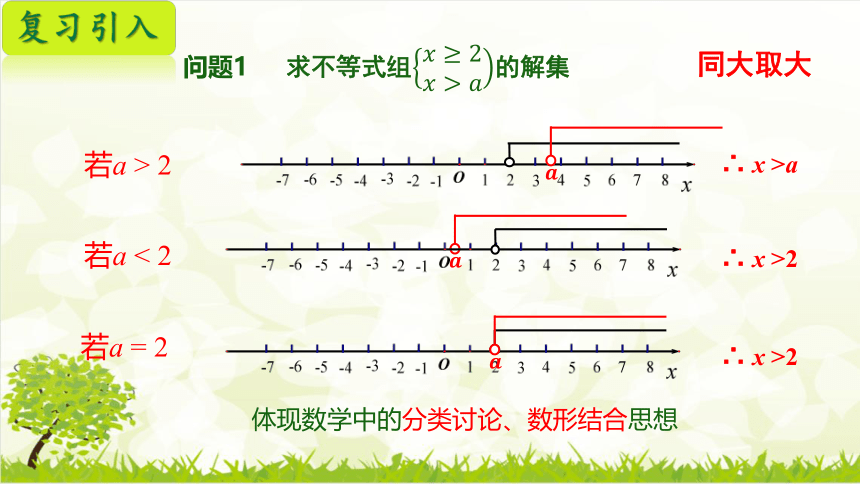
问题1 求不等式组的解集
同大取大
若a > 2
∴ x >a
∴ x >2
若a < 2
若a = 2
∴ x >2
复习引入
体现数学中的分类讨论、数形结合思想
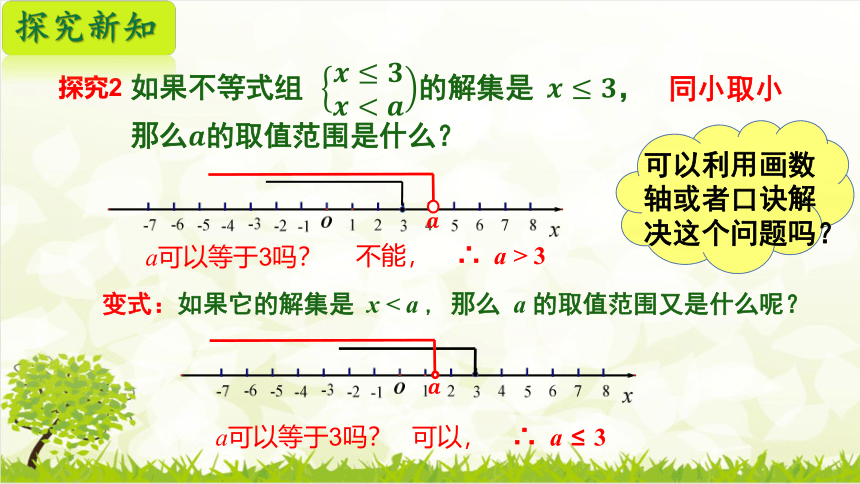
反过来,如果不等式组 的解集是 ,
那么的取值范围是什么?
可以利用画数轴或者口诀解决这个问题吗?
同大取大
∴ a ≤ 2
a可以等于2吗?
变式:如果它的解集是 x>a,那么a的取值范围又是什么呢?
a可以等于2吗?
∴ a ≥ 2
探究1
探究新知
x>a
x>2
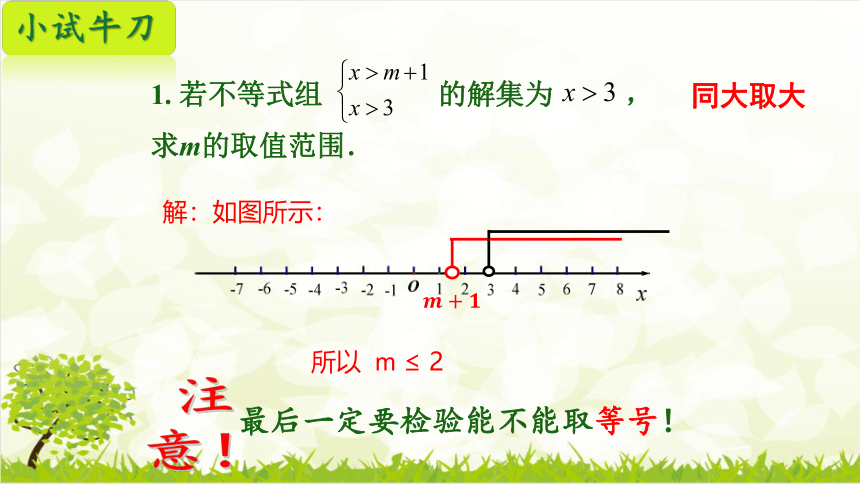
1. 若不等式组 的解集为 ,
求m的取值范围.
注
意!
最后一定要检验能不能取等号!
解:如图所示:
所以 m ≤ 2
同大取大
小试牛刀
如果不等式组的解集是 ,
那么的取值范围是什么?
可以利用画数轴或者口诀解决这个问题吗?
同小取小
不能, ∴ a > 3
变式:如果它的解集是 x < a , 那么 a 的取值范围又是什么呢?
a可以等于3吗?
a可以等于3吗?
可以, ∴ a ≤ 3
探究2
探究新知
2. 如果不等式组 的解集为 ,
则m的取值范围是( )
A. B.
C. D.
同小取小
m
D
小试牛刀
归纳小结
1.画数轴 2.用口诀 3.定参数位置 4.定参数范围
已知解集求参数取值范围的一般步骤:
大小小大取中间
如果不等式组无解,那么的取值范围是什么?
变式:如果它有解,那么a的取值范围是什么?
大大小小取无解
a可以等于3吗?
不能,∴a > 3
a可以等于3吗?
可以,∴a ≤ 3
探究3
探究新知
3、如果不等式组 有解,则m的取值
范围是( )
A . B.
C. D.
大小小大取中间
m
C
小试牛刀
4、关于x的不等式组 无解,
则a的取值范围是 。
大大小小取无解
由①得:x≤3
由②得:x>a
a
a≥3
小试牛刀
PART 02
已知特殊解求参数的取值范围
例题:已知 中有且只有3个整数解,求a的取值范围.
①求解集
②画数轴
③确定整数解
④确定a的大概范围
⑤验证等号是否成立
∴ 2< x < a
典例分析
1. 若关于x的不等式组 有5个整数解, 求 a 的取值范围.
解:解不等式组为
①求解集
②画数轴
③确定整数解
④确定a的大概范围
⑤验证等号是否成立
小试牛刀
2、关于x的不等式 的非负整数解只有3个,则m的取值范围是 。
小试牛刀
3、关于x的不等式组 有解但无整数解,则 a 的
取值范围是
小试牛刀
课堂小结
2.已知特殊解求参数的取值范围
①画数轴 ②用口诀 ③定参数位置 ④定参数范围
1.已知解集求参数取值范围的一般步骤:
①画数轴 ②确定整数解 ③定参数大概范围 ④验证等号是否成立
问题1 如果,,那么不等式组的解集是什么?
同大取大
a = 2 呢?
a > 2 呢?
∴ x >2
∴ x >2
∴ x >a
问题2 如果,那么不等式组的解集是什么?
同小取小
如果 a>3 呢?
∴ x < a
∴ x ≤ 3
如果 a = 3 呢?
∴ x < 3
问题2 求不等式组的解集
∴ x ≤ 3
若a > 3
∴ x < a
若a < 3
若a = 3
∴ x < 3
同小取小
问题3 求不等式组 的解集是什么
若a > 3
大大小小取无解
若a< 3
大小小大取中间
∴ a≤ x ≤3
若a= 3
∴ x = 3
解含参数的一元一次不等式(组)
—(1)解集的边界问题
PART 01
已知解集求参数的取值范围
问题1 求不等式组的解集
同大取大
若a > 2
∴ x >a
∴ x >2
若a < 2
若a = 2
∴ x >2
复习引入
体现数学中的分类讨论、数形结合思想
反过来,如果不等式组 的解集是 ,
那么的取值范围是什么?
可以利用画数轴或者口诀解决这个问题吗?
同大取大
∴ a ≤ 2
a可以等于2吗?
变式:如果它的解集是 x>a,那么a的取值范围又是什么呢?
a可以等于2吗?
∴ a ≥ 2
探究1
探究新知
x>a
x>2
1. 若不等式组 的解集为 ,
求m的取值范围.
注
意!
最后一定要检验能不能取等号!
解:如图所示:
所以 m ≤ 2
同大取大
小试牛刀
如果不等式组的解集是 ,
那么的取值范围是什么?
可以利用画数轴或者口诀解决这个问题吗?
同小取小
不能, ∴ a > 3
变式:如果它的解集是 x < a , 那么 a 的取值范围又是什么呢?
a可以等于3吗?
a可以等于3吗?
可以, ∴ a ≤ 3
探究2
探究新知
2. 如果不等式组 的解集为 ,
则m的取值范围是( )
A. B.
C. D.
同小取小
m
D
小试牛刀
归纳小结
1.画数轴 2.用口诀 3.定参数位置 4.定参数范围
已知解集求参数取值范围的一般步骤:
大小小大取中间
如果不等式组无解,那么的取值范围是什么?
变式:如果它有解,那么a的取值范围是什么?
大大小小取无解
a可以等于3吗?
不能,∴a > 3
a可以等于3吗?
可以,∴a ≤ 3
探究3
探究新知
3、如果不等式组 有解,则m的取值
范围是( )
A . B.
C. D.
大小小大取中间
m
C
小试牛刀
4、关于x的不等式组 无解,
则a的取值范围是 。
大大小小取无解
由①得:x≤3
由②得:x>a
a
a≥3
小试牛刀
PART 02
已知特殊解求参数的取值范围
例题:已知 中有且只有3个整数解,求a的取值范围.
①求解集
②画数轴
③确定整数解
④确定a的大概范围
⑤验证等号是否成立
∴ 2< x < a
典例分析
1. 若关于x的不等式组 有5个整数解, 求 a 的取值范围.
解:解不等式组为
①求解集
②画数轴
③确定整数解
④确定a的大概范围
⑤验证等号是否成立
小试牛刀
2、关于x的不等式 的非负整数解只有3个,则m的取值范围是 。
小试牛刀
3、关于x的不等式组 有解但无整数解,则 a 的
取值范围是
小试牛刀
课堂小结
2.已知特殊解求参数的取值范围
①画数轴 ②用口诀 ③定参数位置 ④定参数范围
1.已知解集求参数取值范围的一般步骤:
①画数轴 ②确定整数解 ③定参数大概范围 ④验证等号是否成立
问题1 如果,,那么不等式组的解集是什么?
同大取大
a = 2 呢?
a > 2 呢?
∴ x >2
∴ x >2
∴ x >a
问题2 如果,那么不等式组的解集是什么?
同小取小
如果 a>3 呢?
∴ x < a
∴ x ≤ 3
如果 a = 3 呢?
∴ x < 3
问题2 求不等式组的解集
∴ x ≤ 3
若a > 3
∴ x < a
若a < 3
若a = 3
∴ x < 3
同小取小
问题3 求不等式组 的解集是什么
若a > 3
大大小小取无解
若a< 3
大小小大取中间
∴ a≤ x ≤3
若a= 3
∴ x = 3
