6分数的加法和减法整理和复习(课件)五年级下册数学人教版(共28张PPT)
文档属性
| 名称 | 6分数的加法和减法整理和复习(课件)五年级下册数学人教版(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 894.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 00:56:37 | ||
图片预览






文档简介
(共28张PPT)
第六单元
分数的加法和减法整理和复习
分数的加法和减法
同分母分数相加、减法
分数连加、连减的运算
异分母分数加、减法
分数加减混合运算
分数加减法简便计算
解决喝牛奶问题
1.分母不变,分子相加、减。
2.能约分的要约分。
同分母分数相加、减法
3.分数的连加连减按从左到右计算。
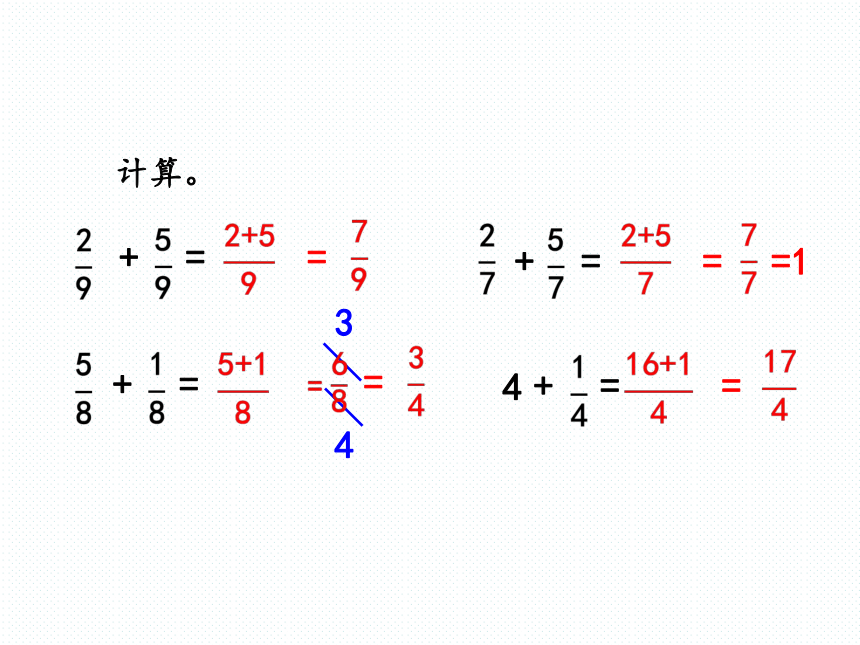
计算。
+
=
=
+
4
=
3
4
=
+
=
=
+
=
=1
=
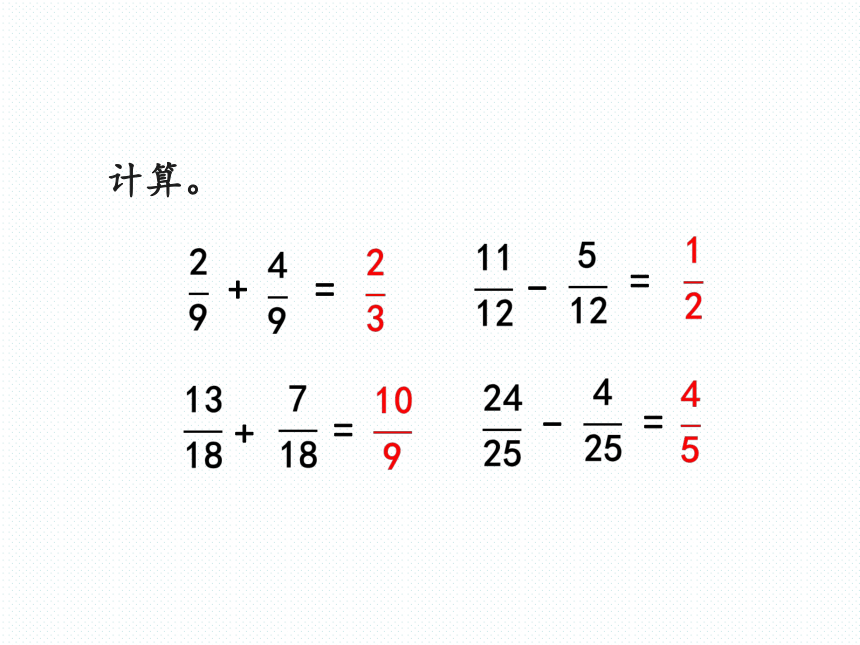
计算。
+
=
-
=
+
=
-
=
分数连加、连减的运算
分数连加、连减的运算顺序与整数一样,都是按从左到右来计算。
+
=
=
或
按照整数连加的计算顺序从左到右计算,也可以直接把每个加数的分子连加起来作分子,分母不变。
+
+
=
+
+
=
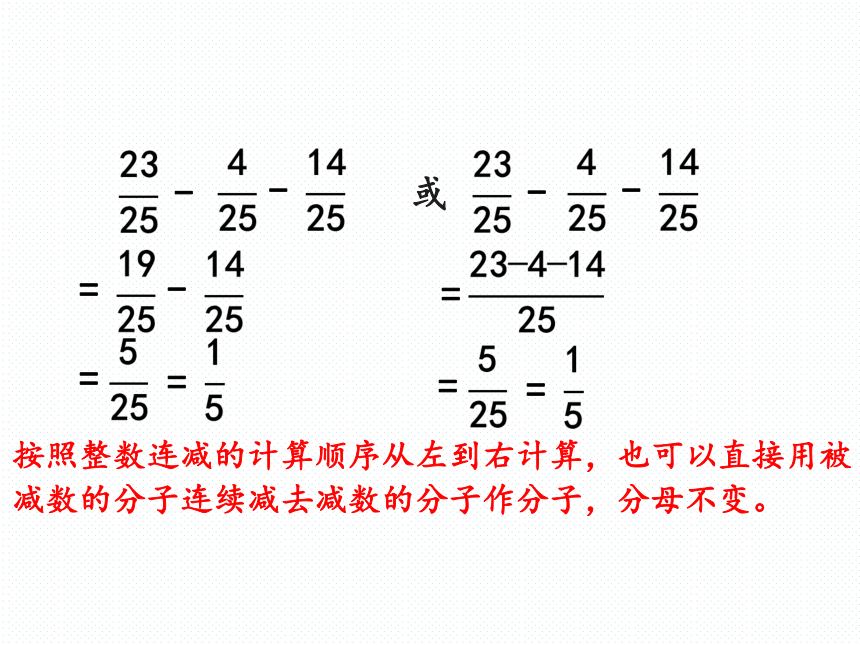
-
-
-
=
=
=
或
按照整数连减的计算顺序从左到右计算,也可以直接用被减数的分子连续减去减数的分子作分子,分母不变。
=
-
-
=
=
异分母分数加、减法
1.先通分。
2.再按照同分母分数加、减法进行计算。
3.能约分的要约分。
计算下列各题。
分数加减混合运算
运算顺序:没有括号的,按照从左到右的顺序依次计算。
方法:分步通分或一次性通分。
对比一下,发现了什么?
a-b-c=a-(b+c)
有括号先算括号。
计算。
计算。
列举法
集合法
分解质因数法
短除法
分数加减法简便计算
整数加法的交换律和结合律对分数加法同样适用,利用运算定律可以使一些分数计算变得简便。
用简便方法计算下面各题。
用简便方法计算下面各题。
1.运用画图法分析题意。
2.明确每次加的量和每次喝的量。
解决喝牛奶问题的步骤:
一共喝的纯牛奶:
一共喝的水:
(杯)
(杯)
加满水,
第二次又喝了半杯
一、填一填。
1.分数加法的意义与整数加法的意义( )。
2.同分母分数相加、减,分母不变,只把( )相加、减。
3.分母是9的最简真分数有( )个,它们的和是( )。
4.一根铁丝长4 m,平均分成5份,每份是( )m,每份占这根铁丝的( )。
5.异分母分数相加、减,要先( ),化成( )分数,再相加、减。
6.加工一批零件,王师傅需用10天完成,他平均每天完成这批零件的( ),3天完成这批零件的( )。
7.分子是3的假分数有( )个,它们的和是( )。
8.的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是1。
9.计算+时,因为它们的分母不同,也就是( )不同,所以要先( ),计算结果为( )。
二、判断。(对的画√,错的画×)
1.分数单位相同的分数才能相加、减。 ( )
2.分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同。 ( )
3.整数加法的交换律、结合律对分数加法不适用 ( )
4.一个最简分数,如果分母除了2和5以外,不含其他的质因数,这个分数就能化成有限小数。 ( )
5.1-+=1-1=0 ( )
三、选一选。(把正确答案的序号填在括号里)
1.+可以直接相加,是因为两个加数( )。
A.分子相同 B.分母相同 C.都是真分数 D.都是最简分数
2.王师傅做一项工作要20天完成,他做了5天,还剩下这项工作的( )没有完成。
A.4 B.19 C. D.
3.是假分数,a和b都是不为0的自然数,则a和b的关系是( )。
A.a大于b B.a小于b C.a等于b D.a大于或等于b
4.修路队修一条路,已经修了km,还剩下全长的。已经修的和剩下的长度相比,( )。
A.已经修的长 B.一样长 C.剩下的长 D.无法判断
4.计算。
用简便方法计算下面各题。
减号后加括号,括号里的加减运算符号要变成相反的哦。
五、解决问题。
1.一项工程,甲队单独完成要11天,乙队单独完成要15天,两队各做5天,一共完成这项工程的几分之几 还剩这项工程的几分之几没有完成
2.王彬看一本书,第一天看了全书的,第二天看了全书的。还剩下全书的几分之几没有看
3.一个长方形的长是m,宽是m,它的周长是多少米
4.一瓶饮料,喝去一半,又往瓶中加入L,这时瓶中的饮料比原来少L。这瓶饮料原有多少升
第六单元
分数的加法和减法整理和复习
分数的加法和减法
同分母分数相加、减法
分数连加、连减的运算
异分母分数加、减法
分数加减混合运算
分数加减法简便计算
解决喝牛奶问题
1.分母不变,分子相加、减。
2.能约分的要约分。
同分母分数相加、减法
3.分数的连加连减按从左到右计算。
计算。
+
=
=
+
4
=
3
4
=
+
=
=
+
=
=1
=
计算。
+
=
-
=
+
=
-
=
分数连加、连减的运算
分数连加、连减的运算顺序与整数一样,都是按从左到右来计算。
+
=
=
或
按照整数连加的计算顺序从左到右计算,也可以直接把每个加数的分子连加起来作分子,分母不变。
+
+
=
+
+
=
-
-
-
=
=
=
或
按照整数连减的计算顺序从左到右计算,也可以直接用被减数的分子连续减去减数的分子作分子,分母不变。
=
-
-
=
=
异分母分数加、减法
1.先通分。
2.再按照同分母分数加、减法进行计算。
3.能约分的要约分。
计算下列各题。
分数加减混合运算
运算顺序:没有括号的,按照从左到右的顺序依次计算。
方法:分步通分或一次性通分。
对比一下,发现了什么?
a-b-c=a-(b+c)
有括号先算括号。
计算。
计算。
列举法
集合法
分解质因数法
短除法
分数加减法简便计算
整数加法的交换律和结合律对分数加法同样适用,利用运算定律可以使一些分数计算变得简便。
用简便方法计算下面各题。
用简便方法计算下面各题。
1.运用画图法分析题意。
2.明确每次加的量和每次喝的量。
解决喝牛奶问题的步骤:
一共喝的纯牛奶:
一共喝的水:
(杯)
(杯)
加满水,
第二次又喝了半杯
一、填一填。
1.分数加法的意义与整数加法的意义( )。
2.同分母分数相加、减,分母不变,只把( )相加、减。
3.分母是9的最简真分数有( )个,它们的和是( )。
4.一根铁丝长4 m,平均分成5份,每份是( )m,每份占这根铁丝的( )。
5.异分母分数相加、减,要先( ),化成( )分数,再相加、减。
6.加工一批零件,王师傅需用10天完成,他平均每天完成这批零件的( ),3天完成这批零件的( )。
7.分子是3的假分数有( )个,它们的和是( )。
8.的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是1。
9.计算+时,因为它们的分母不同,也就是( )不同,所以要先( ),计算结果为( )。
二、判断。(对的画√,错的画×)
1.分数单位相同的分数才能相加、减。 ( )
2.分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同。 ( )
3.整数加法的交换律、结合律对分数加法不适用 ( )
4.一个最简分数,如果分母除了2和5以外,不含其他的质因数,这个分数就能化成有限小数。 ( )
5.1-+=1-1=0 ( )
三、选一选。(把正确答案的序号填在括号里)
1.+可以直接相加,是因为两个加数( )。
A.分子相同 B.分母相同 C.都是真分数 D.都是最简分数
2.王师傅做一项工作要20天完成,他做了5天,还剩下这项工作的( )没有完成。
A.4 B.19 C. D.
3.是假分数,a和b都是不为0的自然数,则a和b的关系是( )。
A.a大于b B.a小于b C.a等于b D.a大于或等于b
4.修路队修一条路,已经修了km,还剩下全长的。已经修的和剩下的长度相比,( )。
A.已经修的长 B.一样长 C.剩下的长 D.无法判断
4.计算。
用简便方法计算下面各题。
减号后加括号,括号里的加减运算符号要变成相反的哦。
五、解决问题。
1.一项工程,甲队单独完成要11天,乙队单独完成要15天,两队各做5天,一共完成这项工程的几分之几 还剩这项工程的几分之几没有完成
2.王彬看一本书,第一天看了全书的,第二天看了全书的。还剩下全书的几分之几没有看
3.一个长方形的长是m,宽是m,它的周长是多少米
4.一瓶饮料,喝去一半,又往瓶中加入L,这时瓶中的饮料比原来少L。这瓶饮料原有多少升
