4.1树与二叉树 课件-2021-2022学年浙教版(2019)高中信息技术选修1(28张PPT)
文档属性
| 名称 | 4.1树与二叉树 课件-2021-2022学年浙教版(2019)高中信息技术选修1(28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-06-04 08:34:04 | ||
图片预览






文档简介
(共28张PPT)
知识回顾
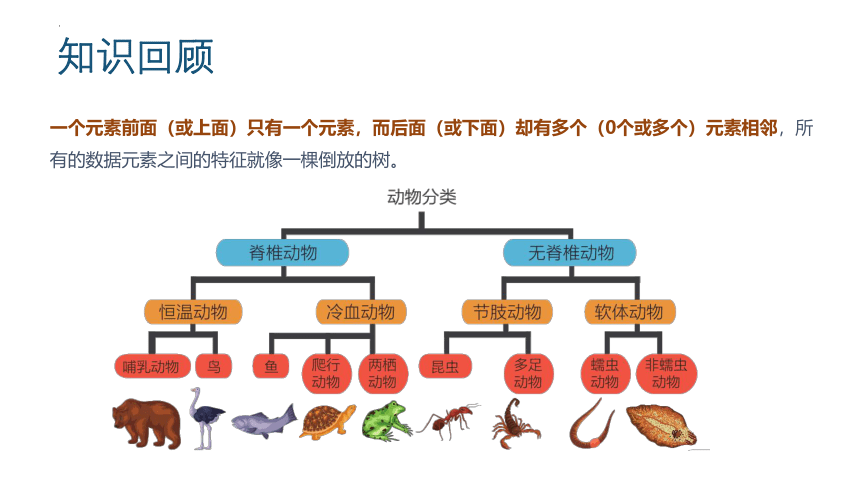
一个元素前面(或上面)只有一个元素,而后面(或下面)却有多个(0个或多个)元素相邻,所有的数据元素之间的特征就像一棵倒放的树。
CHZX
4.1树与二叉树
浙江省高中信息技术 选择性必修一 《数据与数据结构》
4.1.1 树
树的概念
树的基本术语
树的特性
01
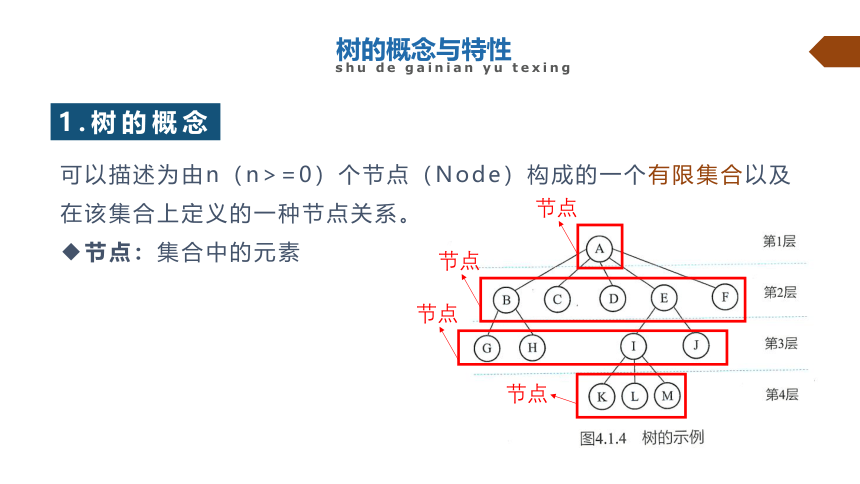
1.树的概念
可以描述为由n(n>=0)个节点(Node)构成的一个有限集合以及在该集合上定义的一种节点关系。
节点:集合中的元素
树的概念与特性
shu de gainian yu texing
节点
节点
节点
节点
2.树的基本术语
树的概念与特性
shu de gainian yu texing
节点
节点
节点
节点
节点:
根节点:
叶子节点:
分支节点:
父节点:
孩子节点:
边:
集合中的元素
(开始节点)没有前驱的节点
(终端节点)度为0的节点
除叶子节点以外的节点(内部节点:除根节点之外的分支节点)
(双亲节点)对于两个以边直接连接的节点中的上端节点
连接两个节点之间的线
对于两个以边直接连接的节点中的下端节点
2.树的基本术语
树的概念与特性
shu de gainian yu texing
节点:
根节点:
叶子节点:
分支节点:
父节点:
孩子节点:
边:
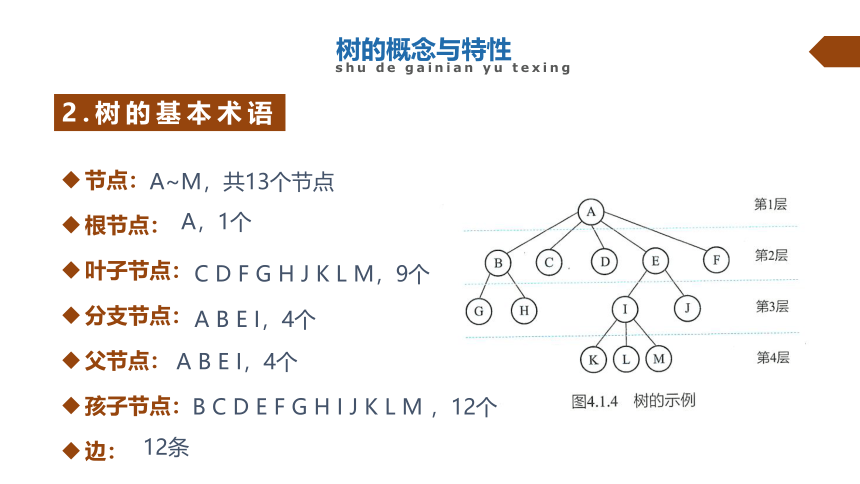
A~M,共13个节点
A,1个
C D F G H J K L M,9个
A B E I,4个
A B E I,4个
12条
B C D E F G H I J K L M ,12个
2.树的基本术语
子树:
空树:
节点的度:
树的度:
节点的层数:
树的深度:
树的概念与特性
shu de gainian yu texing
树中某个节点下面所有节点所构成的树
节点数n=0的树
树的一个节点所拥有的子树个数
节点的度中的最大值
从根开始计算,根的层数为1
节点的层数中的最大值
2.树的基本术语
子树:
空树:
节点的度:
树的度:
节点的层数:
树的深度:
树的概念与特性
shu de gainian yu texing
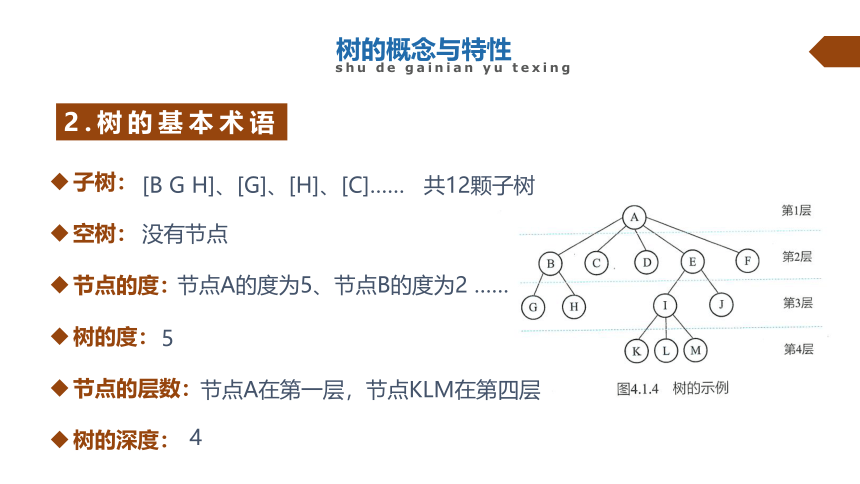
[B G H]、[G]、[H]、[C]…… 共12颗子树
没有节点
节点A的度为5、节点B的度为2 ……
5
节点A在第一层,节点KLM在第四层
4
3.树形结构特点
非线性结构:在有多个节点的树形结构中,只有一个没有前驱、只有后继的根节点,可以有多个没有后继、只有前驱的叶子节点,其余节点都只有一个直接前驱和多个直接后继
有限集合:节点个数是有限的
树的概念与特性
shu de gainian yu texing
练一练
10
9
A
3
不是
3,3
3
4
6
2
3
A
B C
I J
实践运用
猜数游戏:现在有一个100以内的正整数,请猜测这个正整数是多少,每猜测一次,都会反馈“猜大了”或者“猜小了”,直到猜出正确结果,请问猜数的策略是什么?
这个猜数策略有什么特点?
二叉树
概念
性质
满二叉树
完全二叉树
哈夫曼树
02
1.二叉树的概念
概念:是特殊的树,是一个具有n(n>=0)个节点的有限集合。
特点:①各节点的度都小于等于2
② 分为左子树和右子树,且左右子树有序
二叉树的概念
erchashu de gainian
2.二叉树的形态
二叉树的概念
erchashu de gainian
①空二叉树
(n=0)
②只有根节点的单点树
A
③只有根节点和右子树
⑤左右子树均非空
④只有根节点和左子树
练一练
请画出包含4个节点的所有形态的二叉树。
①二叉树的第k层上最多有2k-1(k>=1)个节点。
应用:
(1)如图所示,第1层上最多只有 个节点;
第2层上最多只有 个节点,以此类推,
第k层上最多只有 个节点。
二叉树的性质
erchashu de xingzhi
1
2
2k-1
②深度为k的二叉树最多有2k-1(k>=1)个节点。
应用:
根据性质①可知,第1层节点数最多为20。第2层节点数最多为21,以此类推,深度为k的二叉树节点最多有20+21+22+……+2k=2k-1
(2)某二叉树深度为3,则该二叉树最多有 个节点。
二叉树的性质
erchashu de xingzhi
7
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子结点数为n0,则n0=n2+1
应用:
如图甲,度为2的节点数为1,叶子节点数为2;
如图乙:度为2的节点数为 ,叶子节点数为 。
二叉树的性质
erchashu de xingzhi
2
3
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子结点数为n0,则n0=n2+1
二叉树的性质
erchashu de xingzhi
②深度为k的二叉树最多有2k-1(k>=1)个节点。
①二叉树的第k层上最多有2k-1(k>=1)个节点。
练一练
1、已知二叉树T共有10个节点,其中度为1的节点数量为3,则叶子节点数量为( )
A.3 B.4 C.5 D.6
B
1.满二叉树
特点:①每个节点的度为2(具有两个非空子树),或者度数为0(叶子结点)
②所有叶子节点都在同一层
特殊的二叉树
Teshu de erchashu
1.满二叉树
应用:
根据二叉树性质可知:
(1)满二叉树第k层上的节点数一定为 。
(2)一个深度为k的满二叉树一定有 个节点。
特殊的二叉树
Teshu de erchashu
2k-1
2k-1
2.完全二叉树
特点:①至多只有最下两层中的节点的度小于2
②最下一层的叶子节点都依次排列在该层最左边位置
特殊的二叉树
Teshu de erchashu
2.完全二叉树
应用:
根据二叉树性质可知:
(1)一棵深度为k的完全二叉树,第k-1层的节点个数为 。第k层的节点数 (填关系运算符) 2k-1 。
(2)已知某完全二叉树有200个节点,则该二叉树的高度为 。
特殊的二叉树
Teshu de erchashu
2k-2
<=
8
练一练
满二叉树
完全二叉树
完全二叉树
非完全二叉树
非完全二叉树
3.哈夫曼树
特殊的二叉树
Teshu de erchashu
3.哈夫曼树
特殊的二叉树
Teshu de erchashu
练一练
请从下列三棵二叉树中找到最优二叉树
①WPL=2*2+4*2+5*2+8*2=38
②WPL=4*2+5*3+8*3+2*1=49
③WPL=8*1+5*2+2*3+4*3=36
知识回顾
一个元素前面(或上面)只有一个元素,而后面(或下面)却有多个(0个或多个)元素相邻,所有的数据元素之间的特征就像一棵倒放的树。
CHZX
4.1树与二叉树
浙江省高中信息技术 选择性必修一 《数据与数据结构》
4.1.1 树
树的概念
树的基本术语
树的特性
01
1.树的概念
可以描述为由n(n>=0)个节点(Node)构成的一个有限集合以及在该集合上定义的一种节点关系。
节点:集合中的元素
树的概念与特性
shu de gainian yu texing
节点
节点
节点
节点
2.树的基本术语
树的概念与特性
shu de gainian yu texing
节点
节点
节点
节点
节点:
根节点:
叶子节点:
分支节点:
父节点:
孩子节点:
边:
集合中的元素
(开始节点)没有前驱的节点
(终端节点)度为0的节点
除叶子节点以外的节点(内部节点:除根节点之外的分支节点)
(双亲节点)对于两个以边直接连接的节点中的上端节点
连接两个节点之间的线
对于两个以边直接连接的节点中的下端节点
2.树的基本术语
树的概念与特性
shu de gainian yu texing
节点:
根节点:
叶子节点:
分支节点:
父节点:
孩子节点:
边:
A~M,共13个节点
A,1个
C D F G H J K L M,9个
A B E I,4个
A B E I,4个
12条
B C D E F G H I J K L M ,12个
2.树的基本术语
子树:
空树:
节点的度:
树的度:
节点的层数:
树的深度:
树的概念与特性
shu de gainian yu texing
树中某个节点下面所有节点所构成的树
节点数n=0的树
树的一个节点所拥有的子树个数
节点的度中的最大值
从根开始计算,根的层数为1
节点的层数中的最大值
2.树的基本术语
子树:
空树:
节点的度:
树的度:
节点的层数:
树的深度:
树的概念与特性
shu de gainian yu texing
[B G H]、[G]、[H]、[C]…… 共12颗子树
没有节点
节点A的度为5、节点B的度为2 ……
5
节点A在第一层,节点KLM在第四层
4
3.树形结构特点
非线性结构:在有多个节点的树形结构中,只有一个没有前驱、只有后继的根节点,可以有多个没有后继、只有前驱的叶子节点,其余节点都只有一个直接前驱和多个直接后继
有限集合:节点个数是有限的
树的概念与特性
shu de gainian yu texing
练一练
10
9
A
3
不是
3,3
3
4
6
2
3
A
B C
I J
实践运用
猜数游戏:现在有一个100以内的正整数,请猜测这个正整数是多少,每猜测一次,都会反馈“猜大了”或者“猜小了”,直到猜出正确结果,请问猜数的策略是什么?
这个猜数策略有什么特点?
二叉树
概念
性质
满二叉树
完全二叉树
哈夫曼树
02
1.二叉树的概念
概念:是特殊的树,是一个具有n(n>=0)个节点的有限集合。
特点:①各节点的度都小于等于2
② 分为左子树和右子树,且左右子树有序
二叉树的概念
erchashu de gainian
2.二叉树的形态
二叉树的概念
erchashu de gainian
①空二叉树
(n=0)
②只有根节点的单点树
A
③只有根节点和右子树
⑤左右子树均非空
④只有根节点和左子树
练一练
请画出包含4个节点的所有形态的二叉树。
①二叉树的第k层上最多有2k-1(k>=1)个节点。
应用:
(1)如图所示,第1层上最多只有 个节点;
第2层上最多只有 个节点,以此类推,
第k层上最多只有 个节点。
二叉树的性质
erchashu de xingzhi
1
2
2k-1
②深度为k的二叉树最多有2k-1(k>=1)个节点。
应用:
根据性质①可知,第1层节点数最多为20。第2层节点数最多为21,以此类推,深度为k的二叉树节点最多有20+21+22+……+2k=2k-1
(2)某二叉树深度为3,则该二叉树最多有 个节点。
二叉树的性质
erchashu de xingzhi
7
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子结点数为n0,则n0=n2+1
应用:
如图甲,度为2的节点数为1,叶子节点数为2;
如图乙:度为2的节点数为 ,叶子节点数为 。
二叉树的性质
erchashu de xingzhi
2
3
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子结点数为n0,则n0=n2+1
二叉树的性质
erchashu de xingzhi
②深度为k的二叉树最多有2k-1(k>=1)个节点。
①二叉树的第k层上最多有2k-1(k>=1)个节点。
练一练
1、已知二叉树T共有10个节点,其中度为1的节点数量为3,则叶子节点数量为( )
A.3 B.4 C.5 D.6
B
1.满二叉树
特点:①每个节点的度为2(具有两个非空子树),或者度数为0(叶子结点)
②所有叶子节点都在同一层
特殊的二叉树
Teshu de erchashu
1.满二叉树
应用:
根据二叉树性质可知:
(1)满二叉树第k层上的节点数一定为 。
(2)一个深度为k的满二叉树一定有 个节点。
特殊的二叉树
Teshu de erchashu
2k-1
2k-1
2.完全二叉树
特点:①至多只有最下两层中的节点的度小于2
②最下一层的叶子节点都依次排列在该层最左边位置
特殊的二叉树
Teshu de erchashu
2.完全二叉树
应用:
根据二叉树性质可知:
(1)一棵深度为k的完全二叉树,第k-1层的节点个数为 。第k层的节点数 (填关系运算符) 2k-1 。
(2)已知某完全二叉树有200个节点,则该二叉树的高度为 。
特殊的二叉树
Teshu de erchashu
2k-2
<=
8
练一练
满二叉树
完全二叉树
完全二叉树
非完全二叉树
非完全二叉树
3.哈夫曼树
特殊的二叉树
Teshu de erchashu
3.哈夫曼树
特殊的二叉树
Teshu de erchashu
练一练
请从下列三棵二叉树中找到最优二叉树
①WPL=2*2+4*2+5*2+8*2=38
②WPL=4*2+5*3+8*3+2*1=49
③WPL=8*1+5*2+2*3+4*3=36
