4.2二叉树的基本操作 课件-2021-2022学年浙教版(2019)高中信息技术选修1(25张PPT)
文档属性
| 名称 | 4.2二叉树的基本操作 课件-2021-2022学年浙教版(2019)高中信息技术选修1(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-06-04 08:34:22 | ||
图片预览





文档简介
(共25张PPT)
知识回顾
二叉树的性质:
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子结点数为n0,则n0=n2+1
②深度为k的二叉树最多有2k-1(k>=1)个节点。
①二叉树的第k层上最多有2k-1(k>=1)个节点。
知识回顾
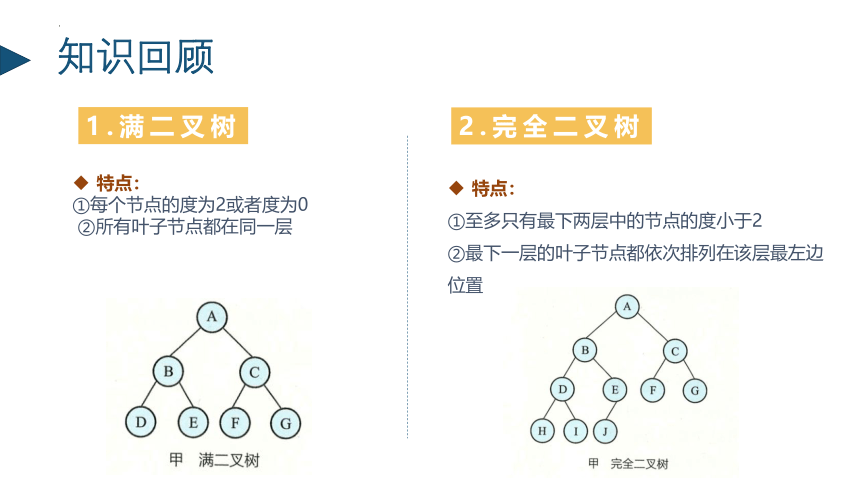
1.满二叉树
特点:
①每个节点的度为2或者度为0
②所有叶子节点都在同一层
2.完全二叉树
特点:
①至多只有最下两层中的节点的度小于2
②最下一层的叶子节点都依次排列在该层最左边位置
作业讲解
C
D
B
作业讲解
C
C
A
作业讲解
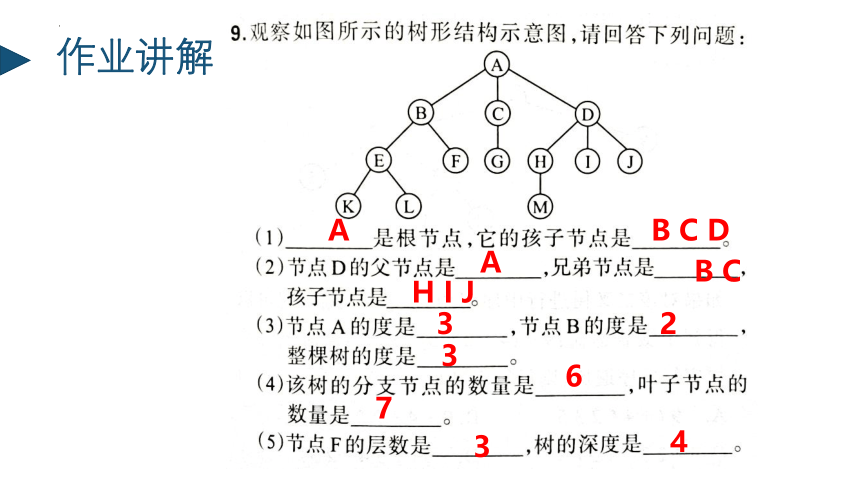
A
B C D
A
B C
H I J
3
2
3
6
7
3
4
CHZX
4.2二叉树基本操作
浙江省高中信息技术 选择性必修一 《数据与数据结构》
4.2.1 二叉树的建立
数组实现
链表实现
01
1.数组实现
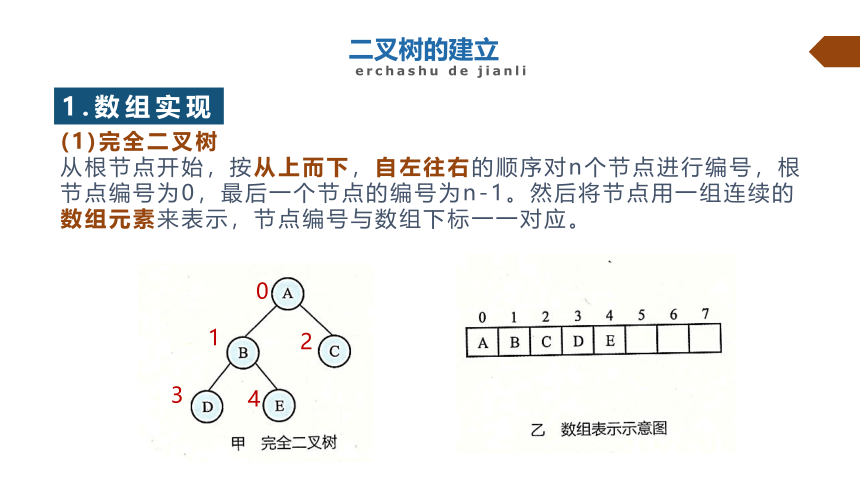
(1)完全二叉树
从根节点开始,按从上而下,自左往右的顺序对n个节点进行编号,根节点编号为0,最后一个节点的编号为n-1。然后将节点用一组连续的数组元素来表示,节点编号与数组下标一一对应。
二叉树的建立
erchashu de jianli
0
1
2
3
4
1.数组实现
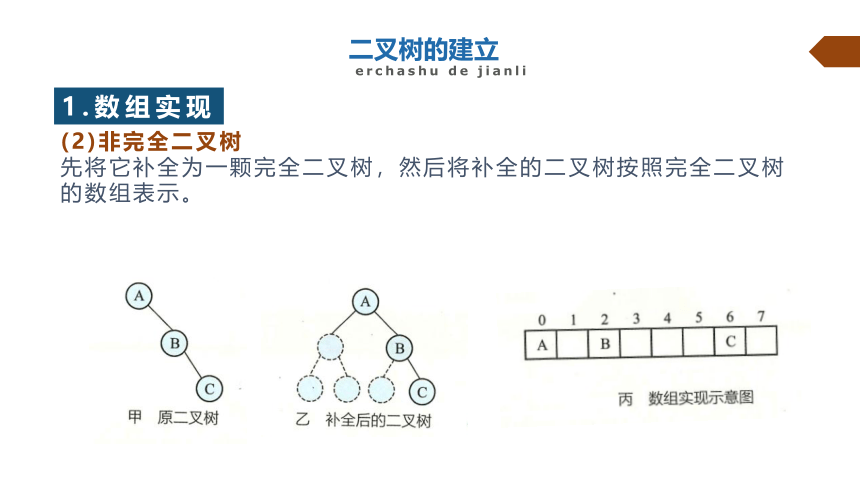
(2)非完全二叉树
先将它补全为一颗完全二叉树,然后将补全的二叉树按照完全二叉树的数组表示。
二叉树的建立
erchashu de jianli
练一练
1、某二叉树如下图所示,用数组来表示为( )
D
2.链表实现
用链表表示二叉树,至少需要3个域:一个数据域和两个指针域,两个指针域分别指向节点的左孩子和右孩子。
二叉树的建立
erchashu de jianli
3.list实现
二叉树的建立
erchashu de jianli
3.list实现
二叉树的建立
erchashu de jianli
练一练
A
二叉树的遍历
前序遍历
中序遍历
后序遍历
02
概 念:是按照一定的规则和次序访问二叉树中的所有节点,使得每个节点都被访问一次且仅被访问一次。
遍历方式:①前序遍历(根-左-右)
②中序遍历(左-根-右)
③后序遍历(左-右-根)
④层序遍历
二叉树的遍历
erchashu de bianli
1.前序遍历
规则:若二叉树为空,则空操作返回;否则,先访问根节点,再访问左子树,最后访问右子树。
二叉树的遍历
erchashu de bianli
(根左右)
2.中序遍历
规则:若二叉树为空,则空操作返回;否则,先访问左子树,再访问根节点,最后访问右子树。
二叉树的遍历
erchashu de bianli
(左根右)
3.后序遍历
规则:若二叉树为空,则空操作返回;否则,先访问左子树,再访问右子树,最后访问根节点。
二叉树的遍历
erchashu de bianli
(左右根)
4.层序遍历
规则:若二叉树为空,则空操作返回;否则,从根节点开始,自上而下,从左往右遍历。
二叉树的遍历
erchashu de bianli
练一练
则该二叉树的前序遍历序列是( )
则该二叉树的中序遍历序列是( )
则该二叉树的后序遍历序列是( )
则该二叉树的层序遍历序列是( )
a bdg cf
dgb a cf
gdb fc a
1.某二叉树如图所示:
a bc df g
练一练
则该二叉树的前序遍历序列是( )
则该二叉树的中序遍历序列是( )
则该二叉树的后序遍历序列是( )
则该二叉树的层序遍历序列是( )
A BDE CFG
DBE A GFC
DEB GFC A
2.某二叉树如图所示:
A BC DEF G
练一练
3. 一棵二叉树的前序遍历序列为“abdgecf”,中序遍历序列为“gdbeacf”,则该二叉树的后序遍历序列是( )
A.gdebfca B.gdebcfa C.gdebafc D.gedbfca
A
练一练
4、一棵二叉树的中序遍历序列为“dbgehafic”,后序遍历序列为“dghebifca”,请画出这棵二叉树,并确认是否唯一。
提示:先找到根,这样可由中序遍历得到左子树和右子树,然后再在子树中继续重复这一过程。
a
b
d
e
g
h
c
f
i
练一练
5.(多选题)已知6个节点的二叉树的前序遍历序列为ABCDEF,后序遍历序列为CBEFDA,则该二叉树的可能的中序遍历序列是( )
A. CBAEDF B. BCAFDE
C. BCAEDF D. CBAFDE
AC
知识回顾
二叉树的性质:
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子结点数为n0,则n0=n2+1
②深度为k的二叉树最多有2k-1(k>=1)个节点。
①二叉树的第k层上最多有2k-1(k>=1)个节点。
知识回顾
1.满二叉树
特点:
①每个节点的度为2或者度为0
②所有叶子节点都在同一层
2.完全二叉树
特点:
①至多只有最下两层中的节点的度小于2
②最下一层的叶子节点都依次排列在该层最左边位置
作业讲解
C
D
B
作业讲解
C
C
A
作业讲解
A
B C D
A
B C
H I J
3
2
3
6
7
3
4
CHZX
4.2二叉树基本操作
浙江省高中信息技术 选择性必修一 《数据与数据结构》
4.2.1 二叉树的建立
数组实现
链表实现
01
1.数组实现
(1)完全二叉树
从根节点开始,按从上而下,自左往右的顺序对n个节点进行编号,根节点编号为0,最后一个节点的编号为n-1。然后将节点用一组连续的数组元素来表示,节点编号与数组下标一一对应。
二叉树的建立
erchashu de jianli
0
1
2
3
4
1.数组实现
(2)非完全二叉树
先将它补全为一颗完全二叉树,然后将补全的二叉树按照完全二叉树的数组表示。
二叉树的建立
erchashu de jianli
练一练
1、某二叉树如下图所示,用数组来表示为( )
D
2.链表实现
用链表表示二叉树,至少需要3个域:一个数据域和两个指针域,两个指针域分别指向节点的左孩子和右孩子。
二叉树的建立
erchashu de jianli
3.list实现
二叉树的建立
erchashu de jianli
3.list实现
二叉树的建立
erchashu de jianli
练一练
A
二叉树的遍历
前序遍历
中序遍历
后序遍历
02
概 念:是按照一定的规则和次序访问二叉树中的所有节点,使得每个节点都被访问一次且仅被访问一次。
遍历方式:①前序遍历(根-左-右)
②中序遍历(左-根-右)
③后序遍历(左-右-根)
④层序遍历
二叉树的遍历
erchashu de bianli
1.前序遍历
规则:若二叉树为空,则空操作返回;否则,先访问根节点,再访问左子树,最后访问右子树。
二叉树的遍历
erchashu de bianli
(根左右)
2.中序遍历
规则:若二叉树为空,则空操作返回;否则,先访问左子树,再访问根节点,最后访问右子树。
二叉树的遍历
erchashu de bianli
(左根右)
3.后序遍历
规则:若二叉树为空,则空操作返回;否则,先访问左子树,再访问右子树,最后访问根节点。
二叉树的遍历
erchashu de bianli
(左右根)
4.层序遍历
规则:若二叉树为空,则空操作返回;否则,从根节点开始,自上而下,从左往右遍历。
二叉树的遍历
erchashu de bianli
练一练
则该二叉树的前序遍历序列是( )
则该二叉树的中序遍历序列是( )
则该二叉树的后序遍历序列是( )
则该二叉树的层序遍历序列是( )
a bdg cf
dgb a cf
gdb fc a
1.某二叉树如图所示:
a bc df g
练一练
则该二叉树的前序遍历序列是( )
则该二叉树的中序遍历序列是( )
则该二叉树的后序遍历序列是( )
则该二叉树的层序遍历序列是( )
A BDE CFG
DBE A GFC
DEB GFC A
2.某二叉树如图所示:
A BC DEF G
练一练
3. 一棵二叉树的前序遍历序列为“abdgecf”,中序遍历序列为“gdbeacf”,则该二叉树的后序遍历序列是( )
A.gdebfca B.gdebcfa C.gdebafc D.gedbfca
A
练一练
4、一棵二叉树的中序遍历序列为“dbgehafic”,后序遍历序列为“dghebifca”,请画出这棵二叉树,并确认是否唯一。
提示:先找到根,这样可由中序遍历得到左子树和右子树,然后再在子树中继续重复这一过程。
a
b
d
e
g
h
c
f
i
练一练
5.(多选题)已知6个节点的二叉树的前序遍历序列为ABCDEF,后序遍历序列为CBEFDA,则该二叉树的可能的中序遍历序列是( )
A. CBAEDF B. BCAFDE
C. BCAEDF D. CBAFDE
AC
