湘教版数学七年级下册 4.1.2 相交直线所成的角教案
文档属性
| 名称 | 湘教版数学七年级下册 4.1.2 相交直线所成的角教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-04 11:23:43 | ||
图片预览

文档简介
4.1.2 相交直线所成的角
【教学目标】
1.理解相交直线所成的角的意义,理解对顶角、同位角、内错角、同旁内角的概念,能准确地找出三条直线相交所构成的八个角的关系.
2.理解对顶角相等的性质.
3.会运用对顶角相等及等量代换的性质得到三条直线相交所得8个角之间的等量关系及互补关系.
【教学难点】准确找出三条直线相交所构成的八个角的关系,对顶角的性质及等量代换得到他们之间的等量关系
【教学重点】三条直线所构成的八个角的关系、对顶角的性质.
【教学内容】
一、对顶角
概念:有公共顶点,两边互为反向延长线,这样的两个角叫做对顶角.
1、你能举出生活中包含对顶角的例子吗?
2、判断下列图形中哪对∠1与∠2是对顶角?
二、探究
问题1:∠1与∠3有怎样的数量关系?比较它们的大小.
你能说出∠1=∠3的道理吗?
因为∠1与∠2互补,∠3与∠2互补(补角的定义),
所以∠1=∠3(同角的补角相等).
同理∠2=∠4.
对顶角的性质:对顶角相等.
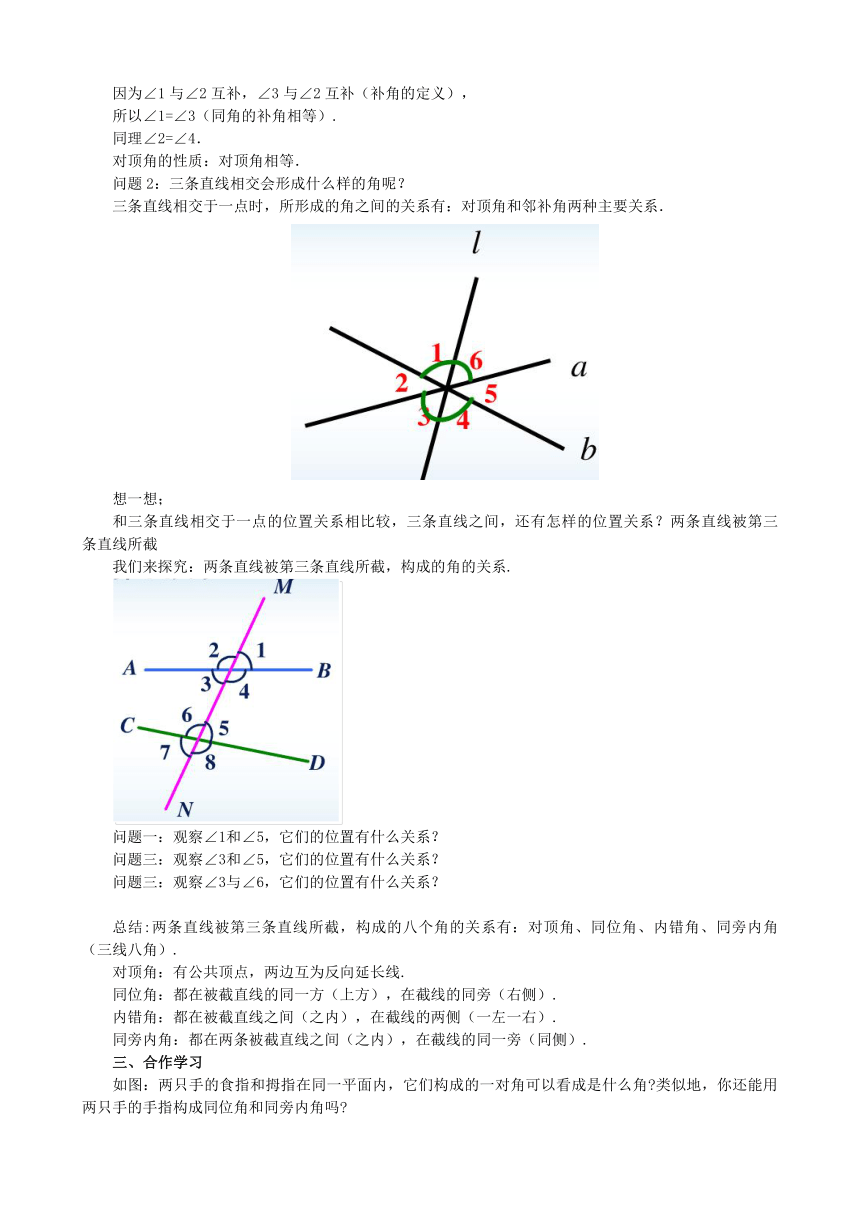
问题2:三条直线相交会形成什么样的角呢?
三条直线相交于一点时,所形成的角之间的关系有:对顶角和邻补角两种主要关系.
想一想;
和三条直线相交于一点的位置关系相比较,三条直线之间,还有怎样的位置关系?两条直线被第三条直线所截
我们来探究:两条直线被第三条直线所截,构成的角的关系.
问题一:观察∠1和∠5,它们的位置有什么关系?
问题三:观察∠3和∠5,它们的位置有什么关系?
问题三:观察∠3与∠6,它们的位置有什么关系?
总结:两条直线被第三条直线所截,构成的八个角的关系有:对顶角、同位角、内错角、同旁内角(三线八角).
对顶角:有公共顶点,两边互为反向延长线.
同位角:都在被截直线的同一方(上方),在截线的同旁(右侧).
内错角:都在被截直线之间(之内),在截线的两侧(一左一右).
同旁内角:都在两条被截直线之间(之内),在截线的同一旁(同侧).
三、合作学习
如图:两只手的食指和拇指在同一平面内,它们构成的一对角可以看成是什么角 类似地,你还能用两只手的手指构成同位角和同旁内角吗
四、动脑筋:考考你的眼力
如图,三条直线有怎样的位置关系?三条直线两两相交所形成的12个角之间有哪些位置关系?
五、例题讲解
例1 如图,直线EF与AB,CD相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4, ∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2 如图,直线CD,EF被直线AB所截.
1、如果∠1=∠4,那么∠3与∠6相等吗? ∠1与∠2相等吗?∠1与∠3互补吗?
2、如果∠1=∠2,那么∠3与∠7相等吗? ∠1与∠4相等吗?∠1与∠3互补吗?
3、如果∠1与∠3互补,那么∠2与∠7也互补吗?∠1与∠4相等吗?∠1与∠2相等吗?
深化概念,提升能力
1、如果两条直线被第三条直线所截有一组同位角相等,那么其他的同位角也相等,内错角也相等,同旁内角互补.
2、如果两条直线被第三条直线所截有一组内错角相等,那么另外一组内错角也相等,同位角相等,同旁内角互补.
3、如果两条直线被第三条直线所截有一组同旁内角互补,那么另外一组同旁内角也互补,同位角相等,内错角相等.
例3 如图,直线a,b被直线c所截,找出图中所有的同位角、内错角、同旁内角.设∠1=∠4=108°,求其他角的度数.
解:∠1与∠4,∠2与∠5是同位角;∠3与∠4是内错角;∠2与∠4是同旁内角.
因有一对同位角相等,即∠1=∠4=108°,
所以∠3=∠4=108°,∠2 = 180°-∠1 = 72°,∠5 = 180°-∠4 = 72°.
六、课堂小结
1.你能总结一下对顶角、同位角、内错角、同旁内角分别具有哪些特征吗?
2.你认为在图形中识别对顶角、同位角、内错角、同旁内角的关键是什么?
3.对顶角一定相等;同位角、内错角、同旁内角之间一定具有什么数量关系吗?
1
2
3
4
8
7
6
5
A
B
C
D
E
F
【教学目标】
1.理解相交直线所成的角的意义,理解对顶角、同位角、内错角、同旁内角的概念,能准确地找出三条直线相交所构成的八个角的关系.
2.理解对顶角相等的性质.
3.会运用对顶角相等及等量代换的性质得到三条直线相交所得8个角之间的等量关系及互补关系.
【教学难点】准确找出三条直线相交所构成的八个角的关系,对顶角的性质及等量代换得到他们之间的等量关系
【教学重点】三条直线所构成的八个角的关系、对顶角的性质.
【教学内容】
一、对顶角
概念:有公共顶点,两边互为反向延长线,这样的两个角叫做对顶角.
1、你能举出生活中包含对顶角的例子吗?
2、判断下列图形中哪对∠1与∠2是对顶角?
二、探究
问题1:∠1与∠3有怎样的数量关系?比较它们的大小.
你能说出∠1=∠3的道理吗?
因为∠1与∠2互补,∠3与∠2互补(补角的定义),
所以∠1=∠3(同角的补角相等).
同理∠2=∠4.
对顶角的性质:对顶角相等.
问题2:三条直线相交会形成什么样的角呢?
三条直线相交于一点时,所形成的角之间的关系有:对顶角和邻补角两种主要关系.
想一想;
和三条直线相交于一点的位置关系相比较,三条直线之间,还有怎样的位置关系?两条直线被第三条直线所截
我们来探究:两条直线被第三条直线所截,构成的角的关系.
问题一:观察∠1和∠5,它们的位置有什么关系?
问题三:观察∠3和∠5,它们的位置有什么关系?
问题三:观察∠3与∠6,它们的位置有什么关系?
总结:两条直线被第三条直线所截,构成的八个角的关系有:对顶角、同位角、内错角、同旁内角(三线八角).
对顶角:有公共顶点,两边互为反向延长线.
同位角:都在被截直线的同一方(上方),在截线的同旁(右侧).
内错角:都在被截直线之间(之内),在截线的两侧(一左一右).
同旁内角:都在两条被截直线之间(之内),在截线的同一旁(同侧).
三、合作学习
如图:两只手的食指和拇指在同一平面内,它们构成的一对角可以看成是什么角 类似地,你还能用两只手的手指构成同位角和同旁内角吗
四、动脑筋:考考你的眼力
如图,三条直线有怎样的位置关系?三条直线两两相交所形成的12个角之间有哪些位置关系?
五、例题讲解
例1 如图,直线EF与AB,CD相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4, ∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2 如图,直线CD,EF被直线AB所截.
1、如果∠1=∠4,那么∠3与∠6相等吗? ∠1与∠2相等吗?∠1与∠3互补吗?
2、如果∠1=∠2,那么∠3与∠7相等吗? ∠1与∠4相等吗?∠1与∠3互补吗?
3、如果∠1与∠3互补,那么∠2与∠7也互补吗?∠1与∠4相等吗?∠1与∠2相等吗?
深化概念,提升能力
1、如果两条直线被第三条直线所截有一组同位角相等,那么其他的同位角也相等,内错角也相等,同旁内角互补.
2、如果两条直线被第三条直线所截有一组内错角相等,那么另外一组内错角也相等,同位角相等,同旁内角互补.
3、如果两条直线被第三条直线所截有一组同旁内角互补,那么另外一组同旁内角也互补,同位角相等,内错角相等.
例3 如图,直线a,b被直线c所截,找出图中所有的同位角、内错角、同旁内角.设∠1=∠4=108°,求其他角的度数.
解:∠1与∠4,∠2与∠5是同位角;∠3与∠4是内错角;∠2与∠4是同旁内角.
因有一对同位角相等,即∠1=∠4=108°,
所以∠3=∠4=108°,∠2 = 180°-∠1 = 72°,∠5 = 180°-∠4 = 72°.
六、课堂小结
1.你能总结一下对顶角、同位角、内错角、同旁内角分别具有哪些特征吗?
2.你认为在图形中识别对顶角、同位角、内错角、同旁内角的关键是什么?
3.对顶角一定相等;同位角、内错角、同旁内角之间一定具有什么数量关系吗?
1
2
3
4
8
7
6
5
A
B
C
D
E
F
